2208.07339_LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale¶
组织: University of Washington, Facebook AI Research, Hugging Face, ENS Paris-Saclay
相关参考¶
Abstract¶
大语言模型通常需要大量GPU内存进行推理。为了解决这个问题,研究人员提出了一种叫做 LLM.int8() 的方法,把模型中的部分矩阵计算从16/32位压缩成 8位整数,内存占用减半,但精度几乎不变。
具体做法是:
大多数特征用一种“逐向量量化”方式处理;
对少数重要但难以压缩的“异常特征”,用一种混合精度方法(保留16位)来处理。
这个方法可以让像175B参数的超大模型(如OPT-175B/BLOOM)在一台配有消费级GPU的服务器上运行,而不会影响模型性能。
其他
有两个 Pitch。
一个 Pitch 是关于我如何使用先进的量化方法,实现规模化、无性能损失的 Transformer 推理,从而使大型模型更容易上手。
另一个 Pitch 讨论了 Transformer 中涌现的异常值,以及它们如何彻底改变 Transformer 的学习内容和运作方式。
量化研究就像打印机。
没人关心打印机,也没人喜欢打印机。
但如果打印机能正常工作,每个人都会很高兴。
1. Introduction¶
🌟背景问题:¶
大型语言模型(如GPT-3)参数量巨大,推理时消耗大量内存和计算资源。
Transformer 模型中 95% 的参数 和 65-85%计算量 来自前馈层和注意力投影层。
为了减小内存使用,研究者尝试用 8位量化(即用更少的比特表示权重),但:
往往会降低模型性能;
以前的方法只能处理 小于 3.5 亿参数 的模型;
对于数十亿参数的大模型,量化仍是个挑战。
🧠这篇论文的核心贡献:¶
提出了一种新的量化方法 LLM.int8(),可在 不损失性能的前提下,把 高达175B参数的模型 的主要计算部分(前馈层和注意力层)转换为 8位精度,且不损失模型性能,直接可用于推理。
🧠两大技术难点:
大模型需要更高的量化精度(>1B 参数时常规精度不够)
大模型中会出现极少但影响极大的“离群特征”,特别是在参数量超过 6.7B 时,这些特征严重干扰量化精度。
🛠解决方法分为两步:
向量级量化(Vector-wise Quantization):
矩阵乘法可以看作是一系列独立的行向量和列向量的内积
分别对每个内积单独归一化,提高量化精度;
在执行下一个运算之前,我们可以利用列向量和行向量归一化常数的外积进行反归一化,从而恢复矩阵乘法的输出
可在参数量 ≤2.7B 时保持模型性能。
混合精度处理离群特征(Mixed-Precision for Outliers):
分析发现:6.7B 参数后,隐藏状态中会出现极大值离群特征,集中在 6 个特征维度;
解决办法:对这极少的离群维度使用 16 位乘法,其余 99.9% 的维度仍使用 8 位乘法;
这样既保留精度,也节省内存和计算。
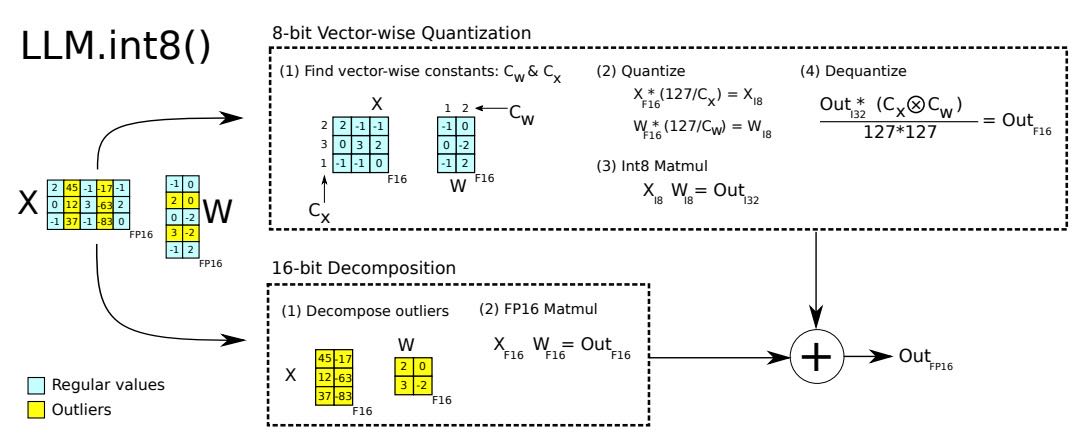
Figure 2 illustrates the workflow of LLM.int8(). Given 16-bit floating-point inputs \(\mathbf{X}{f16}\) and weights \(\mathbf{W}{f16}\), the features and weights are first decomposed into sub-matrices: one for large-magnitude (outlier) features and another for all remaining values. The outlier matrices are processed using standard 16-bit matrix multiplication to preserve precision. For the remaining values, 8-bit vector-wise quantization is applied. This involves computing the row-wise and column-wise absolute maximums, denoted as \(\mathbf{C}_x\) and \(\mathbf{C}w\), which are used to scale (normalize) the input and weight matrices. These scaled values are then quantized to Int8 and used in Int8 matrix multiplication, resulting in Int32 outputs \(\mathbf{Out}{i32}\). These outputs are then dequantized using the outer product of the normalization constants, \(\mathbf{C}_x \otimes \mathbf{C}_w\). Finally, both the 16-bit results from the outlier paths and the dequantized results from the 8-bit paths are accumulated into 16-bit floating-point outputs.
🔍离群特征的影响:¶
虽然只占 0.1% 的特征,但对模型输出影响极大;
去掉这些特征会使注意力的 softmax 结果下降 20%+,验证集困惑度(perplexity)恶化 600%-1000%;
而随机去掉同样数量的普通特征,影响几乎可以忽略。
备注
总结:这项工作成功在不损失精度的前提下,将超大模型量化为 8 位精度,可显著降低部署成本,并首次让如 OPT-175B 等模型可在单个消费级 GPU 服务器上运行。
📊实验证明:¶
LLM.int8() 保持了与 16位原模型相同的精度;
在 OPT、GPT-3、BLOOM 等大模型上测试表现优异;
可在消费级显卡上部署 175B 规模模型;
推理速度也没有变慢。
2. Background¶
📌 研究目的:¶
本文研究在大模型(Transformer)中,量化技术(quantization)在什么规模下会失效,以及失败的原因与精度之间的关系。
对比两种常用的 8bit 量化方法:对称量化(Absmax)和非对称量化(Zeropoint)。
🔹 1. absmax(对称量化)¶
absmax: absolute maximum quantization
将整个张量的最大绝对值设为127,缩放所有值进8bit范围 [-127, 127]。
算法简单,硬件友好,是目前使用最广的方法。
缺点:如果输入数据分布偏向一侧(如ReLU输出都是正数),会浪费一半的数值范围。
🔹 2. zeropoint(非对称量化)¶
zeropoint: Zeropoint Quantization
用缩放因子(ndx)加上偏移值(zeropoint zp)来线性映射整个张量,使其充分利用 [-127,127] 整个范围。
优点:更高精度,特别适合非对称数据(如ReLU输出)。
缺点:实现复杂,需要额外的计算,比如加上 zeropoint,通常比 absmax 慢,尤其是在没有专用指令的硬件上(如 GPU/TPU)。
说明
零点量化分为两步
第一步值域映射,即通过缩放将原始的数值范围映射为量化后的数值范围
第二步零点调整,即通过平移将映射后的数据的最小值对齐为目标值域的最小值
具体 zeropoint 参见 0normal
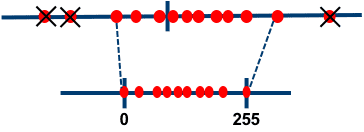
from: 这儿
示例¶
假设你要用 absmax 对向量 [1.2, -0.5, -4.3, 1.2, -3.1, 0.8, 2.4, 5.4] 进行量化。
首先需要计算该向量元素的最大绝对值,在本例中为 5.4。
Int8 的范围为 [-127, 127],因此我们将 127 除以 5.4,得到缩放因子 23.5。
最后,将原始向量乘以缩放因子得到最终的量化向量 [28, -12, -101, 28, -73, 19, 56, 127]。
要恢复原向量,可以将 int8 量化值除以缩放因子,但由于上面的过程是“四舍五入”的,我们将丢失一些精度。
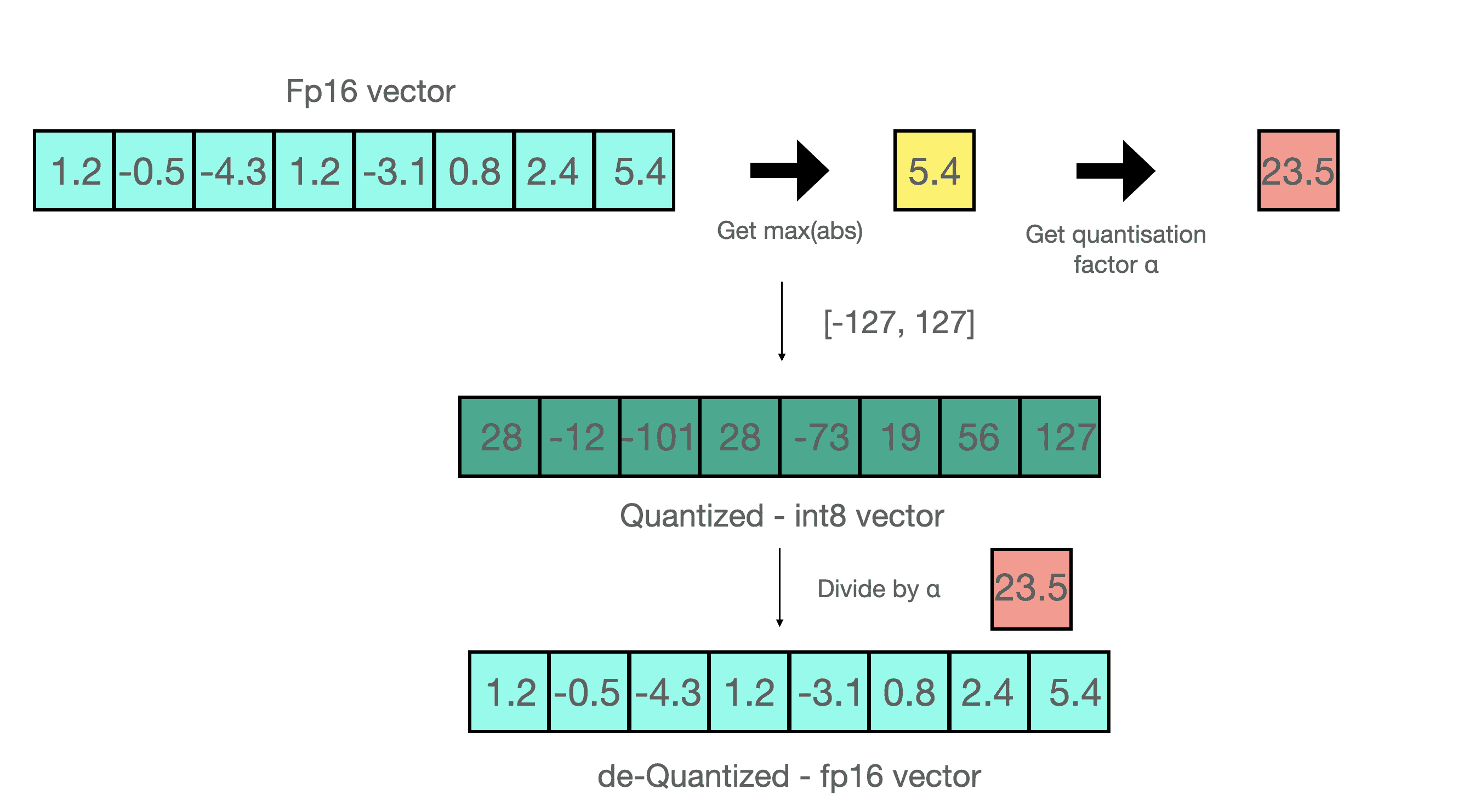
对于无符号 Int8,我们可以先减去最小值然后再用最大绝对值来缩放,这与零点量化的做法相似。
其做法也与最小 - 最大缩放 (min-max scaling) 类似,但后者在缩放时会额外保证输入中的 0 始终映射到一个整数,从而保证 0 的量化是无误差的。
🧮 矩阵乘法中的使用方式¶
先把输入(X)和权重(W)从 16-bit 浮点量化为 8-bit 整数。
然后在 Int8/Int16/Int32 上做乘法和加法。
最后用缩放因子把结果还原(dequantize)为 16-bit 浮点。
🧠 核心结论预示:¶
量化策略的效果随着模型规模可能会变化。
虽然 absmax 更易部署,但在大模型中可能需要考虑 zeropoint 以提高精度。
研究的重点是理解这两种量化在不同模型规模下的适用性。
3. Int8 Matrix Multiplication at Scale¶
🌟核心问题¶
传统量化方法(例如一个张量用一个缩放因子)在遇到少量异常值(outliers) 时,会严重影响整体精度。
✅解决方案:LLM.int8() 方法¶
向量级量化(Vector-wise Quantization)
不再使用单一缩放因子,而是:
每行输入矩阵用一个缩放因子
每列权重矩阵用一个缩放因子
这样可以更细粒度地控制缩放,提升量化精度。
混合精度分解(Mixed-precision Decomposition)
对于非常稀有但数值大的特征维度(< 0.1%),仍使用16-bit精度
其余99.9%的维度使用8-bit进行乘法计算
这样既保留精度,又节省内存(约减少50%)
📊实验¶
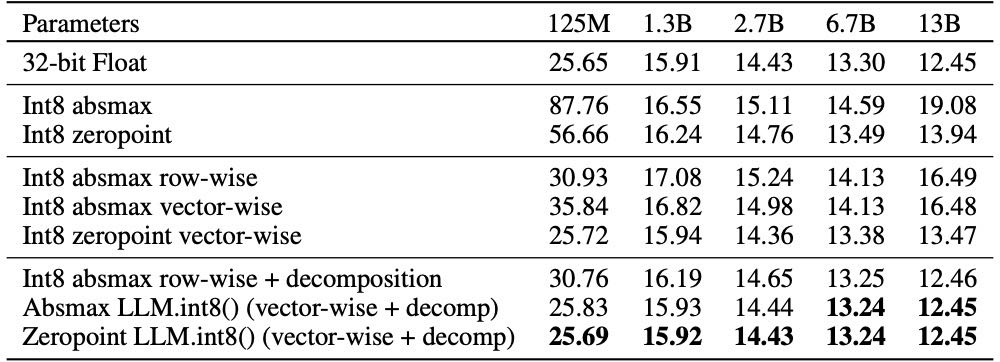
Table 1: 对不同 Transformer 模型规模(从 125M 到 13B) 使用不同 量化方法 后的效果比较,使用的是 C4 验证集的 perplexity 作为衡量指标
在 Transformer 模型参数规模从 125M 扩展到 13B 时,普通的 Int8 量化策略(如 absmax、row-wise、zeropoint)会因无法表示大幅 outlier 特征而导致显著的性能下降。尤其在 13B 模型中,量化后的 perplexity 甚至比更小的 6.7B 模型还差。相比之下,LLM.int8() 使用混合精度方法,仅用极少数 Float16 维度表达 outlier,其余维度采用 Int8,从而在保持计算效率的同时,完全恢复了原始模型的 perplexity。这证明了该方法在大模型量化中的可扩展性与有效性。
125M量化后性能下降大的原因:125M 参数规模的模型表达能力有限,每一位精度的损失对整体性能影响更大。大模型(如 6.7B、13B)虽然有更多 outlier,也更难量化,但它们冗余度高,量化时丢点精度,模型可以自我弥补。小模型(如125M)本身冗余少、容错低、表达能力弱,所以即便量化中 outlier 不多,也因整体量化误差比例较大、抗干扰能力差而出现更大的性能下降。
实验设置:
在多个大模型(125M ~ 175B参数)上评估方法效果
指标包括语言建模困惑度(Perplexity)和Zero-shot表现
结果:
传统方法效果随模型变大而急剧下降
LLM.int8() 是唯一能随着模型规模扩展仍保持性能的方法
总结¶
LLM.int8() = 向量级量化 + 混合精度分解
能大幅节省内存(最大约1.96x)
是目前唯一在大模型上仍保持准确性的8-bit量化方法
推理速度:
与 FP16 基准相比
对于参数少于 67 亿的模型,量化开销可能会降低推理速度。
对于相当于 1750 亿模型的大型矩阵乘法,LLM.int8() 的运行时间大约快两倍。
4. Emergent Large Magnitude Features in Transformers at Scale¶
定义-什么是“Outlier Feature”?¶
Transformer 模型中的中间表示(hidden state)是一个二维张量: \(\mathbf{X} \in \mathbb{R}^{s \times h}\)
其中:
\(s\):序列长度(tokens 数量)
\(h\):特征维度(每个 token 的隐藏向量维度)
“Outlier Feature” 指的是:在某一维度 \(h_i\) 上,它的值非常大(比如绝对值 ≥ 6),而且:
出现在至少 25% 的 Transformer 层(比如有 100 层,有 25 层该维度上有这种大值)
并且在至少 6% 的 token(序列维度) 上都出现过
也就是说,这是一个 非常显著、跨层一致出现的异常特征维度。
说明¶
随着 Transformer 模型规模增大,会出现一些 特征维度上的“异常值”(magnitude 很大),它们:
影响范围广:出现在几乎所有层、影响大部分 token。
数量虽多但集中:例如一个 13B 参数的模型中,2048 token 的序列可能有 15 万个异常值,但它们只集中在最多 7 个特征维度。
这些 Outlier Feature 是怎么出现的?¶
研究发现:模型参数越大,这种 Outlier Feature 就越容易出现,幅度也越大。这种现象被称为“涌现”(emergence)。
有两种分析方式:
从模型规模来看(参数量):
6B 参数前后,突然开始出现异常值
比如模型从 6B 到 6.7B,出现 outlier 的层数从 65% → 100%
对应 token 的数量从 35% → 75%
这是一个相当剧烈的跃迁 → 类似物理中的“相变”
从模型效果来看(perplexity):
Perplexity 越低(模型性能越好),outlier 出现得越多
但这个过程是平滑变化的,不像参数量那样突然
结论:outlier 的出现既与参数量相关,也与训练质量(如数据量、数据好坏)相关。
为什么 Outlier 会带来问题?¶
对模型性能影响:
这些 Outlier 特征 极度重要,即使只有 6~7 个特征维度:
若你把这些维度设为 0,top-1 准确率从 40% 降到 20%
验证集 perplexity 增加 600%-1000%
说明模型强烈依赖这些特征
对量化的影响(尤其 Int8):
常规的 Int8 量化(如 row-wise 或 vector-wise):
假设每一行单独缩放,但 outlier 是列方向的(即维度方向 h)
导致很多值都被“挤压”在一起,小值变 0,大值保不住 → 丢失信息
尤其 Int8 的动态范围有限(−127,127)
outlier 的存在会撑爆分布,造成其他正常值精度下降
例如当值达到 60,再乘一个矩阵,很容易超出 Int16/Float16 的最大表示范围(65535)
即使是对称量化(如 row-wise/vector-wise)也难以处理这些异常值,因为它们出现在 feature 维度,不是序列维度。
应对方法:¶
Zeropoint 量化(非对称)
一种非对称量化方法,可以对偏移值做补偿
适合 outlier 的分布(outlier 往往是正或负,不是对称分布)
可以缓解一些问题
LLM.int8() 提出的 Mixed-Precision Decomposition 方法:
把隐藏状态分成:
主体部分(用 Int8)
Outlier 特征部分(保留为 Float16)
只用极少量的浮点数(比如保留 6 个维度),就能恢复全部精度
效果好得多,而且极大节省内存和算力
示例¶
假设你有一个 Transformer,每一层的某一维度(如第 1234 维)突然在很多 token 上值变成了 60(正常值可能是 -1 到 1 之间),这时:
如果你直接做 Int8 量化:
你得为这个 60 留出空间
导致其他绝大多数的小值(比如 0.2)会被量化成 0,信息丢失
如果你用混合精度处理:
把第 1234 维单独提出来,用 Float16 表示
其他维度还是 Int8,就能保住精度又节省计算

LLM.int8() 通过三个步骤完成矩阵乘法计算:
从输入的隐含状态中,按列提取异常值 (即大于某个阈值的值)。
对 FP16 离群值矩阵和 Int8 非离群值矩阵分别作矩阵乘法。
反量化非离群值的矩阵乘结果并其与离群值矩阵乘结果相加,获得最终的 FP16 结果。
6. Discussion and Limitations¶
我们首次证明了:超大参数量(比如 175B)的 Transformer 模型可以量化为 Int8,并在推理时几乎不损失性能。方法是:
关键做法:用混合精度(把特异值分离出来用16位计算)+ 向量级量化,得到一种叫 LLM.int8() 的方法。
结果:这个方法可以保持模型原有的推理能力。
局限性有四点:
只研究了 Int8,没有研究 FP8(因为硬件支持不足)。
只测试了最多 175B 参数的模型,更大的模型可能出现无法预料的新问题。
注意力机制没用 Int8,因为它不涉及权重参数,也暂时没必要。
只研究了推理,没有深入研究训练或微调(训练时的精度、速度和平衡问题更复杂,留待以后探索)。
7. Broader Impacts¶
我们的工作让原本因显存不足而无法使用的大模型现在可以在GPU上运行,这对资源有限的研究者尤其有帮助。同时,也让资源丰富的机构能在相同GPU上运行更多模型,可能加大资源差距。
我们认为,结合我们提出的 Int8 推理方法和一些公开的大模型(如 OPT),将使学术界在零样本/少样本任务上开展新的研究。这种模型普及对社会可能带来正面和负面影响,尚难预测。
其他¶
将所有 nn.Linear 模块替换为 bnb.nn.Linear8bitLt 而无需占用内存:¶
# 放弃了对某些模块 (这里时 lm_head) 进行替换,因为我们希望保持输出层的原始精度以获得更精确、更稳定的结果
# 将 has_fp16_weights 属性设置为 False,以便直接将权重加载为 Int8,并同时加载其量化统计信息
def replace_8bit_linear(model, threshold=6.0, module_to_not_convert="lm_head"):
for name, module in model.named_children():
if len(list(module.children())) > 0:
replace_8bit_linear(module, threshold, module_to_not_convert)
if isinstance(module, nn.Linear) and name != module_to_not_convert:
with init_empty_weights():
model._modules[name] = bnb.nn.Linear8bitLt(
module.in_features,
module.out_features,
module.bias is not None,
has_fp16_weights=False,
threshold=threshold,
)
return model
示例¶
导入模块
import torch
import torch.nn as nn
import bitsandbytes as bnb
from bnb.nn import Linear8bitLt
定义自己的模型&训练&保存模型
fp16_model = nn.Sequential(
nn.Linear(64, 64),
nn.Linear(64, 64)
)
# [... train the model ...]
torch.save(fp16_model.state_dict(), "model.pt")
定义一个 int8 模型
int8_model = nn.Sequential(
Linear8bitLt(64, 64, has_fp16_weights=False),
Linear8bitLt(64, 64, has_fp16_weights=False)
)
加载 8 位模型(在设计上采用 延迟量化(delayed quantization) 机制)
int8_model.load_state_dict(torch.load("model.pt"))
int8_model = int8_model.to(0) # 量化发生在此处
在调用 .to 函数之前打印 int8_model[0].weight:
int8_model[0].weight
Parameter containing:
tensor([[ 0.0031, -0.0438, 0.0494, ..., -0.0046, -0.0410, 0.0436],
[-0.1013, 0.0394, 0.0787, ..., 0.0986, 0.0595, 0.0162],
[-0.0859, -0.1227, -0.1209, ..., 0.1158, 0.0186, -0.0530],
...,
[ 0.0804, 0.0725, 0.0638, ..., -0.0487, -0.0524, -0.1076],
[-0.0200, -0.0406, 0.0663, ..., 0.0123, 0.0551, -0.0121],
[-0.0041, 0.0865, -0.0013, ..., -0.0427, -0.0764, 0.1189]],
dtype=torch.float16)
在调用 .to 函数之后打印 int8_model[0].weight:
int8_model[0].weight
Parameter containing:
tensor([[ 3, -47, 54, ..., -5, -44, 47],
[-104, 40, 81, ..., 101, 61, 17],
[ -89, -127, -125, ..., 120, 19, -55],
...,
[ 82, 74, 65, ..., -49, -53, -109],
[ -21, -42, 68, ..., 13, 57, -12],
[ -4, 88, -1, ..., -43, -78, 121]],
device='cuda:0', dtype=torch.int8, requires_grad=True)
反量化获取 FP16 权重
# CB:原始 int8 权重,例如范围是 [-127, 127] 的整数矩阵
# SCB:scale 因子,即每个通道/块的缩放比例
(int8_model[0].weight.CB * int8_model[0].weight.SCB) / 127