主页

索引

模块索引

搜索页面

2502.20653_Dataset Distillation with Neural Characteristic Function: A Minmax Perspective

• https://arxiv.org/abs/2502.20653

• Label: 数据蒸馏

Abstract

• 数据集蒸馏是一种减少深度学习数据需求的有效方法，分布匹配方法在计算效率和性能上表现突出。

• 现有的分布匹配距离度量常常无法准确捕捉分布差异，导致不可靠的差异度量。

• 本文将数据集蒸馏重新表述为一个最小最大优化问题，提出了神经特征函数差异（NCFD, Neural Characteristic Function Discrepancy）作为一种全面且理论基础扎实的度量。

• NCFD利用特征函数（CF）捕捉完整的分布信息，通过神经网络优化CF频率参数的采样策略，最大化差异以增强距离估计。

• 提出的神经特征函数匹配（NCFM, Neural Characteristic Function Matching）方法在复杂平面中对真实和合成数据的神经特征相位和幅度进行对齐，实现合成样本的真实感和多样性平衡。

• 实验表明，该方法在低分辨率和高分辨率数据集上显著优于现有方法，ImageSquawk上准确率提升20.5%。

• 方法在GPU内存使用上减少超过300倍，处理速度比现有方法快20倍。

• 这是首次在单个NVIDIA 2080 Ti GPU上使用仅2.3 GB内存实现CIFAR-100的无损压缩。

1. Introduction

• 深度神经网络（DNN）在多任务上取得显著进展，但有限数据训练仍具挑战性。

• 数据集蒸馏被提出以将大规模真实数据集浓缩为小型合成数据集，适用于神经架构搜索、持续学习、医学图像计算和隐私保护等领域。

• 特征或分布匹配（DM）方法在数据集蒸馏中因其高效性和性能平衡而受到欢迎。

• DM方法相比于双层优化的蒸馏方法，省去了嵌套优化的需求，计算时间仅为后者的十分之一，同时在 CIFAR-10 数据集上以每类50张图像的情况下，测试准确率更高。

• DM中的关键挑战是有效度量真实与合成数据集之间的分布差异。

• 早期方法使用均方误差（MSE）比较特征，但未能捕捉高维流形中的语义结构。

• 后来的方法采用最大均值差异（MMD, Maximum Mean Discrepancy）作为度量，能在潜在希尔伯特空间中对分布的矩进行对齐。

• 然而，仅对齐矩并不保证完全的分布匹配，MMD方法可能导致合成图像质量不佳。

• 提出了一种新方法，将分布匹配重构为对抗性最小最大优化问题，动态学习差异度量，提升真实与合成数据分布的可分性。

• 引入神经特征差异（NCFD），基于特征函数（CF）提供精确的概率分布表示，具有线性时间复杂度。

• 神经特征函数匹配（NCFM）对真实与合成数据的神经特征在复平面上进行相位和幅度对齐，实现真实感与多样性的平衡。

• 在多个基准数据集上进行广泛实验，NCFM在高分辨率数据集上显著提高准确率，GPU内存使用减少300倍，支持在单个NVIDIA 2080 Ti GPU上进行无损数据集蒸馏。

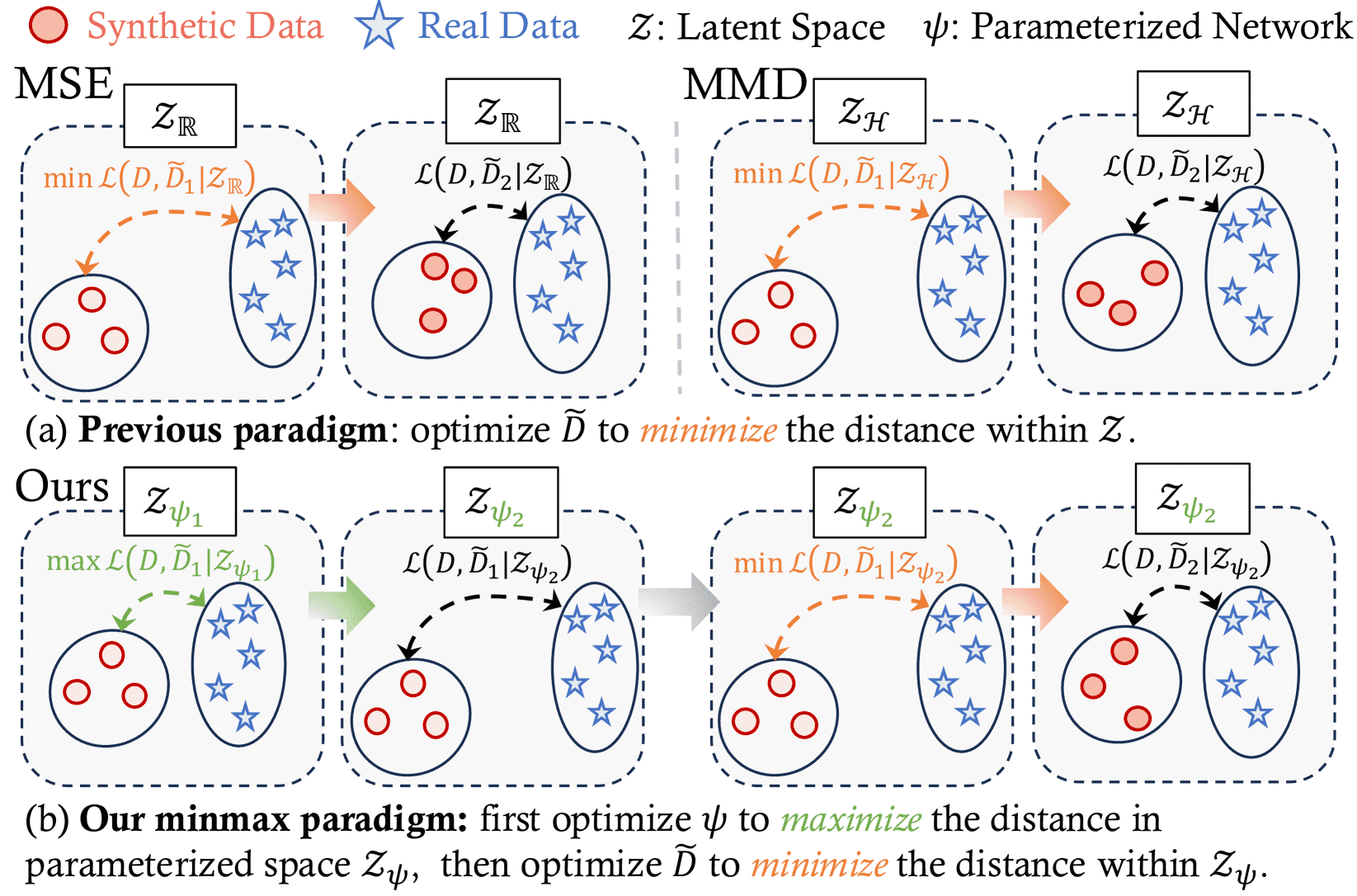
Figure 1: Comparison of different paradigms for dataset distillation. (a) The MSE approach compares point-wise features within Euclidean space, denoted as $\mathcal{Z}\mathrm{\_}\mathbb{R}$ , while MMD evaluates moment differences in Hilbert space, $\mathcal{Z}\mathrm{\_}\mathcal{H}$ . (b) Our method redefines distribution matching as a minmax optimization problem, where the distributional discrepancy is parameterized by a neural network $\psi$ . We begin by optimizing $\psi$ to maximize the discrepancy, thereby establishing the latent space $\mathcal{Z}\mathrm{\_}\psi$ , and subsequently optimize the synthesized data $\tilde{\mathcal{D}}$ to minimize this discrepancy within $\mathcal{Z}\mathrm{\_}\psi$ .

Figure 2: Comparison of different distribution matching methods. (a) Illustration of embedded features from the real domain to complex-plane features using Euler’s formula. The latent neural feature $Phi_{bm{x}}(bm{t})$ captures the amplitude and phase information. (b) MMD-based methods align feature moments in the embedded domain but may not effectively align the overall distributions. (c) CF-based methods directly compare distributions by balancing the amplitude and phase in the complex plane, enhancing distributional similarity.

2. Related Work

• 数据集蒸馏方法分为点对点匹配和时刻匹配，DM方法在性能和计算效率上表现优越，避免了嵌套模型优化。

• 时刻匹配方法通过最小化合成数据与真实数据之间的最大均值差异（MMD）来进行。

• 点对点特征匹配则通过改进卷积神经网络中提取的特征匹配策略来提升性能。

• 现有的匹配方法可能无法充分捕捉合成数据与真实数据之间的整体分布差异。

• 特征函数（CF）作为一种分布度量，能够完全定义概率分布，提供了一种替代的分析方法。

• CF在深度学习中的生成建模任务中已有应用，但尚未用于数据蒸馏。

7. Conclusion

• 将数据集蒸馏中的分布匹配重新定义为最小最大优化问题。

• 提出了神经特征函数差异（NCFD），旨在最大化真实数据与合成数据的可分性。

• 利用特征函数（CF）动态调整NCFD，以平衡复平面中的相位和幅度信息。

• 实验表明该方法计算效率高，具有最小计算开销，适用于大规模应用。

主页

索引

模块索引

搜索页面