实用密码学¶
目录
范学雷,在密码学应用领域已经工作了二十多年了。目前,担任 Oracle 的首席软件工程师,是 Java 安全组的成员,OpenJDK 安全评审成员,也是 Java 安全的主要推动者和贡献者之一。
CPB: Cycles Per Byte(每字节周期数)
CBC: Cipher Block Chaining
密码学 101
BEAST attack
00开篇词 _ 人人都要会点密码学¶
经典书籍:Bruce Schneier 的《应用密码学:协议、算法与 C 源程序》
安全工程师是一个很大的门类,比如说,防火墙、病毒、安全漏洞、密码学等等。密码学是其中的一个方向。
01 | 学习密码学有什么用¶
信息安全的六个需求:
需求一:识别身份,确定发送方
需求二:认证身份,验证发送方
需求三:管理特权,授予接收方查看信息权利
需求四:信息保密,没有权限不能查看信息
需求五:信息完整,保护内容不被篡改
需求六:信息可用,保持信息获取能力
授权的过程:
* 身份标识(Identification)
* 身份认证(Authentication)
* 授权(Authorization)
解决了权限管理的基本问题:
该怎么标识身份?
该怎么验证身份?
以及一个身份拥有什么样的权利?
安全的要素:
* 机密性(Confidentiality)
* 完整性(Integrity)
* 可用性(Availability)
解决了信息安全的基本问题:
信息怎么能够完整地、
秘密地传递出去、
接收进来?
机密性和完整性可以由密码套件来保障(TLS_ECDHE_RSA_WITH_AES_128_GCM_SHA256)
身份验证需要有 PKI(公钥基础设施)来参与保证
密码学最基础的分支有三个:
1. 第一个是单向散列函数
2. 第二个是对称密码技术
3. 第三个是非对称密码技术
02 | 单向散列函数: 如何保证信息完整性¶
一个实用的单向函数,计算强度和破解强度要均衡考量,不可偏废。
单向函数(One-way Function)是正向计算容易,逆向运算困难的函数。
散列函数(Hash Function)是一个可以把任意大小的数据,转行成固定长度的数据的函数。
单向散列函数既是一个单向函数,也是一个散列函数:
逆向运算困难 构造碰撞困难
散列值碰撞: 存在散列值相同的两个或者多个数据
散列值越长,存在相同散列值的概率就越小,发生碰撞的可能性就越小。散列值越长,通常也就意味着计算越困难,计算性能越差。散列值的长度选择,应该是权衡性能后的结果。
降低散列值碰撞的可能性:
1. 增加散列值长度
2. 使用一个好的散列函数,它的散列值应该是均匀分布的
备注
雪崩效应(Avalanche Effect)是密码学算法一个常见的特点,指的是输入数据的微小变换,就会导致输出数据的巨大变化。严格雪崩效应是雪崩效应的一个形式化指标,我们也常用来衡量均匀分布。严格雪崩效应指的是,如果输入数据的一位反转,输出数据的每一位都有 50% 的概率会发生变化。
03 | 如何设置合适的安全强度¶
最常用的指标就是安全强度(Security Strength)
安全强度¶
在密码学中,安全强度通常使用“位”(字节位)来表述。比如说,安全强度是 32 位。这里的“位”是什么意思?N 位的安全强度表示破解一个算法需要 2^N(2 的 N 次方) 次的运算。
MD5 的安全强度是不大于 18 位
1024 位的 RSA 密钥的安全强度是 80 位
SHA-256 算法的安全强度是 128 位
备注
组合的强度,由最弱的算法和密钥决定
破解速度¶
破解速度:对安全强度最多 18 位的MD5,运算 2^18=262144 次就可以破解,按普通的计算机一毫秒一次运算的速度计算,需要 262144 毫秒,折合 4.34 分钟。假设我们现在有一台速度快 1000 倍的计算机,它能做到 1 纳秒运算一次,同时使用 10 亿台计算机。破解 128 位的安全强度的需要一千万个十亿年;破解80 位的安全强度,同样的条件,破解大概需要 38 年。
破解速度:使用最快计算机(Fugaku)的数据来说是415530TFlops, 大约是每秒4.2*10^17次浮点运算,破解64位强度的话大约需要44s。80位的话大约需要2878395s也就是34天左右,如果是128位的话大约需要25691150168585年
备注
一个算法的安全强度不是一成不变的。随着安全分析的进步,几乎所有密码学算法的安全强度都会衰减。今天看起来安全的算法,明天也许就有破解的办法。所以,一个好的安全协议,应该考虑备份计划和应急计划
单向散列函数 SHA-1 在 1993 年发布的时候,它的设计安全强度是 80 位。 12 年后,在 2005 年 2 月,中国密码学家王小云教授带领的研究团队发现,SHA-1 的安全强度小于 69 位,远远小于设计的 80 位。从此,SHA-1 的安全强度开始一路衰减。很快,2005 年 8 月,王小云教授的团队又改进了破解算法,发现 SHA-1 的安全强度只有 63 位了。2015 年 10 月,密码学家马克·史蒂文斯(Marc Stevens),皮埃尔·卡普曼(Pierre Karpman)和托马斯·佩林(Thomas Peyrin)的研究团队发现 SHA-1 的安全强度只有 57.5 位。
破解费用:你可以感受下密码强度和破解成本的数字-> 如果使用云计算,按照 2015 年亚马逊 EC2 云计算的定价和算力,57 位的安全强度,2015 年的破解成本大致是 10 万美元。2020 年 1 月,密码学家盖坦·勒伦(GaëtanLeurent)和托马斯·佩林(Thomas Peyrin)又发现, SHA-1 的攻击复杂度是 63.4 位,攻击成本大约为 4.5 万美元。根据上面的数字,我们可以感受到,一个 64 位安全强度的密码算法,它现在的破解成本大概是 5 万美元左右。
备注
安全强度和攻击复杂度是同一个指标的两种不同的说法,一个从正面说,一个从反面说。
常用指标¶
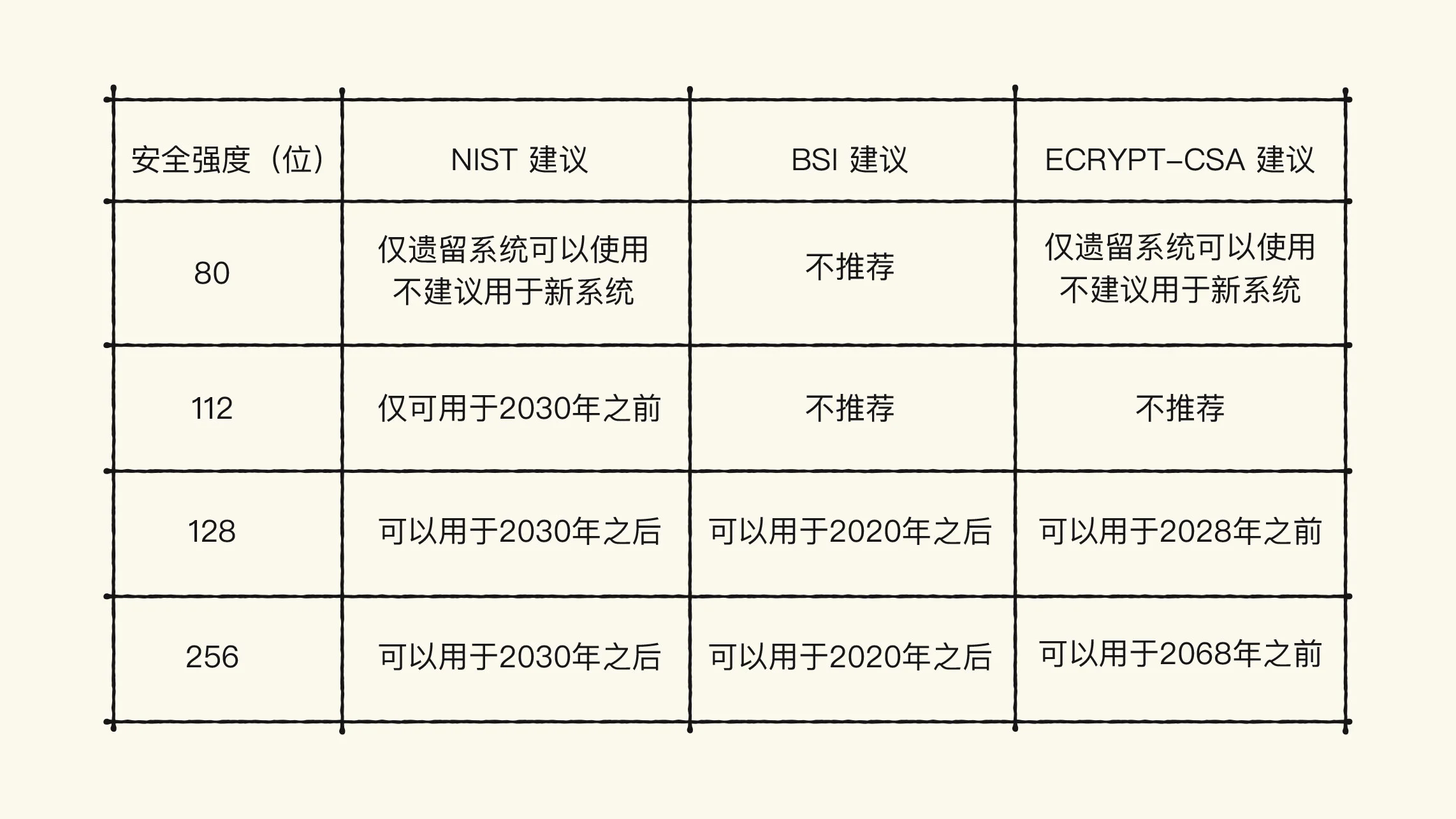
业界内最新推荐的三个常用指标分别是:
1. 美国的 NIST(国家标准技术研究所)
2. 德国的 BSI(联邦信息安全办公室)
3. 欧洲的 ECRYPT-CSA(欧洲卓越密码网络)
caption¶
04 | 选择哈希算法应该考虑哪些因素¶
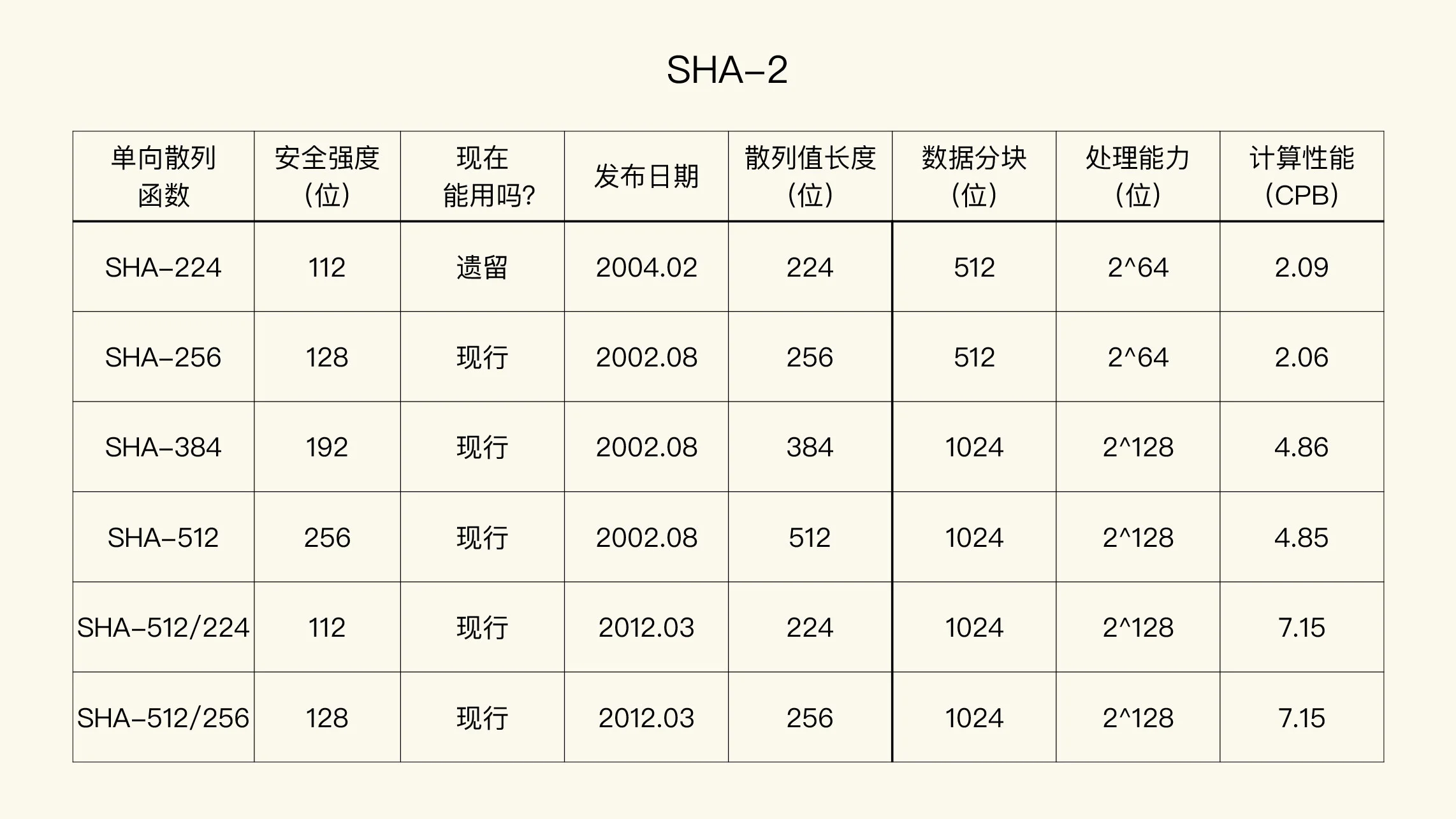
对于单向散列函数,现行的、流行的算法:
1. SHA-256
2. SHA-384
3. SHA-512
可用的算法¶
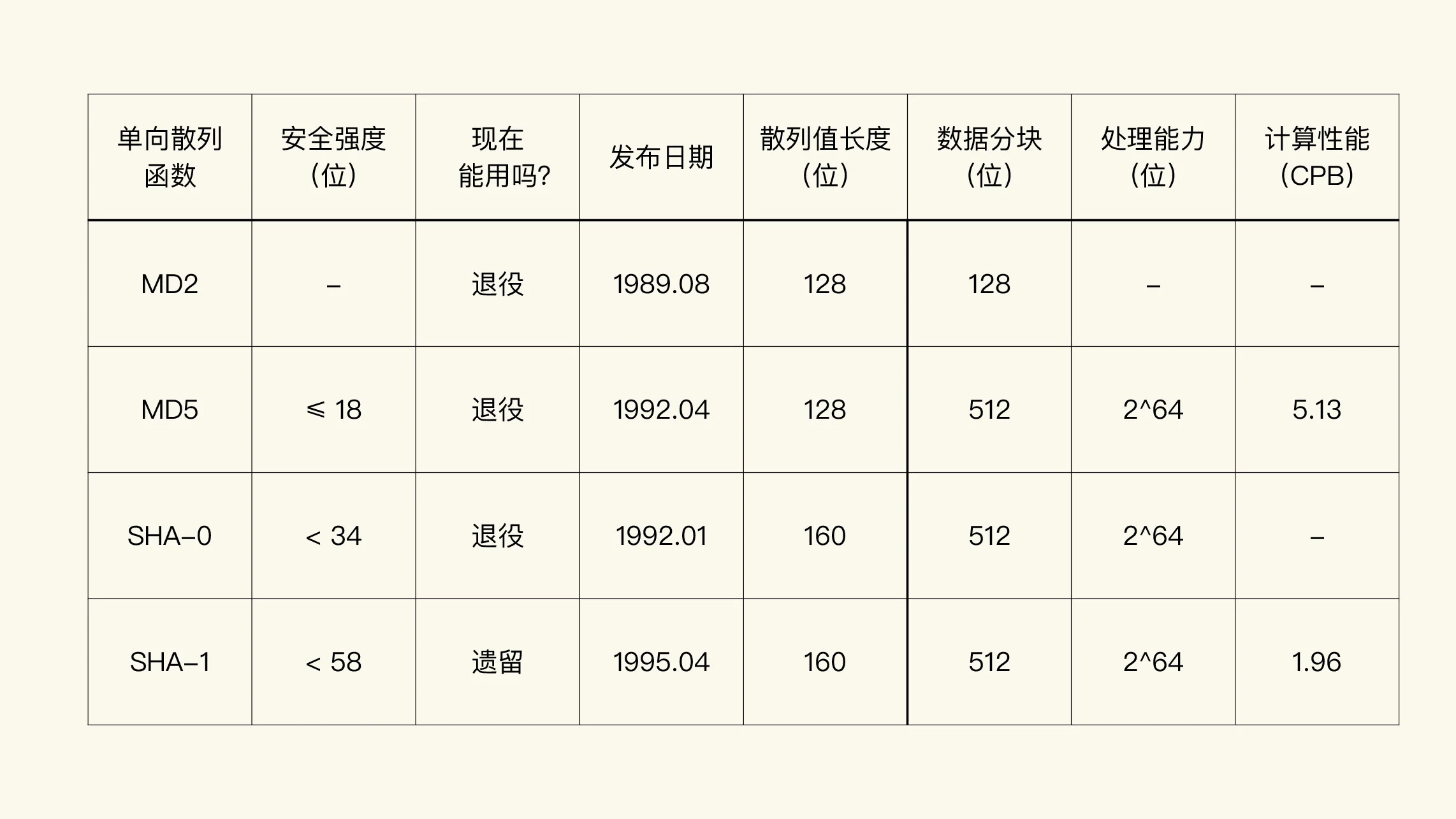
判断一个现存的算法,还能不能继续使用是我们选择算法的第一步。根据这个标准,把常见的算法分为了以下三类:
1. 退役的算法
2. 遗留的算法
3. 现行的算法
处理能力限制¶
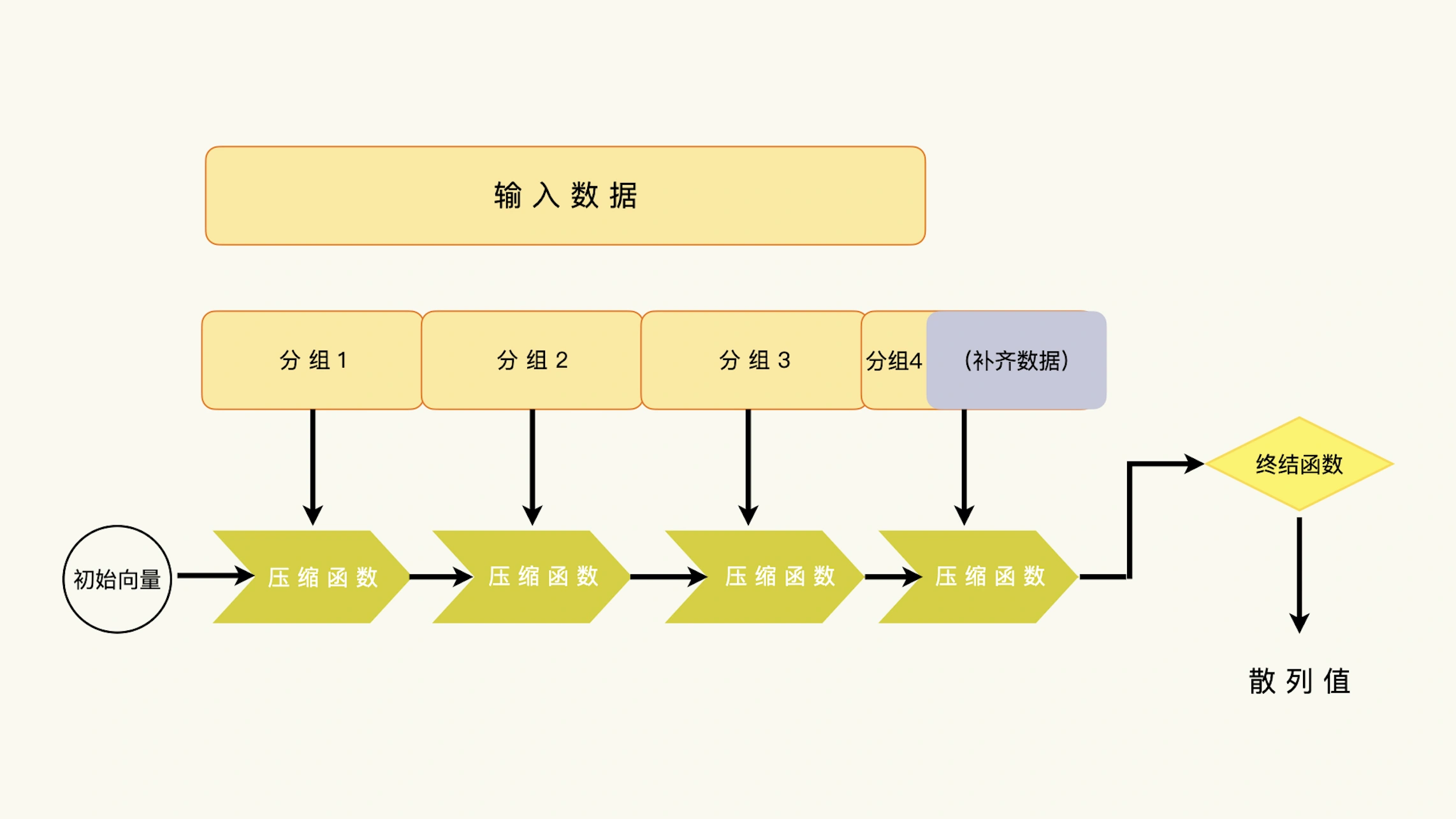
一个典型的单向散列函数,由四个部分组成:数据分组、链接模式、单向压缩函数和终结函数。一般来说,压缩函数能够接收的数据块大小是固定的。比如 SHA-256 的压缩函数只能处理 512 位的数据,多一位不行,少一位也不行。¶
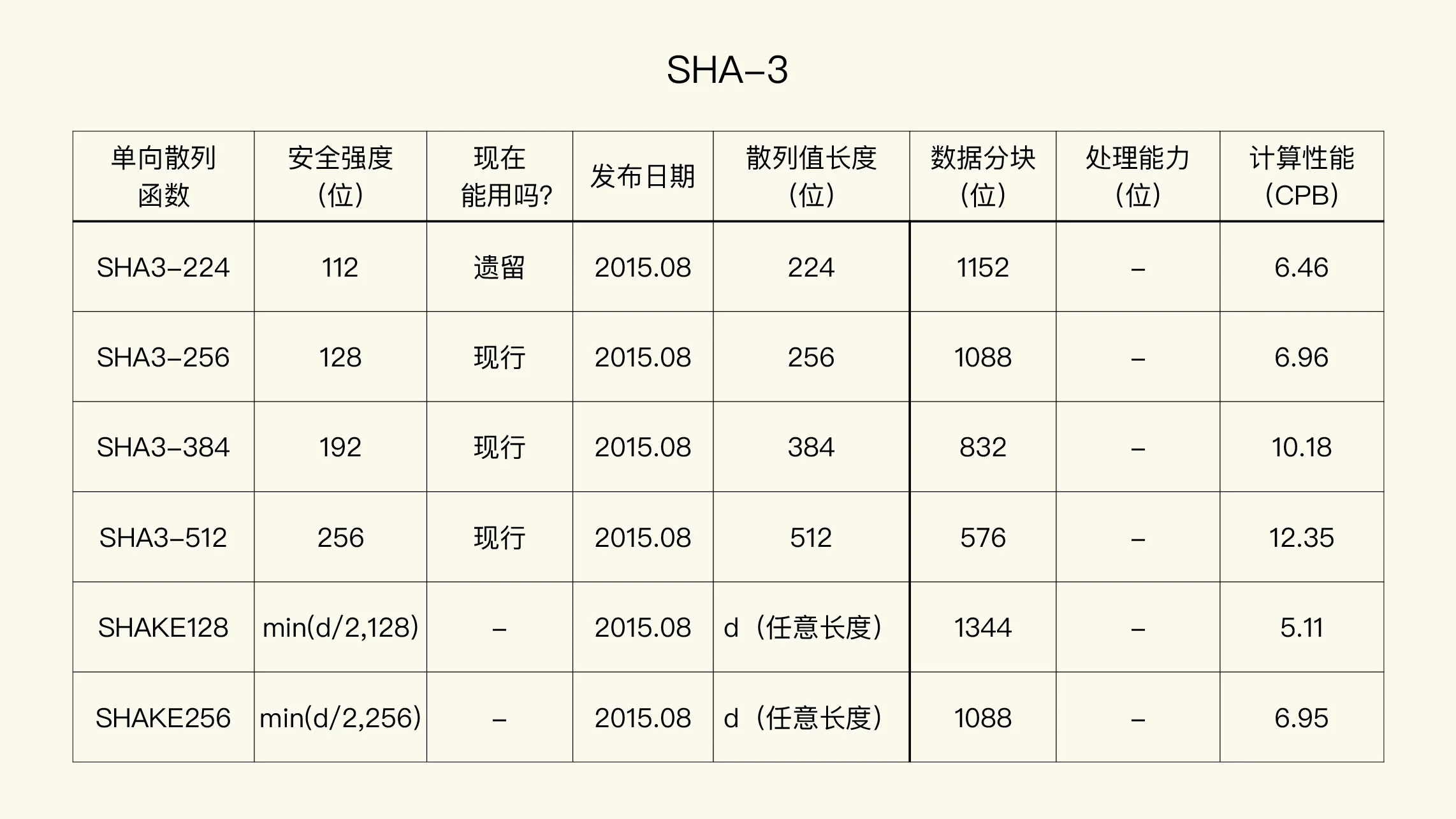
如果输入数据长度超过了数据补齐方案的限制,数据就没有办法分组了。这就是单向散列函数数据处理能力限制的来源。SHA-3 的设计,放弃了在数据补齐方案里使用固定位数表示输入数据长度的做法,它也就不再有数据处理能力的限制。
参考-单向哈希函数关于输入数据能力的限制: https://blog.csdn.net/u011583927/article/details/80905740/
05|如何有效避免长度延展攻击¶
备注
【定义】单向散列函数的长度延展:假设我们有两段数据,S 和 M,以及一个单向散列函数 h。如果我们要把这两段数据合并起来,并且还要计算合并后的散列值,这就叫做单向散列函数的长度延展。
备注
S 放在前面(h (S|M)),还是 M 放在前面(h (M|S))。如果 S 和 M 都是公开的信息,顺序是不重要的。可如果 S 是机密信息,M 是公开信息,这两段数据的排列顺序就至关重要了。如果机密信息放在了前面,就存在 “长度延展攻击” 的风险。
备注
【定义】长度延展攻击:可以利用已知数据的散列值,计算原数据外加一段延展数据后的散列值。也就是说,如果我们知道了 h (S|M),我们就可以计算 h (S|M|N)。其中,数据 N 就是原数据追加的延展数据。
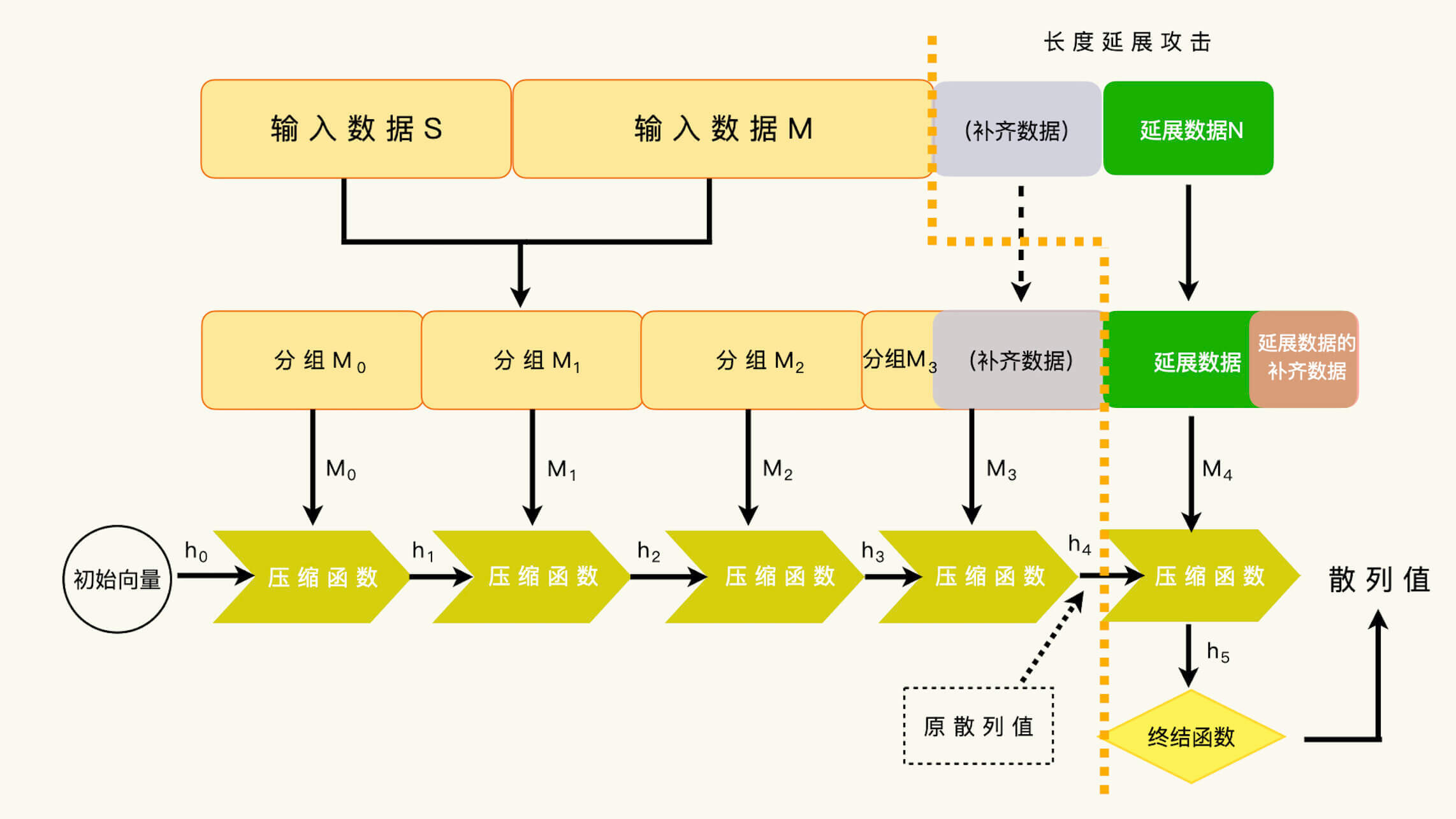
单向散列函数长度延展攻击示意图¶
对于下列算法,长度延展攻击是完全有效的:
MD2
MD5
SHA-0
SHA-1
SHA-256
SHA-512
对于下列算法,长度延展攻击虽然不是完全有效,但是算法的安全级别显著降低了:
SHA-224
SHA-384
对于下列算法,长度延展攻击没有效果(包括所有的 SHA-3 算法):
SHA-512/224
SHA-512/256
SHA-3
不要单纯使用单向散列函数来处理既包含机密信息、又包含公开信息的数据。即使我们把机密信息放在最后处理,这种使用方式也不省心。
备注
如果我们需要使用机密数据产生数据的签名,我们应该使用设计好的、经过验证的算法,比如我们后面会讨论的消息验证码(Message Authentication Code)和基于单向散列函数的消息验证码(Hash-based Message Authentication Code)。
单向散列函数的场景:
1. 校验数据完整性
2. 数字签名,和非对称密钥及其算法结合使用
3. 消息验证码,和对称密钥及其算法结合使用
4. 生成伪随机数
5. 生成对称密钥
06|对称密钥: 如何保护私密数据¶
密文(Ciphertext)
明文(Plaintext)
口令(Password)
密钥(Key)
加解密算法(Cipher)
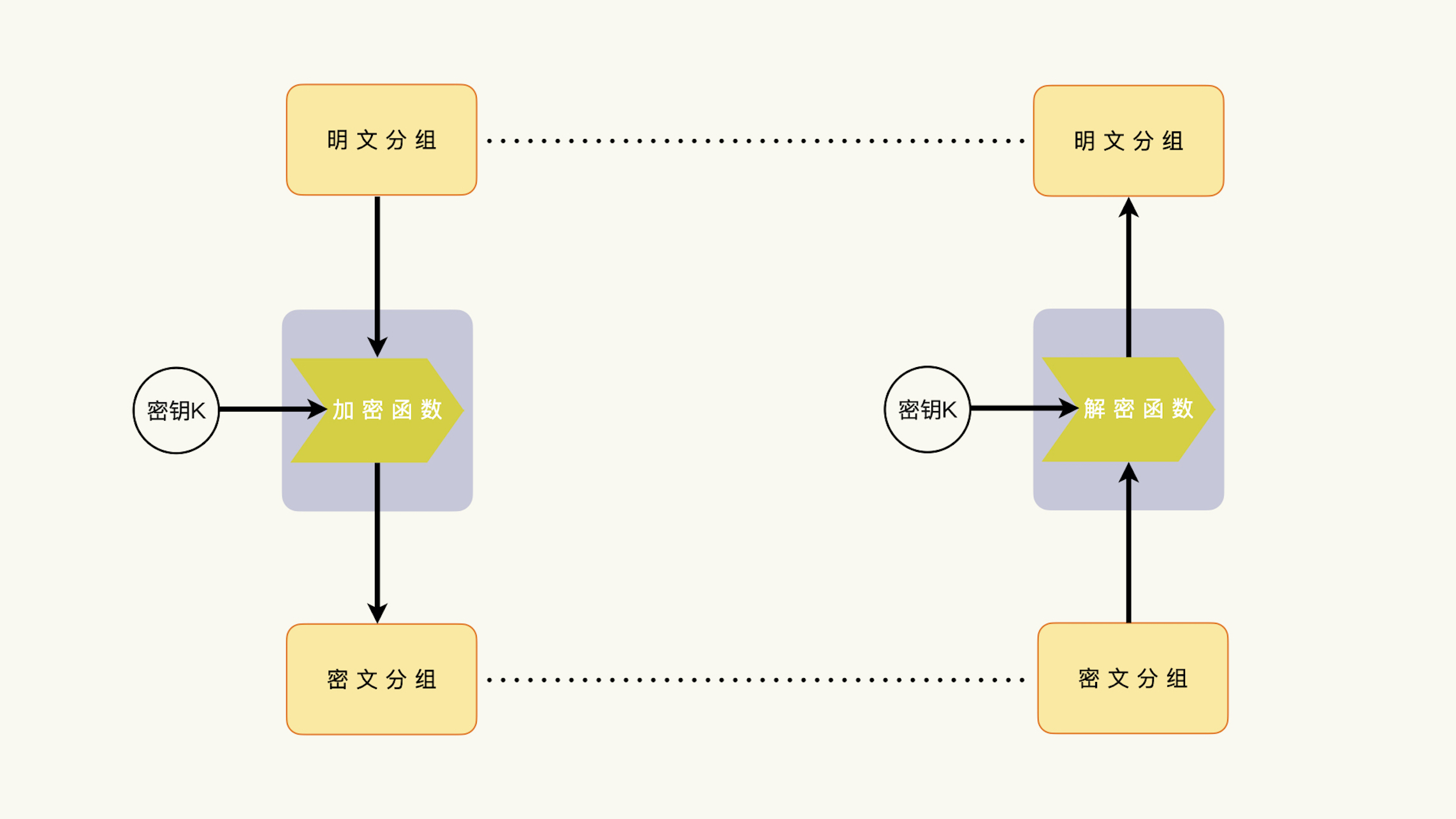
什么是加密¶
历史上的加密,是没有密钥的。数据的保密性,依赖于算法的保密性。到了现代密码学,加密数据的安全性就依赖于加密算法的质量和密钥的保密性这两个因素。密钥部分,是私有的部分,需要严格保密;算法部分,变成了公开的部分,要接受公开讨论、评测,接受各种分析和攻击。
一个算法,如果在接受了公开的分析、评测和各种各样的攻击之后,还依然被认为是安全的,我们才能说,这个算法的安全性是真的经得起考验的。¶
备注
在遴选标准中,有一个重要指标,就是有没有足够多的密码分析。密码分析,指的是分析、评测一个密码学算法,有没有安全缺陷和适用场景的限制。如果一个算法,没有人对它展开分析、评测,或者缺少足够的分析,它的安全性很难获得信任。
使用公开的算法是密码学领域的一个基本常识。不过,一个现代密码学算法的安全性,都是基于密钥的保密,而不是算法保密要求。仍然有很多保密算法的存在和使用。对于这样的使用,我们很难有信心相信它的安全性。
两个密码学常识:
1. 不要自己发明密码算法,尤其是在没有经过充分讨论、充分分析的情况下。
大部分情况下,我们自行发明的密码学算法都是灾难。
2. 不要把安全性寄托在算法的保密上。
大部分情况下,保密的算法都是无法保密,并且是不堪分析的。
备注
现代的密码学算法的安全性,都是基于密钥的保密,而不是算法保密要求。管理好密钥,做好密钥的保密,才是密码学系统最关键的任务。
什么是对称密钥¶
1976 年,惠特菲尔德・迪菲(Whitfield Diffie)、马丁・赫尔曼(Martin Hellman)发表了基于非对称密钥技术的密钥交换算法,但是在这之前,并没有对称密钥、非对称密钥的说法。即:1976 年之前,密码学就是一门研究对称密钥的学问。
07 | 怎么选择对称密钥算法¶
数据加密影响性能吗¶
对称加密的加密、解密运算是一种很快的运算。每个字节的加密、解密运算需要大约 0.5 个时钟周期。
和 HTTP 协议相比,在 HTTPS 协议通道上传输的应用数据,都是加密的数据。有测试数据表明,和 HTTP 相比,一个合理配置的 HTTPS 服务,客户端的响应时间没有明显的变化;服务器的吞吐量大约减少了 5% 到 8%,CPU 的使用大约增加了 2% 到 5%。
序列算法和分组算法¶
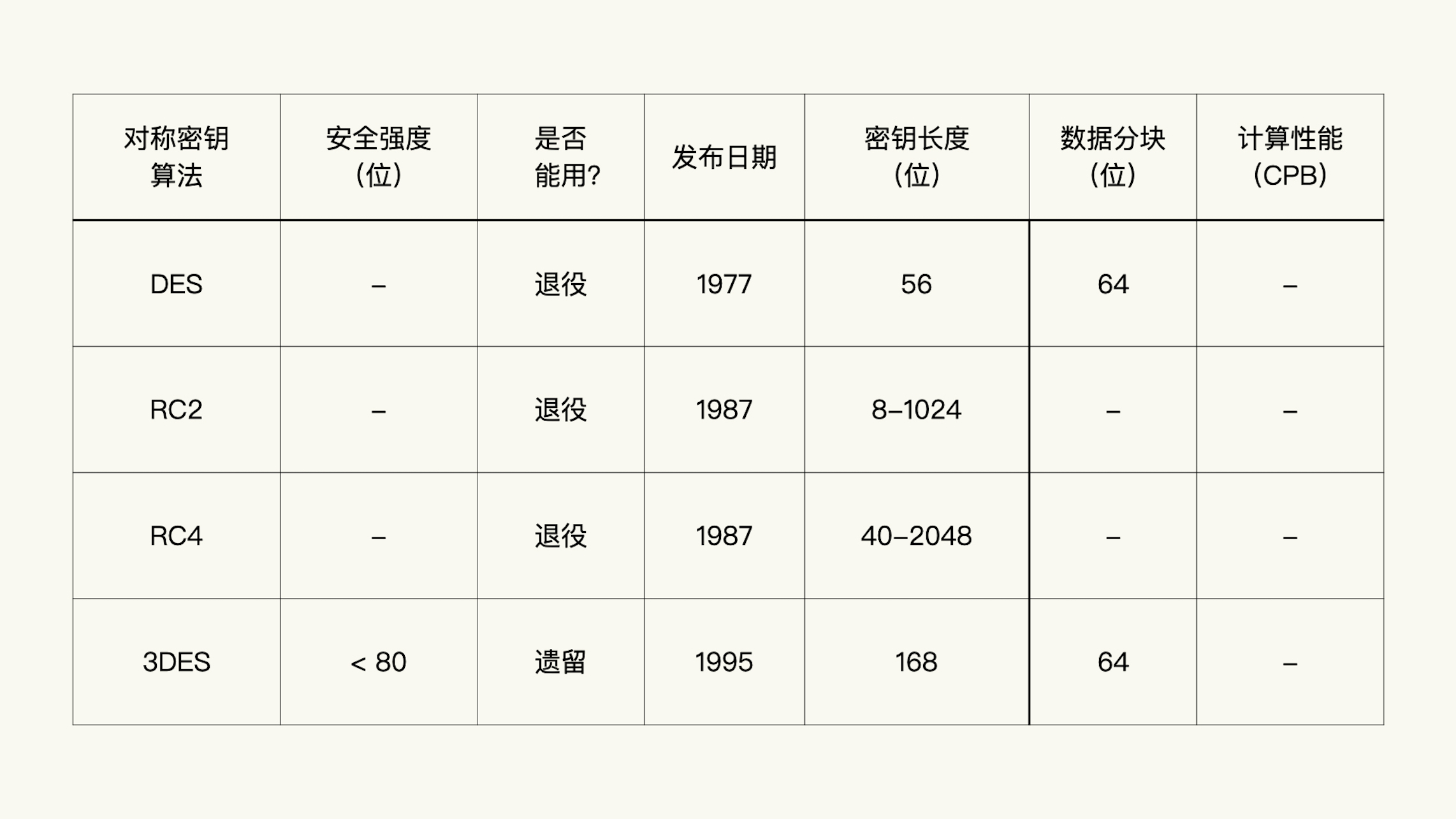
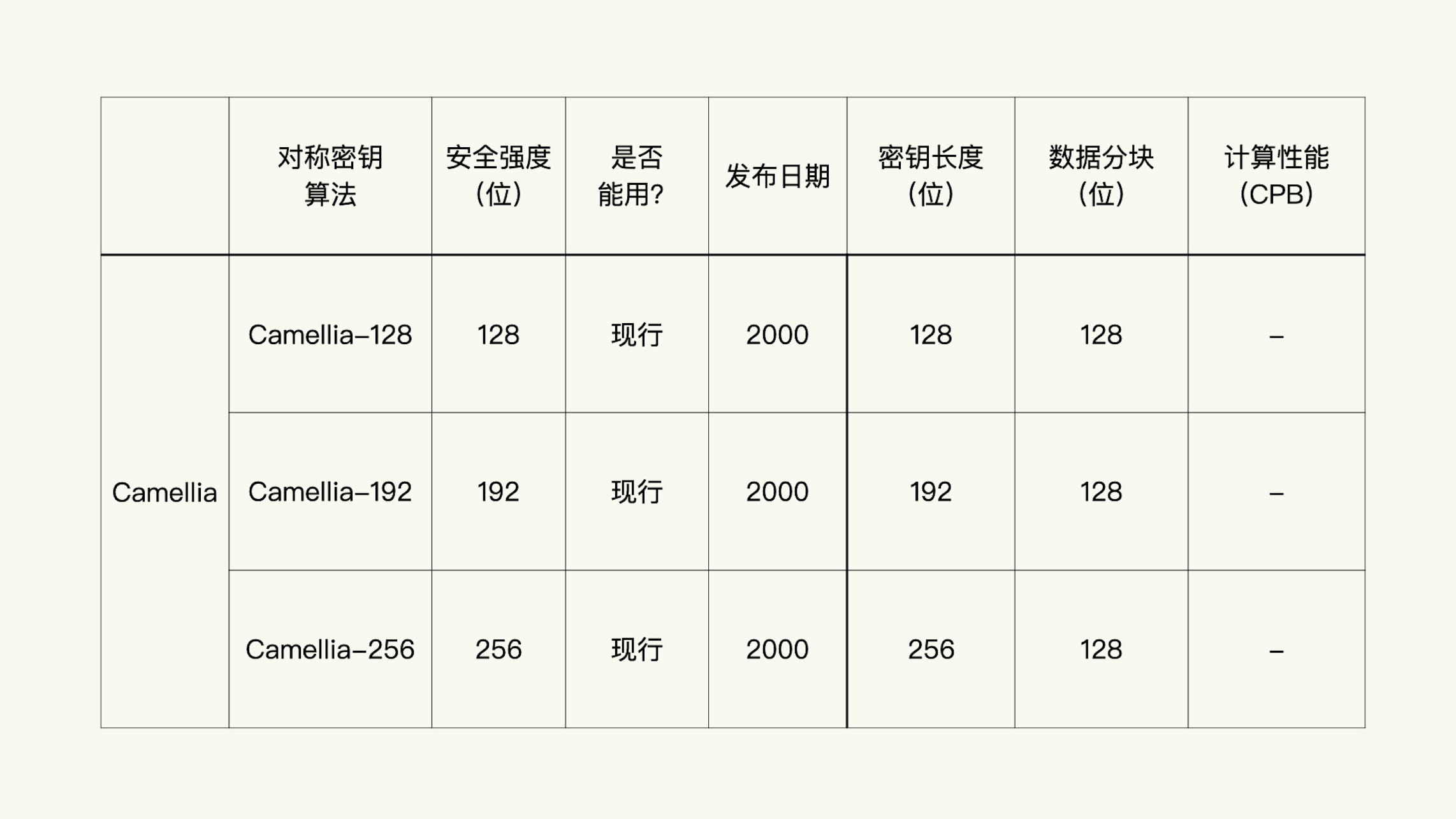
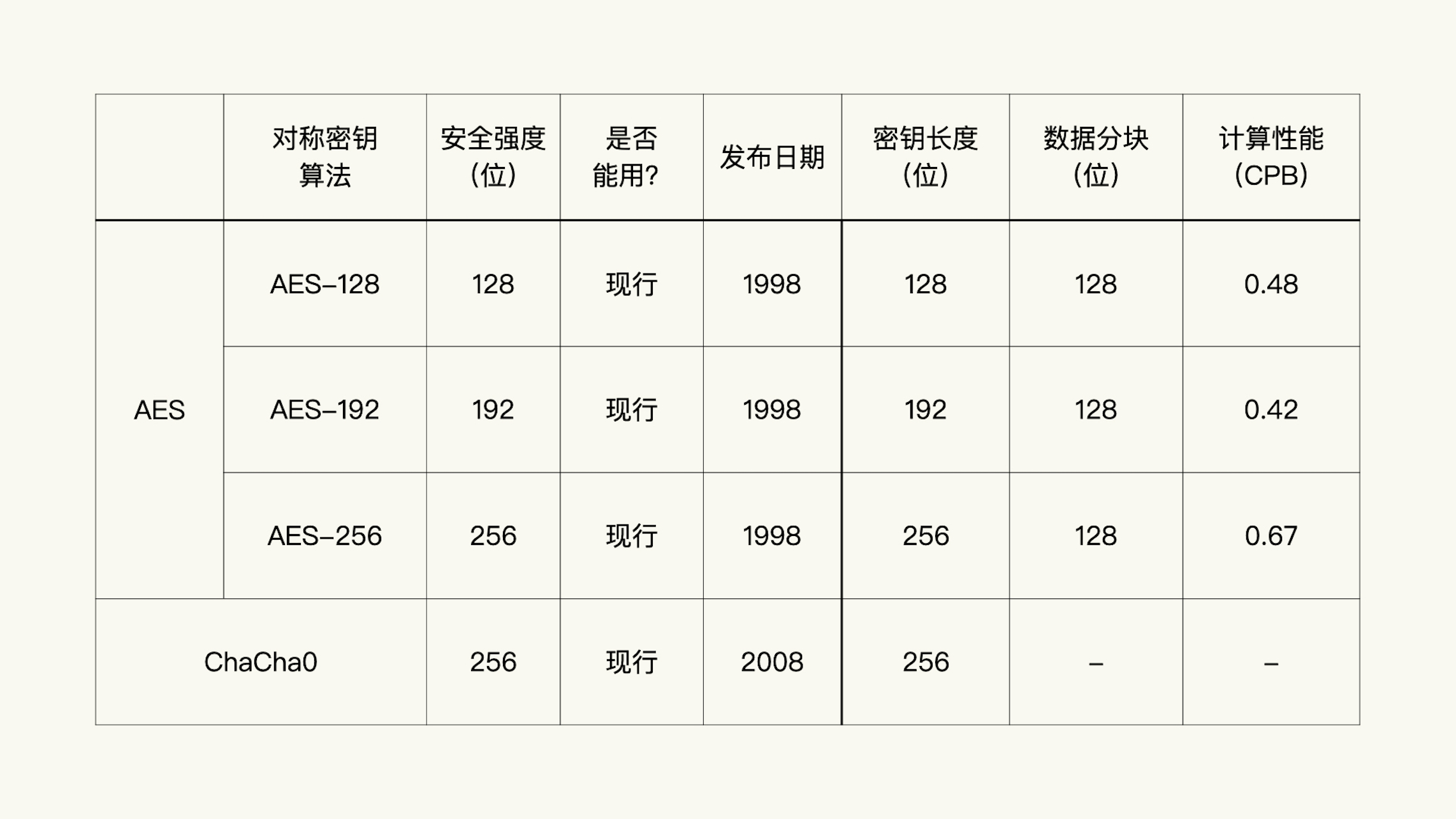
在上面的表格里,RC4 和 ChaCha20 没有数据分块数据,而 3DES 和 AES 有数据分块数据。这是因为 RC4 和 ChaCha20 是序列算法,3DES 和 AES 是分组算法。
从数据是否分组这个角度考虑,就有两种处理方式:
1. 进行数据分组,然后按数据组运算,这就是分组算法
2. 不进行数据分组,按照原始数据的大小进行运算,这就是序列算法
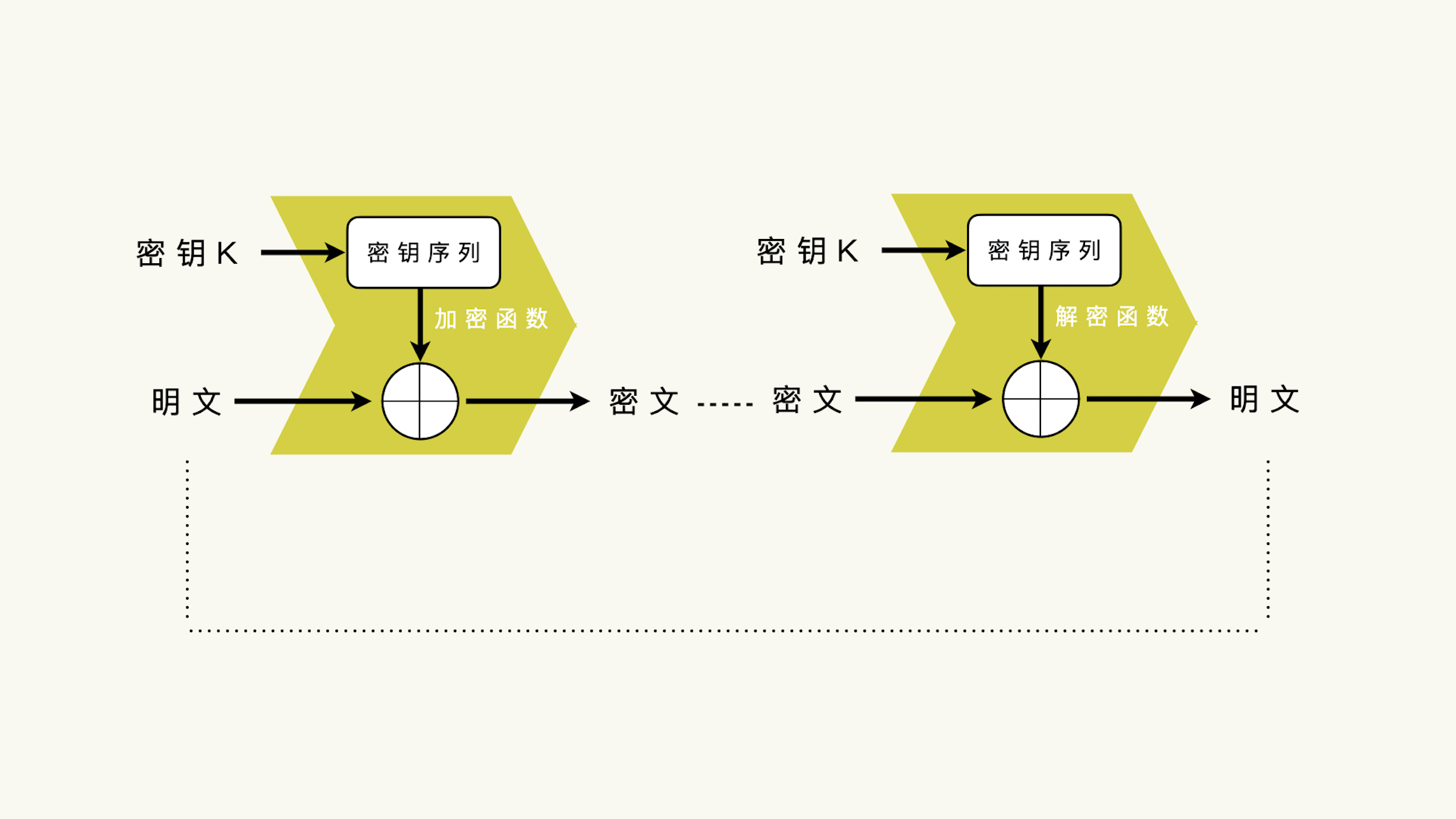
序列算法的基本思路,就是从对称密钥里推导出一段和明文数据相同长度的密钥序列,然后密钥序列和明文进行亦或运算得到密文,和密文进行异或运算得到明文。¶
备注
在类似的条件下,相同安全强度的对称密钥,ChaCha20 算法要比 AES 算法快四到六倍,比 Camellia 算法快近十倍。ChaCha20 是现代主流浏览器优先选择的加密算法。
参考文献¶
DES:RFC 18229
RC2:RFC 2268
3DES:RFC 1851
Camellia-128、192、256:RFC 3713
AES-128、192、256:FIPS 197
ChaCha20:ChaCha
08 | 该怎么选择初始化向量¶
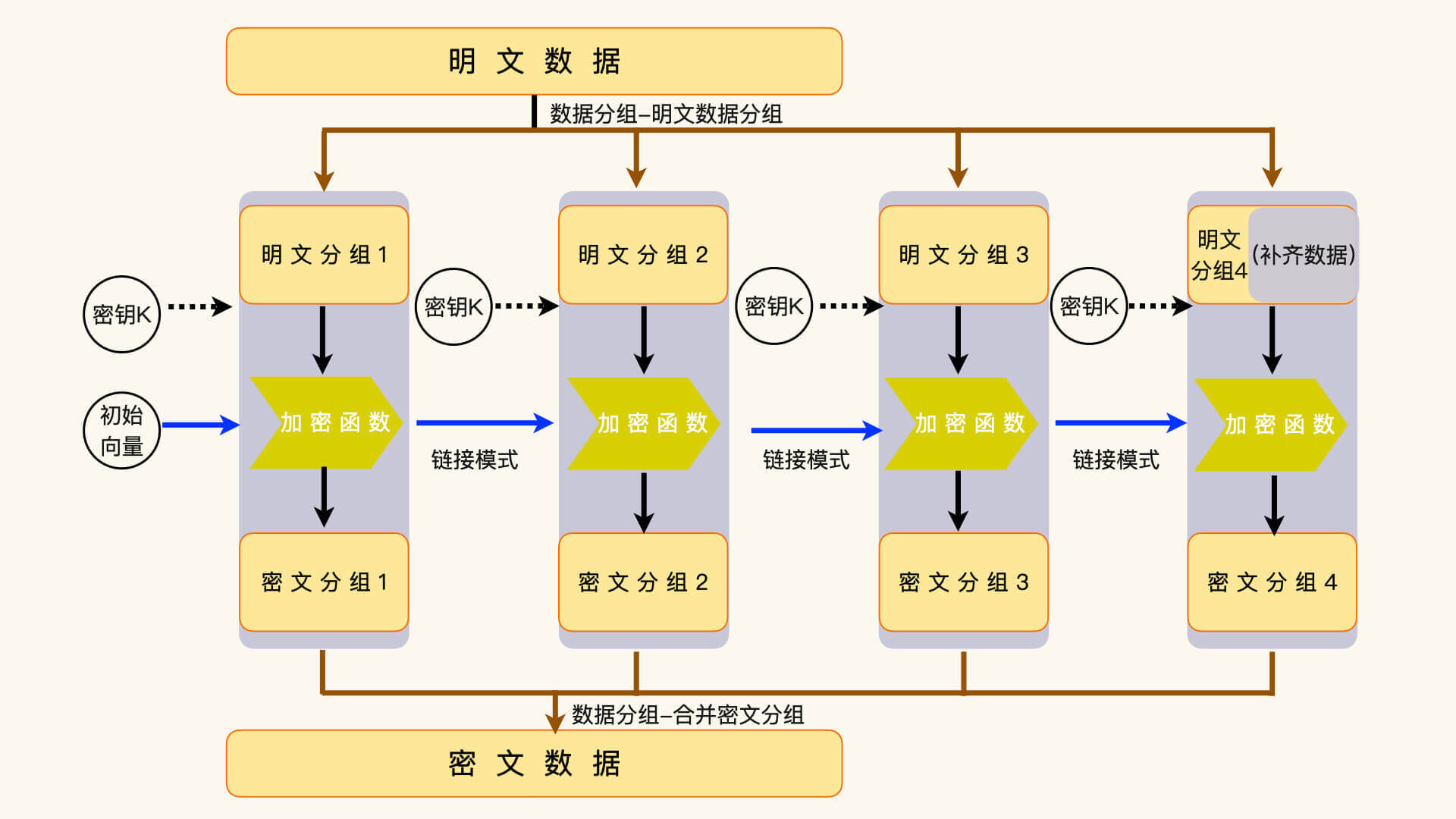
分组算法要对输入数据进行分组,然后按数据分组来进行运算。一个典型的分组算法,一般要由三个部分组成,数据分组、分组运算和链接模式。数据分组在加密时,会把明文的输入数据分割成加密函数能够处理的数据块。比如,AES 算法能够处理的数据块大小是 128 位,那么,输入数据就要被分割成一个或者多个 128 位的小数据块。如果不能整分,就要把最后一个分组补齐成 128 位。这些分组数据的运算结果,组合起来就是密文数据。¶
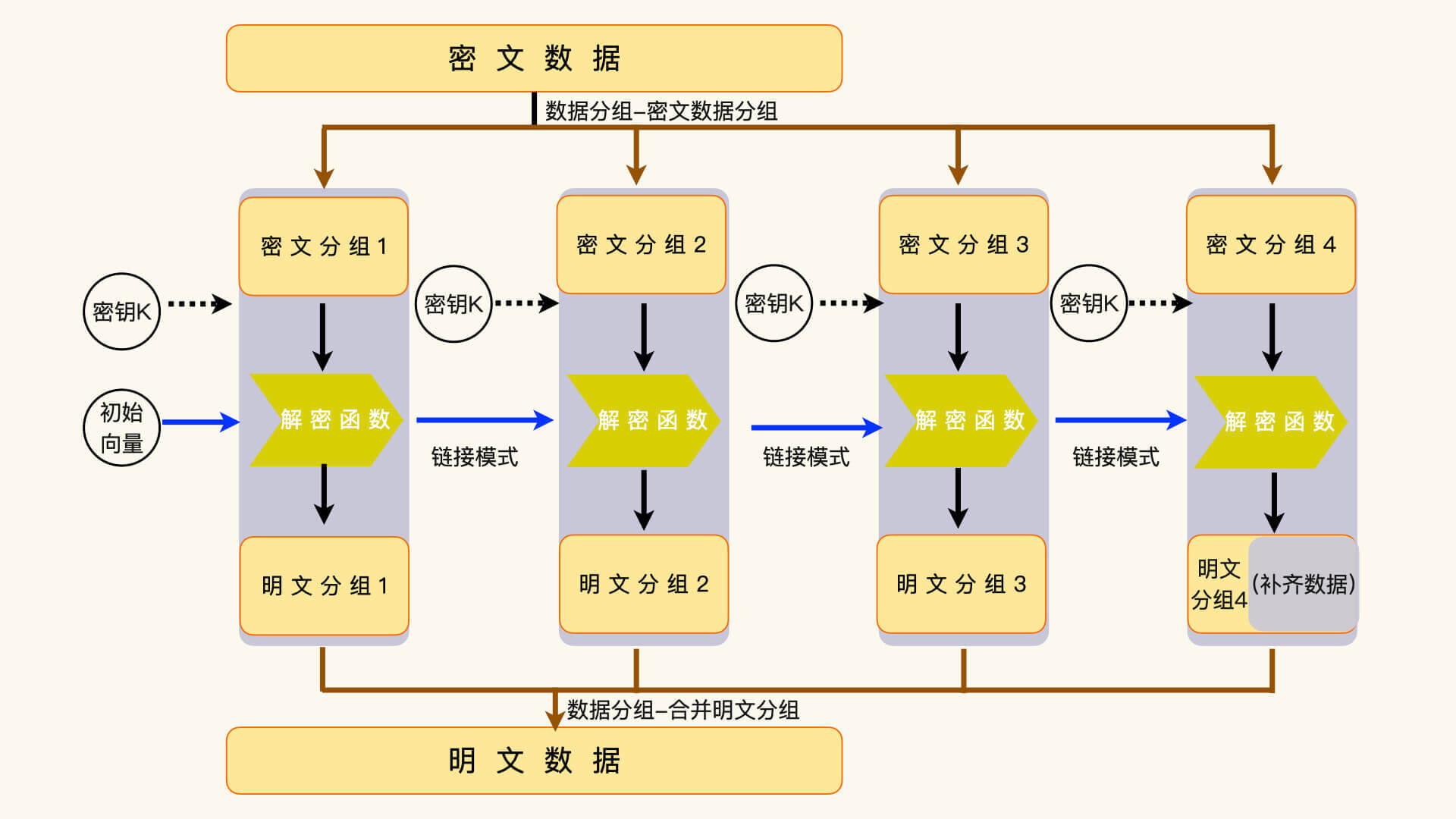
解密时,执行相反的操作,把补齐数据去掉,再把数据分组组合成完整的明文数据。¶
链接模式,指的是如何把上一个分组运算和下一个分组运算联系起来。第一个分组运算并没有上一个分组运算可以使用,这时候,我们就需要引入一个初始化的数据,来承担“上一个分组运算”向下链接的功能。这个初始化的数据,我们一般称为初始化向量。
在分组运算里,链接模式承担着类似确保雪崩效应能够延续的作用:
1. 不同的明文数据,它的密文数据应该是完全不同的,即使明文数据里包含相同的数据分组
2. 相同的明文数据,每一次的加密运算,它的密文数据也应该是完全不同的
什么影响算法的安全性¶
五个因素:
1. 加密函数和解密函数
2. 密钥
3. 初始化向量
4. 链接模式
5. 数据补齐方案
初始化向量怎么选¶
第一个数据块和初始化向量关系紧密。第一个数据块的计算,它的输入信息包括:
1. 密钥
2. 初始化向量
3. 第一个明文数据分组
备注
第一个明文数据分组(对AES来说16字节)相同的情况还是挺多的,使用同一对称密钥加密时,如果初始化向量一样,第一个密文数据分组肯定是相同的。在现实的应用里,也存在大量的、重复的、已知的数据,比如 HTTP 协议的头部数据。如果我们需要保密的数据恰好重复了一段已知的明文,攻击者就可以根据密文数据是不是相同,来猜测、寻找明文数据。这样的话,就破坏了数据的保密性。
重要
在一个对称密钥的生命周期里,初始化向量不能重复,这是使用对称密钥算法的第一个要求。
初始化向量的选择:
1. 使用安全强度足够的随机数作为初始化向量;
随机数的获取,有时候不是一个有效率的运算
如何在加密端和解密端同步初始化向量,也是一个需要考虑的问题
常见的解决办法,就是把初始化向量和加密数据一起发送给对方
2. 使用序列数,下一次的初始化向量的数值,比上一次的数字自动加一或者自动减一。
序列数状态的保持和同步问题
除了效率之外,还会衍生出其他的待解决的问题,
比如分布式计算环境下的序列数同步问题,
比如攻击者会知道每一个初始化向量的问题。
初始化向量选择充满了复杂性,一般的密钥算法库都不会提供缺省的、自动的初始化向量。应用程序需要根据使用场景来制定适当的初始化向量选择方案,这是一个容易忽略的要求。
一个密钥能用多少次¶
在一个对称密钥的生命周期里,初始化向量不能重复。如:一个 128 位的初始化向量,最多有 2^ 128 个不重复的数值。还有其他因素限制密钥的使用次数。很多限制因素的叠加,就会使得密钥使用的限制数远远低于初始化向量的许可数目
09 | 为什么ECB模式不安全¶
ECB 模式什么样¶
ECB 模式有所不同,它不使用链接模式,因此它也用不着初始化向量。不使用链接模式,就意味着上一个分组运算不影响下一个分组运算,每一个数据分组的运算都是独立的。¶
备注
初始化向量的缺失和链接模式的缺失会带来致命的安全陷阱。
缺失带来了什么问题¶
实例:
明文: ABCDEFGHHIJKLMNO0123456789012345
使用 AES-128/ECB 算法加密时,分成两个明文分组:
ABCDEFGHHIJKLMNO
0123456789012345
加密这段数据,得到的密文(密钥“1234567890123456”)
1389AE9853633EBF3D35F28987FCD1187B4BFC89DD1700154482BC7EB686BB0E
把密文按照块大小分成两段
1389AE9853633EBF3D35F28987FCD118
7B4BFC89DD1700154482BC7EB686BB0E
那么:
密文:7B4BFC89DD1700154482BC7EB686BB0E1389AE9853633EBF3D35F28987FCD118
对应的明文是:
明文:0123456789012345ABCDEFGHHIJKLMNO
备注
通过上面的实例就可以进行“分组重放”攻击,在加密未破解的情况下实现攻击。
10 | 怎么防止数据重放攻击CBC¶
CBC 模式,可能是 2018 年之前最常用、最常见的加密模式。和 ECB 模式不同,由于初始化向量和链接模式的使用,CBC 模式解决了数据重放攻击的问题。可是,从 2018 年开始,由于它的安全问题,CBC 模式开始退出历史舞台,尽管这一进程可能需要十数年,甚至数十年。最有标志性的事件就是TLS 1.3协议彻底放弃的CBC算法。
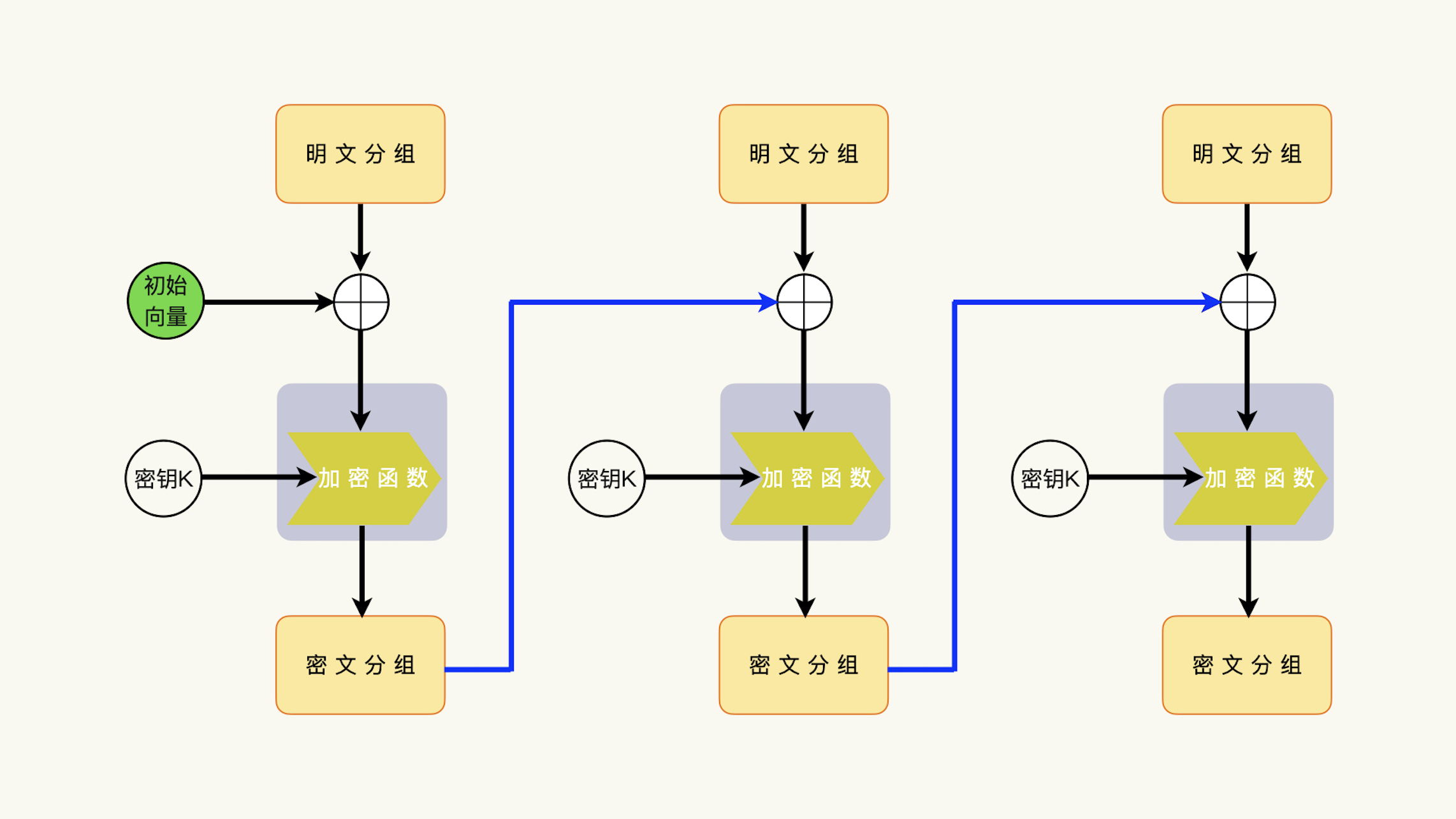
在加密过程中,加密函数的输入数据是明文分组(Mi)和上一次的密文分组(Ci-1)的异或运算的结果(Mi ^ Ci-1)。¶
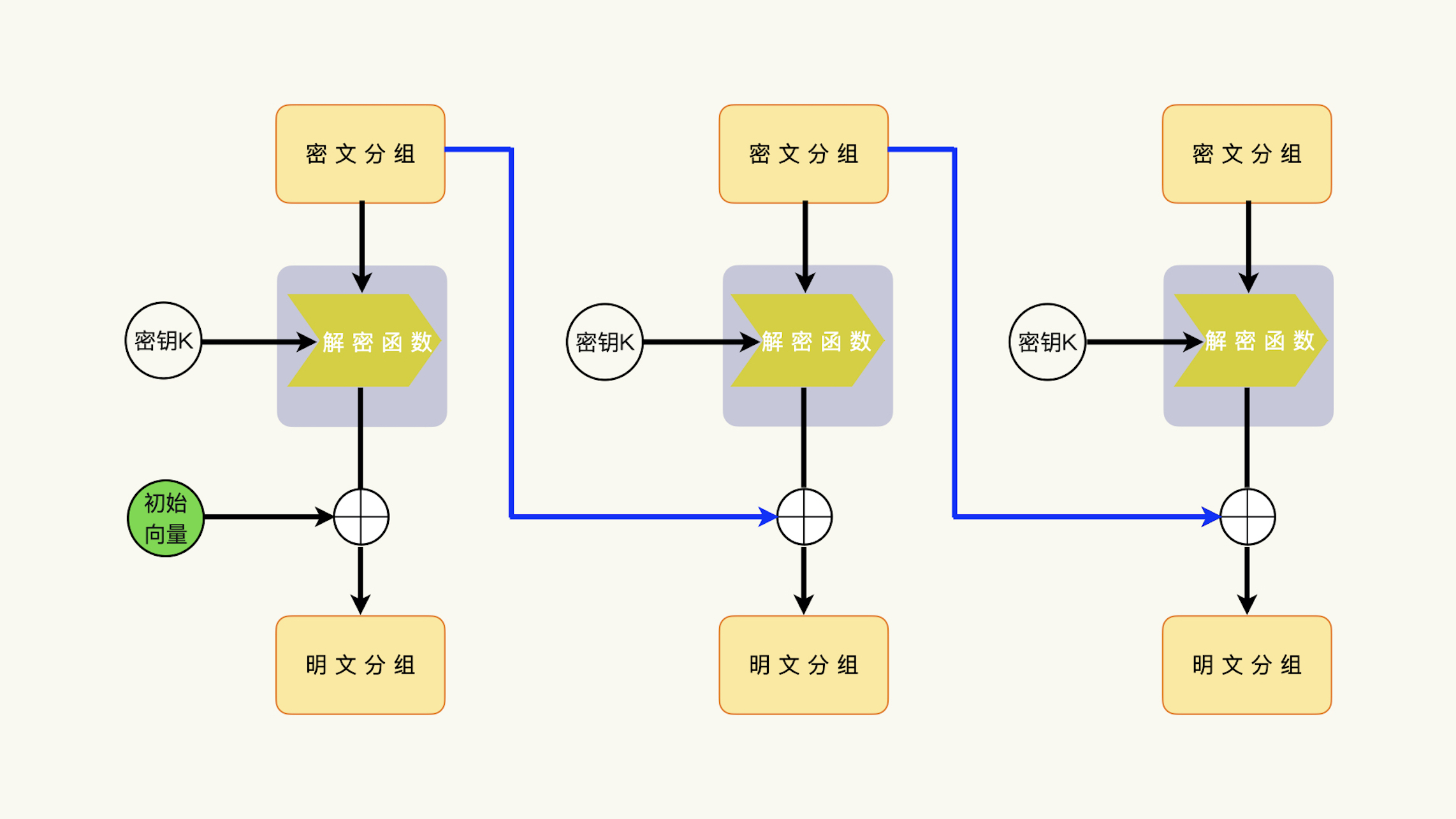
在解密过程中,解密函数的输出数据,也是明文分组和上一次的密文分组的异或运算结果(Mi ^ Ci-1)。初始化向量只影响第一个明文分组,并不影响后续的解密过程和明文分组;一个密文分组,只影响它的下一个明文分组,并不影响更后面的解密过程和明文分组。而在加密过程中,每一个密文分组,都依赖于前面所有的明文分组,包括初始化向量。¶
理解 CBC 模式的三个关键点:
1. 加密和解密要使用初始化向量
2. 加密和解密的初始化向量是等同的
3. 上一次的密文分组参与下一次的加密和解密运算
初始化向量需要保密吗¶
如果每一次运算,初始化向量都能不重复,即使是相同的明文数据,它的加密结果也是不同的。但是,如果初始化向量重复使用,相同的明文就会有相同的密文。重复使用的初始化向量,会消解密文反馈的作用,使得 CBC 模式和 ECB 模式一样脆弱。
备注
初始化向量的唯一性在加密运算的安全性中至关重要。但初始化向量并不需要保密。
异或运算会不会有问题¶
异或运算应用广泛的三个原因:
1. 异或运算是按位运算,在相同环境下,运算时间只和数据位数相关,和实际数值无关
放在密码学算法的世界里,如果运算时间和实际数值无关,那简直再好不过了。
换句话说,如果运算时间和数据数值相关,而且别人还了解到这种相关性,
他就可以通过统计学的方法,通过观察、测算运算时间,
找到运算时间和数据数值之间的关联,来破解密码。
2. 也是按位运算,在相同环境下,运算的复杂度(算力)只和位数相关,和实际数值无关
一个运算需要的算力,可以通过占用的 CPU 周期数,以及消耗的内存空间来衡量。
同理,如果占用的 CPU 或者消耗的内存和数据数值相关,
就可以通过统计学的办法,观察 CPU 的占用、电力消耗或者内存的消耗,来破解密码。
一般来说,这种相关性也会影响运算时间,使得基于测算运算时间的攻击方式同样有效
不光如此,如果运算的复杂度和数据数值相关,密码破解的办法可就是千奇百怪的了。
记录、测算计算机的噪音、温度、辐射、反应时间等等,都有可能成为有效的攻击手段。
如让一流的黑客,拿手机进入数据中心,录一段服务器的声音,可能服务器就会被攻陷。
没有说一定被攻破,是因为近几年密码学进展,已发展出了有防范能力的算法和实现
3. 第三个原因和异或运算的运算特点有关,也就是相同的数据归零,不同的数据归一:
a. 归零律
如果两段数据完全相同,它们的异或运算结果,就是每一位都是零的数据;
b. 恒等律
和零进行异或运算,不改变原数据的数值。
备注
正是异或运算的归零律和恒等律,CBC 模式才能成立,解密才能进行。这两个性质,还使得解密运算和加密运算具有相同的运算效率。然而,CBC 模式的主要安全问题,也来源于异或运算的这两个性质。
【攻击方法】:如果两段数据中只有一位不同,它们的异或运算结果,就是只有这一位的数据是一,其他的数据都是零:
一个 128 位的密钥,它的强度能承受 2^128 次的运算,是一个强度的指数级别的量级。
1. 如果我们一次改变一位数据的攻击方式得逞,最多需要 128 次的运算;
2. 如果我们一次只能观测一个字节,一次一位的改变需要 2^8 = 256 次(一个字节有8位)
这样的攻击方式得逞,最多需要 255 * 16 = 4080 次的运算(一个数据分组16个字节)
这样的运算强度,和设计的理论值 2^128 相差太远了,一次有效的破解也就是分分钟的事情。
【防范攻击方法】:阻断一个攻击的方式之一,就是破坏攻击依赖的路径或者条件。对于上面的攻击方式,其实只要攻击者没有办法一次改变一位数据或者少量的数据,这样的攻击就可以被有效破解了。也就是要保证攻击者在展开攻击的时候,没有办法一次改变不少于一个数据分组的数据。对于 AES 来说,数据分组大小是 128 位,攻击者需要运算 2^128 次,才可以攻击得逞。
【防范攻击具体方案】密文分组、密钥、加密算法、解密算法,这些都是固定的数据或算法,没有考量的空间。剩下的变量,就只有明文分组和初始化向量了。要想解决掉这个安全问题,关键在于该怎么控制明文分组和初始化向量。
密钥少一位会有影响吗¶
少一位密码,当然会带来计算性能的差异,以及由此引发的计算时间偏差。可是,似乎 2020 年之前,没有人担心这件事。直到 2020 年 9 月 8 日,一个名字叫做“浣熊攻击”的安全研究成果发布了。浣熊攻击可以利用密钥高位清零造成的运算时间差,通过观察、测算运算时间,运用统计学的技术破解运算密钥。这实在是一个了不起的发现。
目前来看,这种攻击方式还比较复杂,不容易执行。但是,一旦发现攻击方法,如果业界没有采取及时的措施,攻击技术的改进速度是惊人的。“浣熊攻击”出现,再一次敲了敲大门,警告我们要尽量避免计算时间偏差和计算算力偏差,谨慎地处理不可避免的计算时间偏差和算力偏差。
思考¶
调用它的对称密钥生成接口,试着产生很多 128 位的密钥。你看一看,有没有可能返回 127 位或者 129 位的密钥。 如果你找到了不是 128 位的密钥,这个算法库就有潜在的安全问题。
生成一对 1024 位 RSA 非对称密钥,用公钥加密大量的 1024 位的不同数据,然后用私钥解密这些数据,统计解密消耗的时间。如果解密时间不是大致相同的,这个 RSA 实现就是有问题的。破解起来可能就是分分钟的事情。这是一个让我们了解计算时间偏差和计算算力偏差的练手题,也是个常见的分析 RSA 实现漏洞的攻击办法。
Timing Attack本地写了代码尝试,果然很神奇。java里的String的equals方法是按照字符一个个顺序匹配的,直到碰到不一样会返回。java.lang.String#equals碰到大量分批次有目的破解时,找到每轮中耗时最少出现次数最多的那个值。这样子依次就破解了每个字符。后来改用java.security.MessageDigest#isEqual,就破解不出来了。 一个攻击方式 timing attack,如果采用不安全的字符串比较方式 可以通过执行比较的时间 进而推断出待比较的内容 比如密码(口令)等。只要是涉及到秘密的运算,都要考虑计算的时间偏差和算力偏差。
软件使用过硬件运转的,比如如果计算复杂,CPU就会加快,温度会升高,风扇会加速,噪音也会加大,计算结果会延迟,这些都是外部可以观察到的结果。感兴趣细节的话,可以看看这篇报道,https://threatpost.com/side-channel-poc-attack-targets-encryption-software-glitch/136703/,以及https://www.usenix.org/system/files/conference/usenixsecurity18/sec18-alam.pdf,还有这个https://www.cs.tau.ac.il/~tromer/papers/radioexp-20150227.pdf
11 | 怎么利用解密端攻击¶
备注
CBC 算法要被扫进垃圾箱的主要原因,就是因为这个算法太难用对了
怎么利用解密端攻击¶
备注
针对解密端的攻击,最常见的方式,就是给定密文数据,观测解密运算是成功还是失败。
解密端是怎么知道解密是成功还是失败呢?可以利用「数据补齐方案」。
数据怎么补齐¶
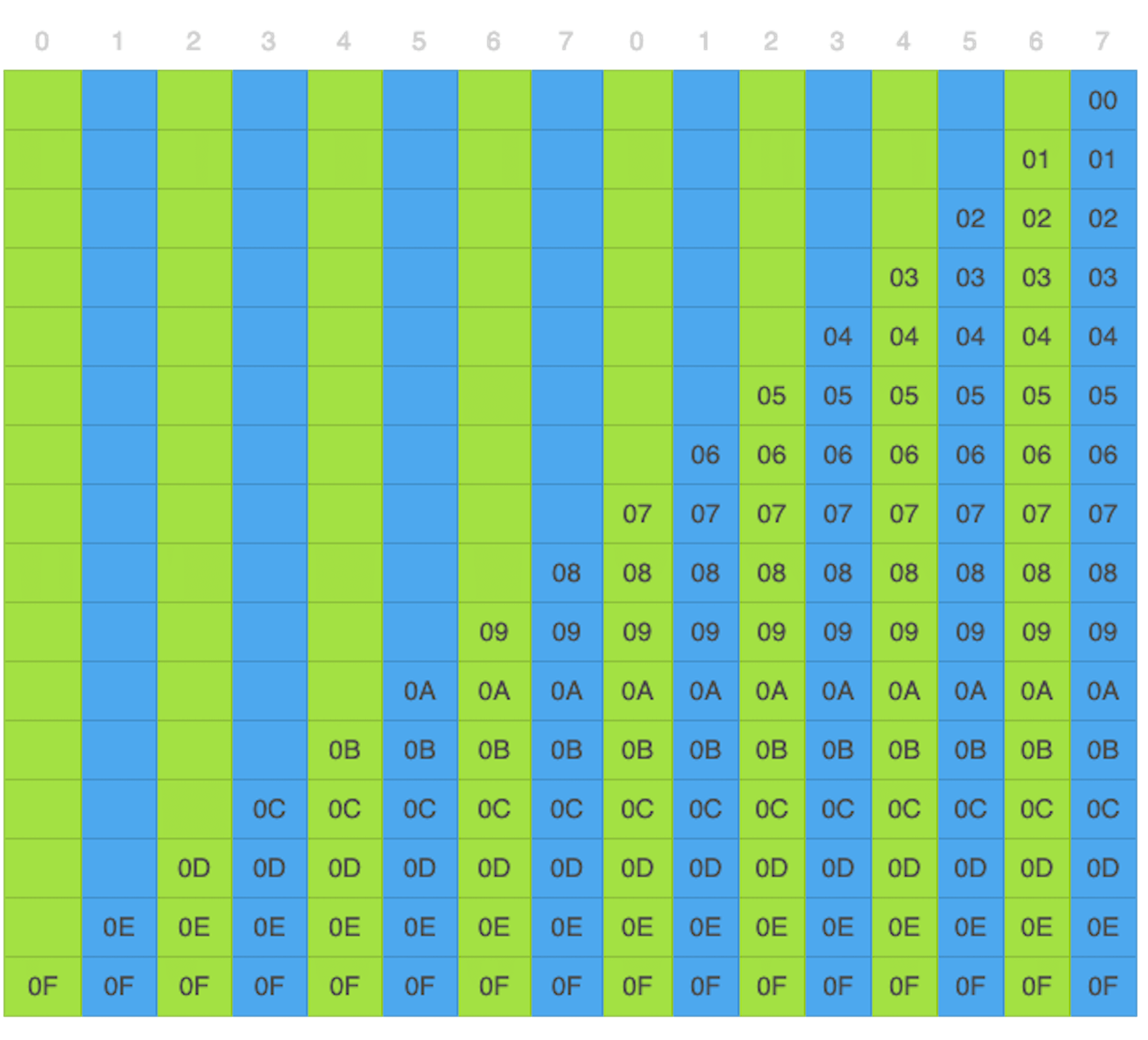
有标识字节的数据补齐方案:如果一段数据只有 15 个字节,补齐的数据就只有这个标识字节,数值为 0,表示没有额外的补齐数据;如果有 14 个字节,标识字节为 1,表示还有一个字节的额外补齐数据,额外的补齐数据的数值也是 1;如果有 13 个字节,标识字节为 2,表示还有两个字节额外补齐数据,额外的补齐数据的数值也是 2;以此类推。需要注意的是,如果一段数据有 16 个字节,也就是刚好一个数据分组大小,这时候,就需要一个全是补齐数据的数据分组,它的每一个字节都是 15。¶
攻击怎么展开¶
破解最后一个字节¶
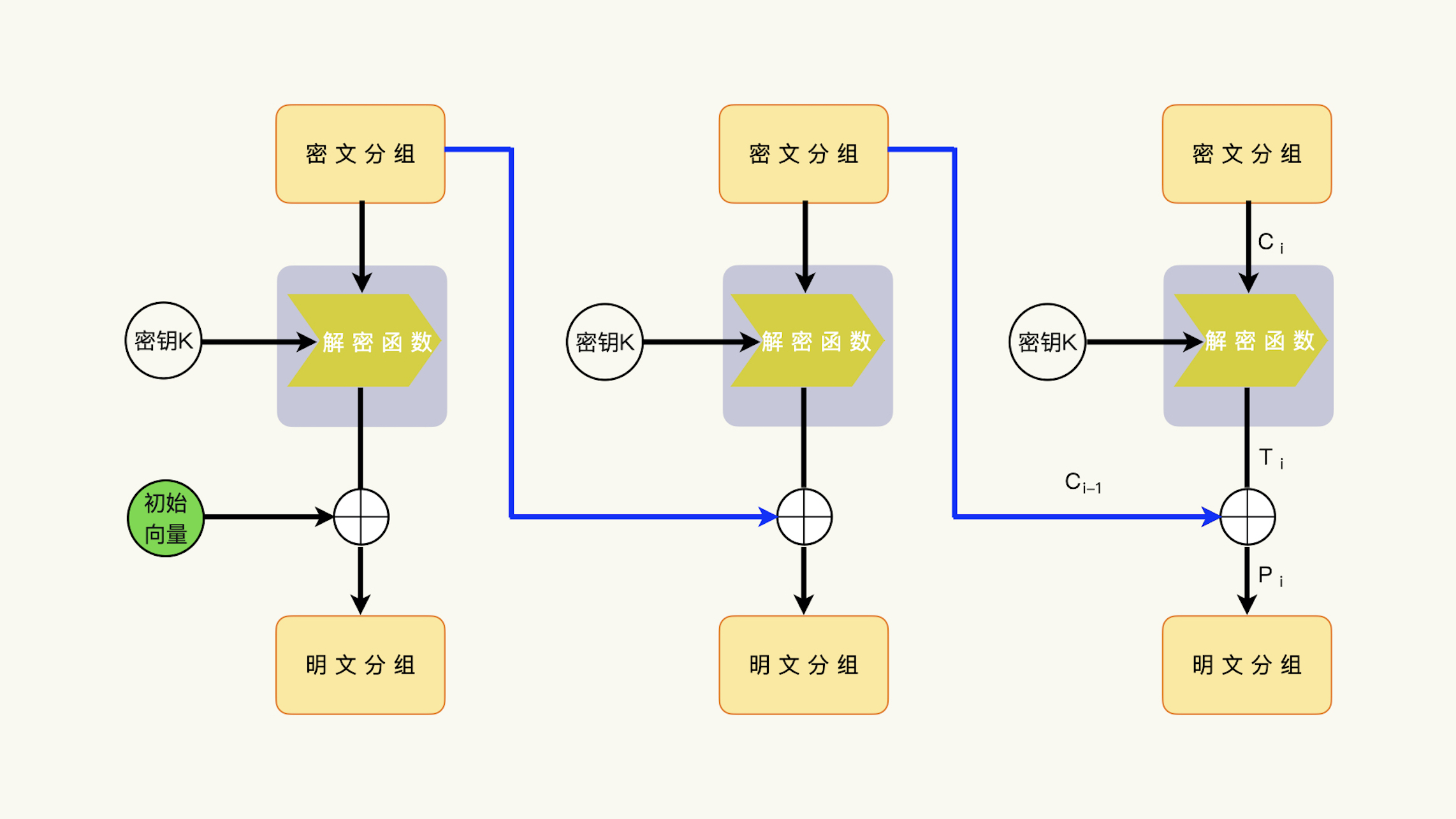
一个密文分组的解密,需要如下的输入数据: 1.上一次的密文分组 Ci-1; 2.这一次的密文分组 Ci; 3.加密和解密共享的密钥 K。密文分组 Ci 和密钥 K,通过解密函数的运算,可以产生一个中间结果 Ti;然后,解密函数运算结果 Ti 和上一次的密文分组进行异或运算,获得明文分组 Pi,Pi = Ci-1 ^ Ti。¶
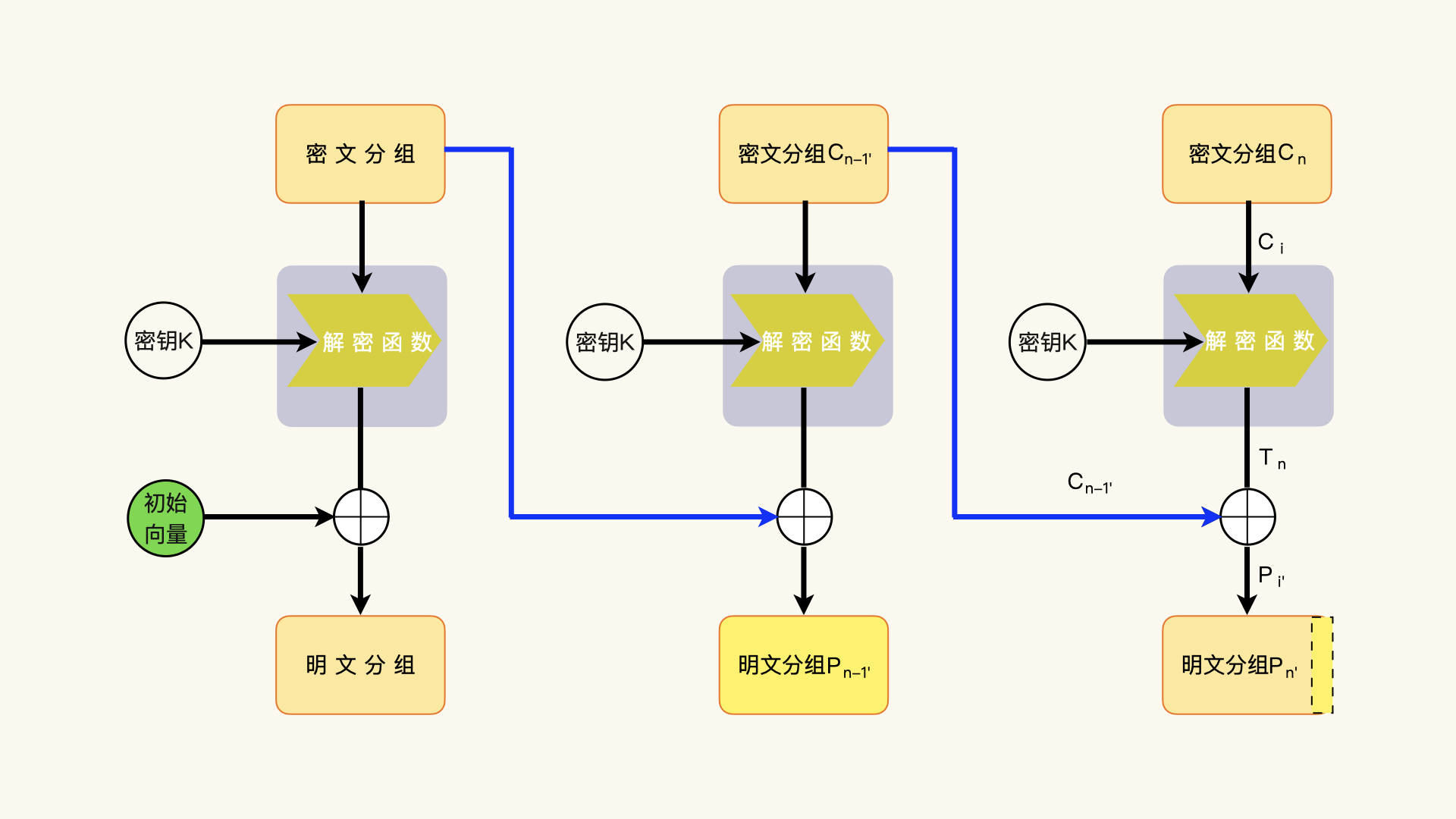
利用数据补齐方案的攻击,通过修改、构造最后一个密文分组 Cn 的前一个密文分组 Cn-1,也就是倒数第二个密文分组,然后让解密端解密构造后的密文数据,观察修改了密文数据的解密能不能成功。¶
备注
倒数第二个密文分组构造原理:解密端并没有办法知道这一个密文分组是否解密失败。要判断解密是否成功,需要解密后判断最后一个明文分组的补齐数据是不是符合规范。补齐数据的校验就会失败,解密端就会报错。观察解密端的行为,攻击者就能了解到,这个构造的字节没有通过解密过程。
如果我们修改倒数第二个密文分组的最后一个字节,那么解密后的最后一个明文分组应该只有最后一个字节受到影响。如果这个解密后的字节是零,其他的数据会被解读为有效数据,这样就会通过补齐数据的校验。如果这个解密后的字节是其他数值,补齐数据的校验通过的概率就很小。实际的攻击过程,这么一点小小的概率也可以优化过滤掉。
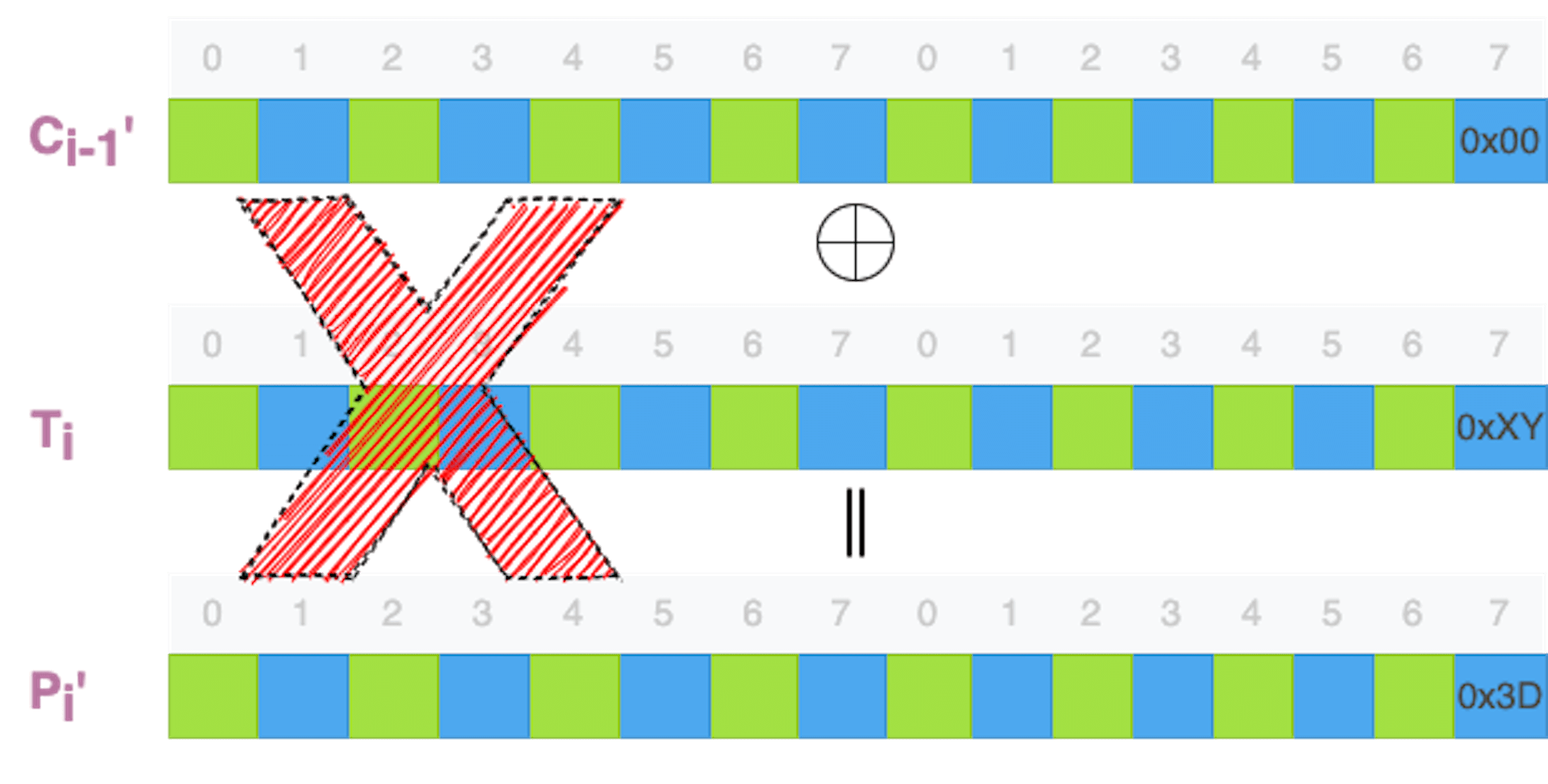
如果解密后的这个字节不是零,那么,补齐数据的校验就会失败,解密端就会报错。攻击者就会调节最后一个字节的数值,比如数值加一,然后再次让解密端尝试解密。¶
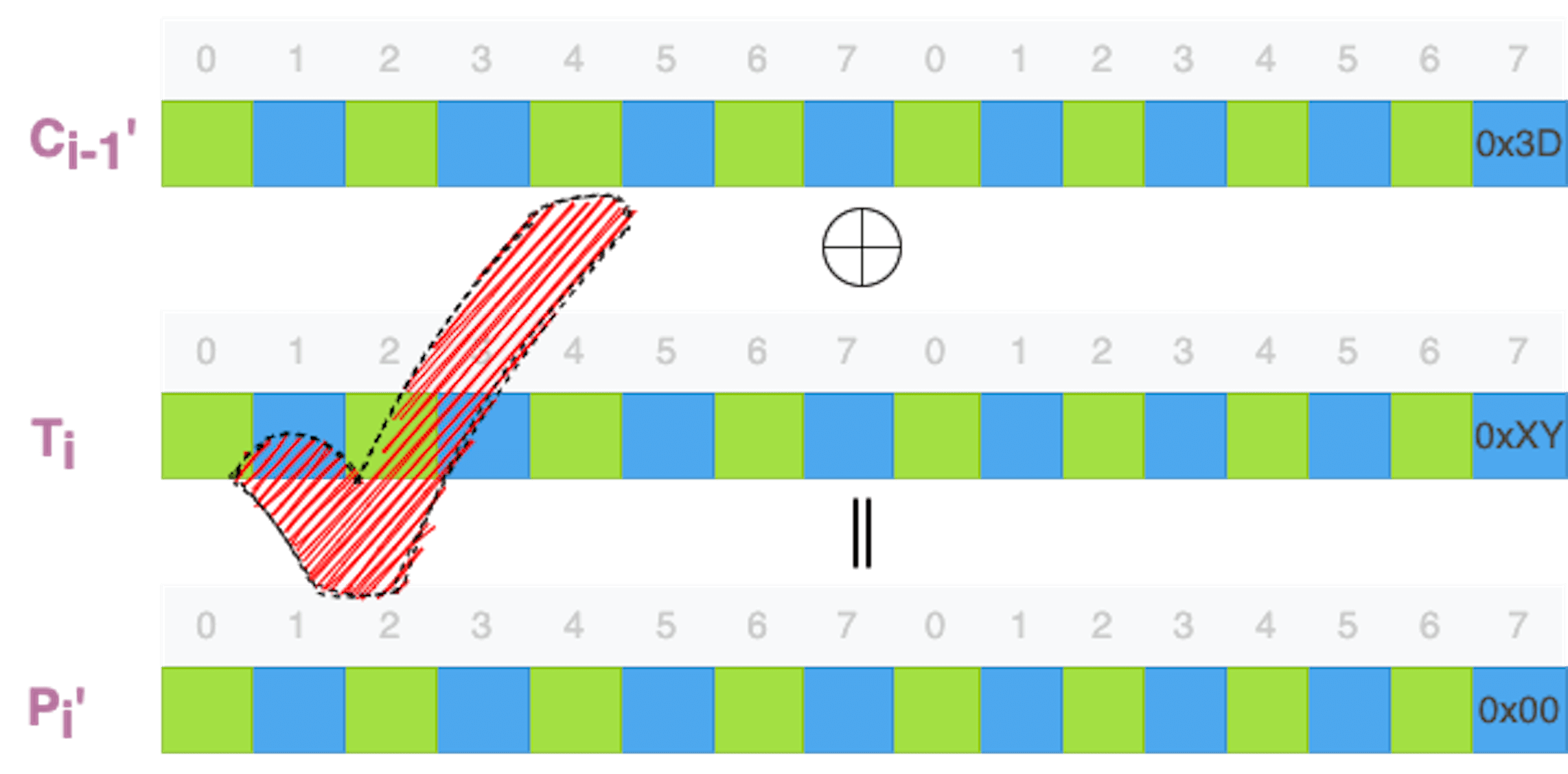
一个字节只有8位,256 种可能性,最多尝试 255 次,一定会有一次尝试,补齐数据是零。¶
当攻击者观察到解密成功时,他能够掌握哪些数据呢?他能够直接得到的数据包括:
1. 未修改密文分组的最后一个字节的数值(Cn-1[15])
2. 修改后密文分组的最后一个字节的数值(Cn-1'[15])
3. 解密端明文分组的最后一个字节的数值(Pn'[15],就是 0x00)
通过计算,解密函数运算结果的最后一个字节的数值(Tn[15]):
> Pn'[15] = Tn[15] ^ Cn-1'[15]
> =>
> Pn'[15] ^ Cn-1'[15] = Tn[15] ^ Cn-1'[15] ^ Cn-1'[15] = Tn[15]
真正的明文字节也就被破解出来了:
> Pn[15] = Tn[15] ^ Cn-1[15]
备注
非常简单的运算,运算次数不多于 255 次,攻击者就破解了一位字节。
破解倒数第二位字节¶
备注
破解倒数第二位字节,要使用的补齐数据是一(0x01)
计算、修改上一次的密文分组的最后一个字节,使得解密后的明文分组的最后一个字节是0x01:
> Tn[15] ^ Cn-1'[15] = 0x01
> =>
> Tn[15] ^ Cn-1'[15] ^ Tn[15] = 0x01 ^ Tn[15]
> Cn-1'[15] = 0x01 ^ Tn[15]
备注
这样,解密端就确认了最后一个字节是一,也就是补齐数据的标识字节是一。只要倒数第二个字节也是一,补齐数据的检验就通过了。倒数第二个字节破解方式和第一个字节的破解方式相同。
每个字节的破解,运算次数都不会多于 255 次。从倒数第一位开始,依次破解,直到第一个字节破解结束,总的计算量是 255 乘以字节数。对于 AES 而言,一个数据分组有 16 个字节,破解计算只需要 255 * 16 = 4080 次。这么小的破解计算量,是没有什么安全性可说的。预测补齐数据的这一类破解方案,都可以叫做“补齐预言攻击”。2002 年,塞尔吉·沃德奈(Serge Vaudenay)公布了补齐预言攻击。
阻断补齐预言攻击的办法¶
方法1:和数据完整性校验的算法结合起来,而不是依赖补齐数据是否合法,来判断解密数据是不是有效
方法2:每一次加密 / 解密计算,都使用初始化向量
12 | 怎么利用加密端攻击¶
怎么利用加密端攻击¶
一个明文分组的加密,需要如下的输入数据:
1. 上一次的密文分组 Ci-1或初始化向量
2. 这一次的明文分组 Pi
3. 加密和解密共享的密钥 K
这一次的明文分组 Pi 和上一次的密文分组 Ci-1 进行异或运算,获得中间结果 Ti:
Ti = Ci-1 ^ Pi
然后,Ti 和密钥 K,通过加密函数的运算,产生密文分组:
密文分组 Ci
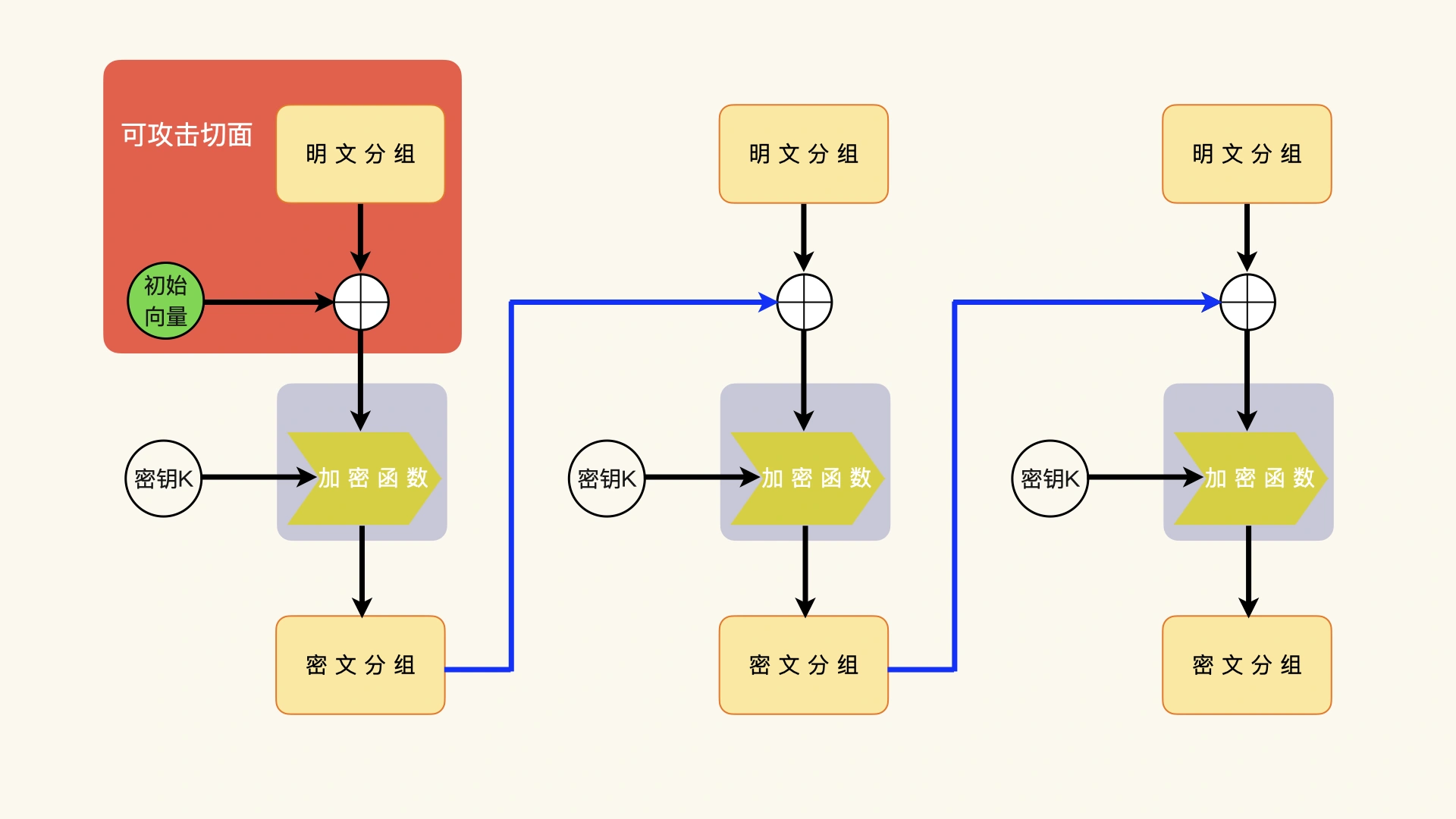
加密端的异或运算,发生在明文分组和上一次的密文分组(对于第一次运算,上一次的密文分组就是初始化向量)之间。针对加密端的攻击,同样,我们也是在明文分组和上一次的密文分组或者初始化向量上想办法。¶
备注
【疑问】初始化向量是不是每次加密的第一个都会用?
攻击理论上可行吗¶
前提:
攻击者可以使用加密接口
攻击者可以知道:
上一次密文分组 Ci-1
这一次的密文分组 Ci
假设已知目标明文分组是 Pi’,则:
Ti' = Pi' ^ Ci-1
Ci' = Ek(Ti')
所以如果构造出一个Pi使上面操作的 Ci' 的值为真实密文分组 Ci 相同,则:
Ci = Ci'
对于 AES 算法来说,一个明文分组 Pi 有 16 个字节,也就是 128 位。如果一位一位地尝试,需要 2^128 次运算。这种数量级的运算,现在的计算能力还是无能为力的。
攻击实践上可行吗¶
备注
假设攻击者已经知道了明文分组里的 15 个字节,只剩下最后一个字节未知。攻击者按照上述的构造明文分组的方式,他最多尝试 2^8-1=255 次,最后一个字节就可以破解了。
现实:
网络里的数据,大部分都是格式化的,比如 HTTP 的数据
HTTP Header、HTTP 的请求内容大部分是重复的
(除了Cookie、手机号、验证码私有数据外)
所以,攻击者知道 15 个字节,甚至整个明文分组,这种情况在实际中,是经常出现的。
如果手机验证码的第一个字节刚好是一个明文数据分组的最后一个字节。如果手机验证码的第一个字节不是明文数据分组的最后一个字节,该怎么办?思路也很简单粗暴,只要我们想办法把手机验证码的第一个字节挪到明文数据分组的最后一个字节就行。该怎么操作呢?也很简单,通过更换顺序、删减或者增加手机验证码的前面的字节,就可以了。
备注
2011 年 9 月,两位天才般的研究人员(Juliano Rizzo,Thai Duong)公开了上述的攻击方案。并且表示,只要给他们几分钟时间,他们就可以利用该漏洞入侵你的支付账户。他们给这个攻击技术取了一个超酷的名字,叫做 BEAST。
有什么防范措施¶
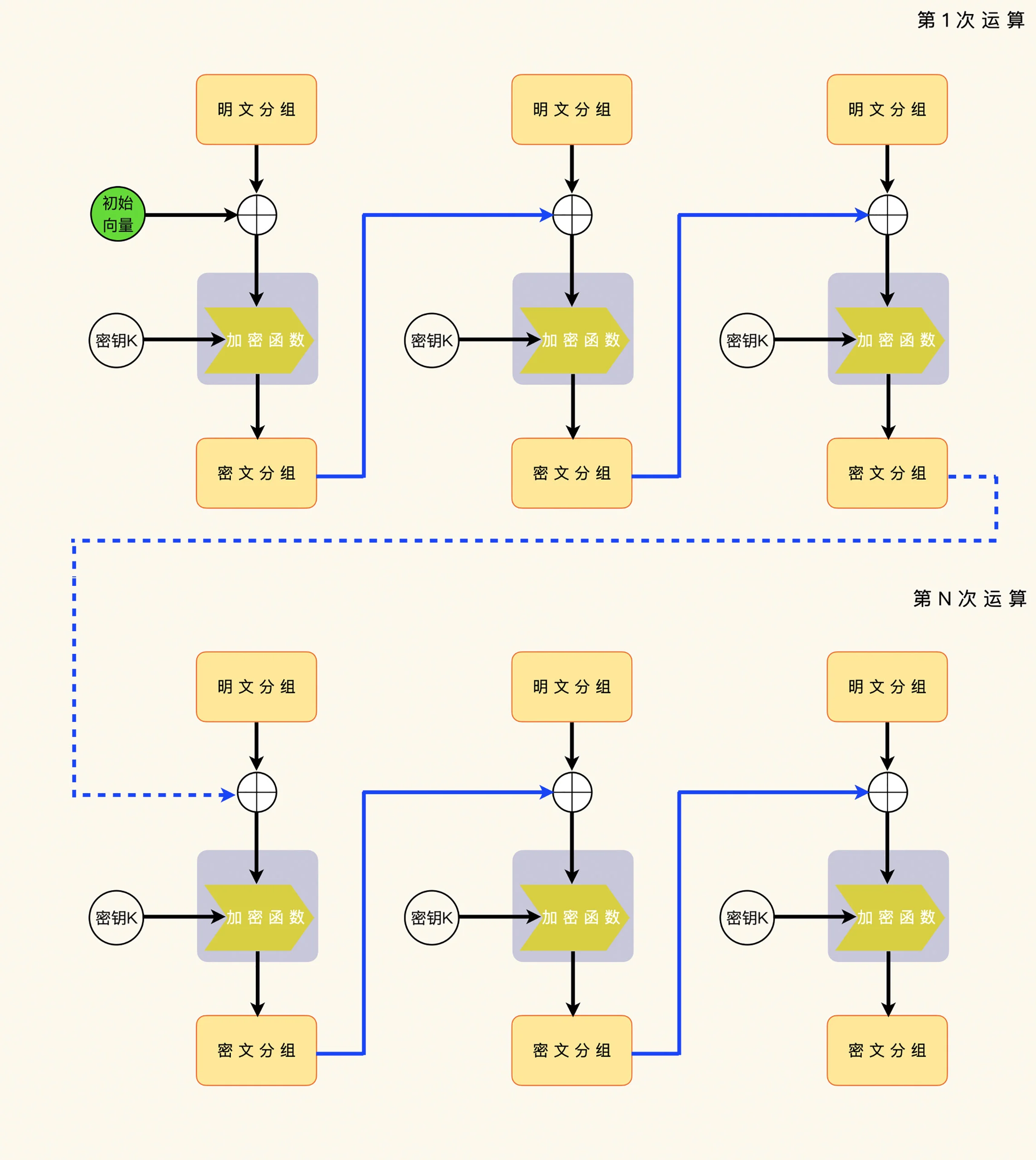
防范措施还是要在初始化向量上想办法。BEAST 攻击起作用的关键,就是要使用上一次加密运算的最后一个密文分组。如果这一次的加密运算不使用上一次加密运算的数据,BEAST 攻击就无法运算了。¶
和防范补齐预言攻击的办法一样,替换的办法就是每一次加密运算,都使用不同的初始化向量。比较麻烦的是,对于每一次解密运算,解密端需要加密端使用的初始化向量,然后才能执行解密运算。¶
改进的防范措施¶
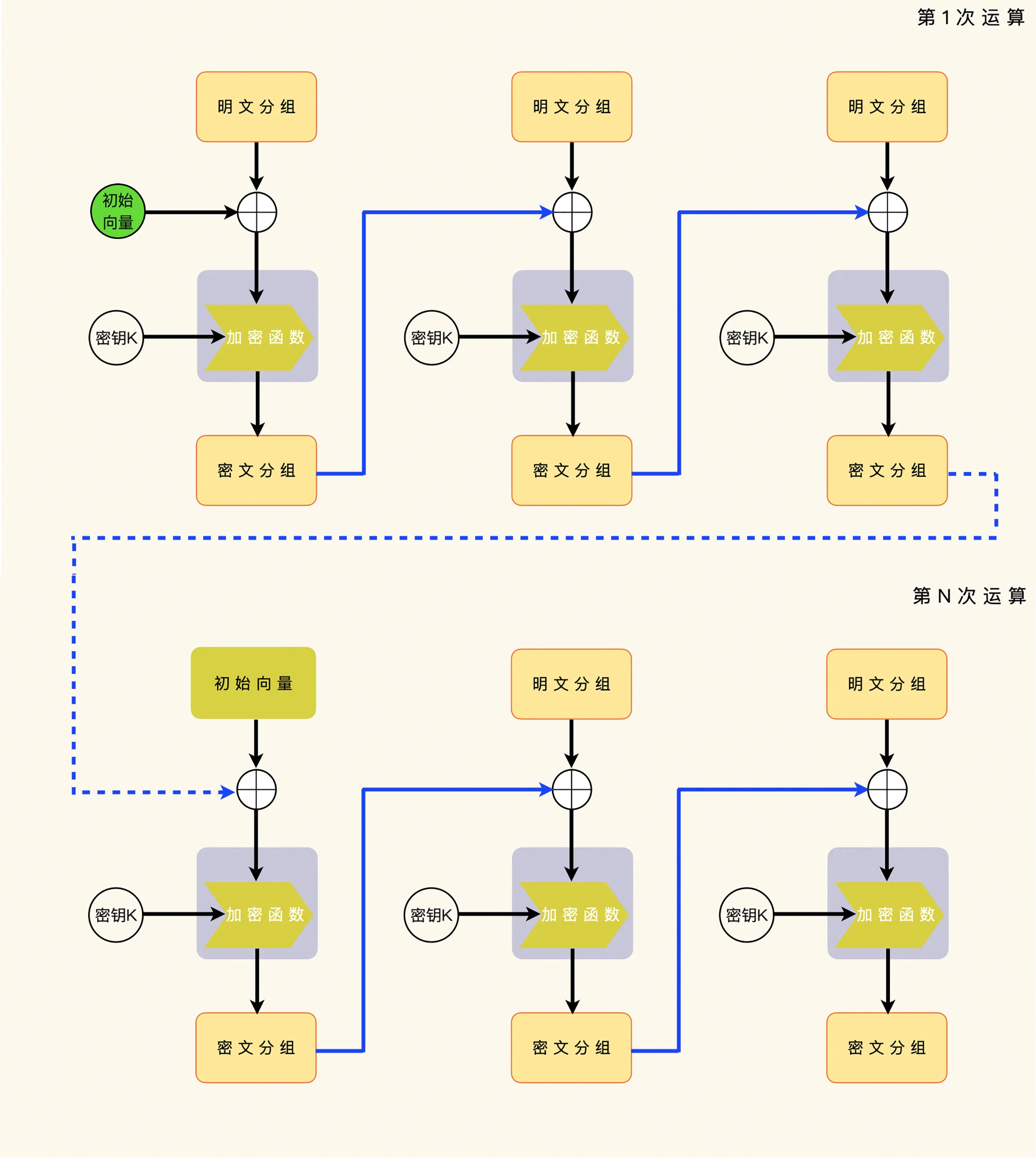
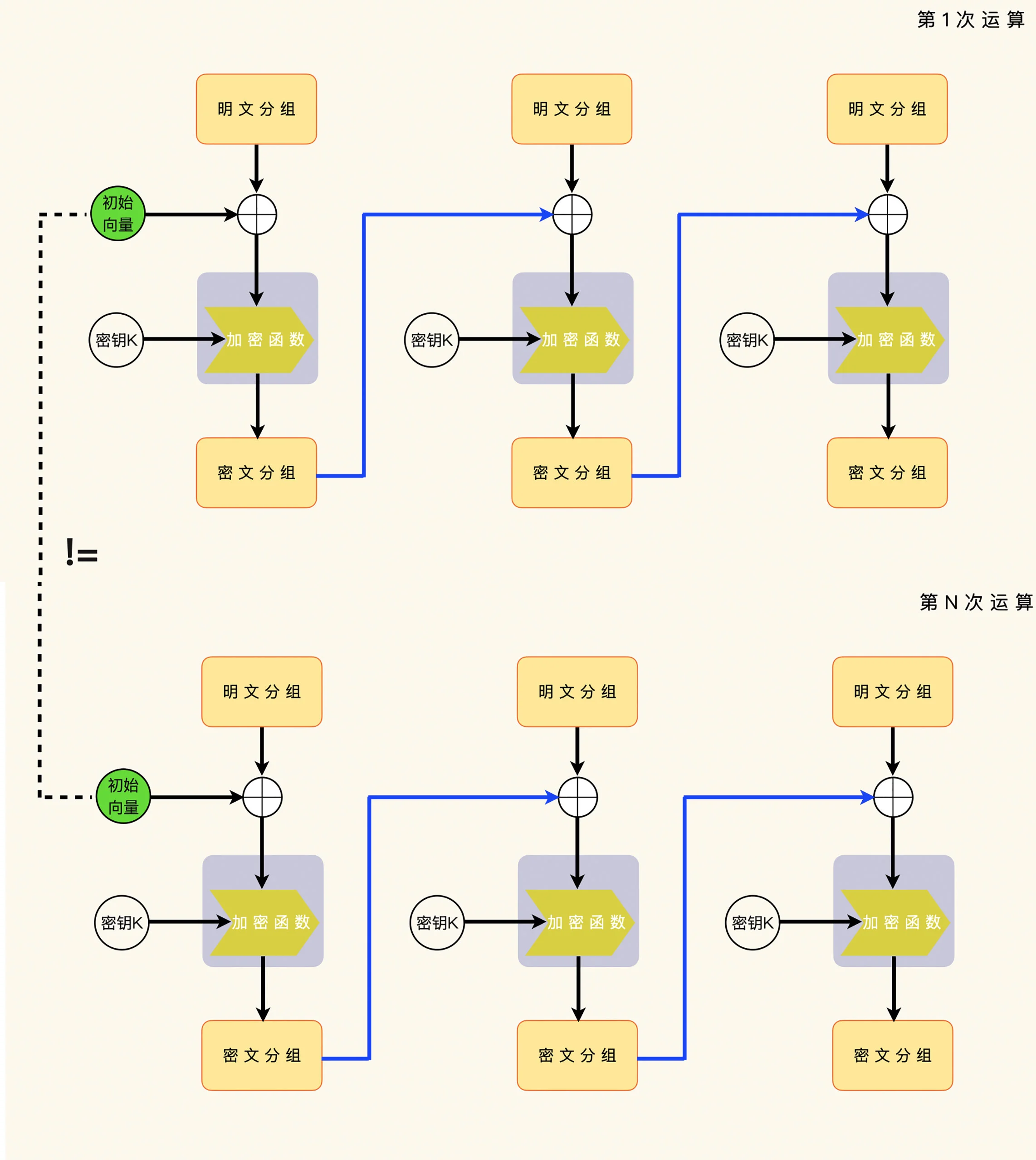
一个改进的办法,就是继续使用上一次加密运算的最后一个密文分组,同时把每一次运算的初始化向量当做第一个明文分组来处理。¶
这个办法的好处,就是解密端不需要知道加密端选择的初始化向量,就可以执行解密运算。这个办法的坏处,就是解密端需要丢掉初始化向量这一段数据,不能把它当做应用数据来处理。
13 | 如何防止数据被调包¶
怎样有效地验证一段信息¶
有额外的信息
验证信息和待验证的消息之间要有关联
验证信息的计算要快,数据要小
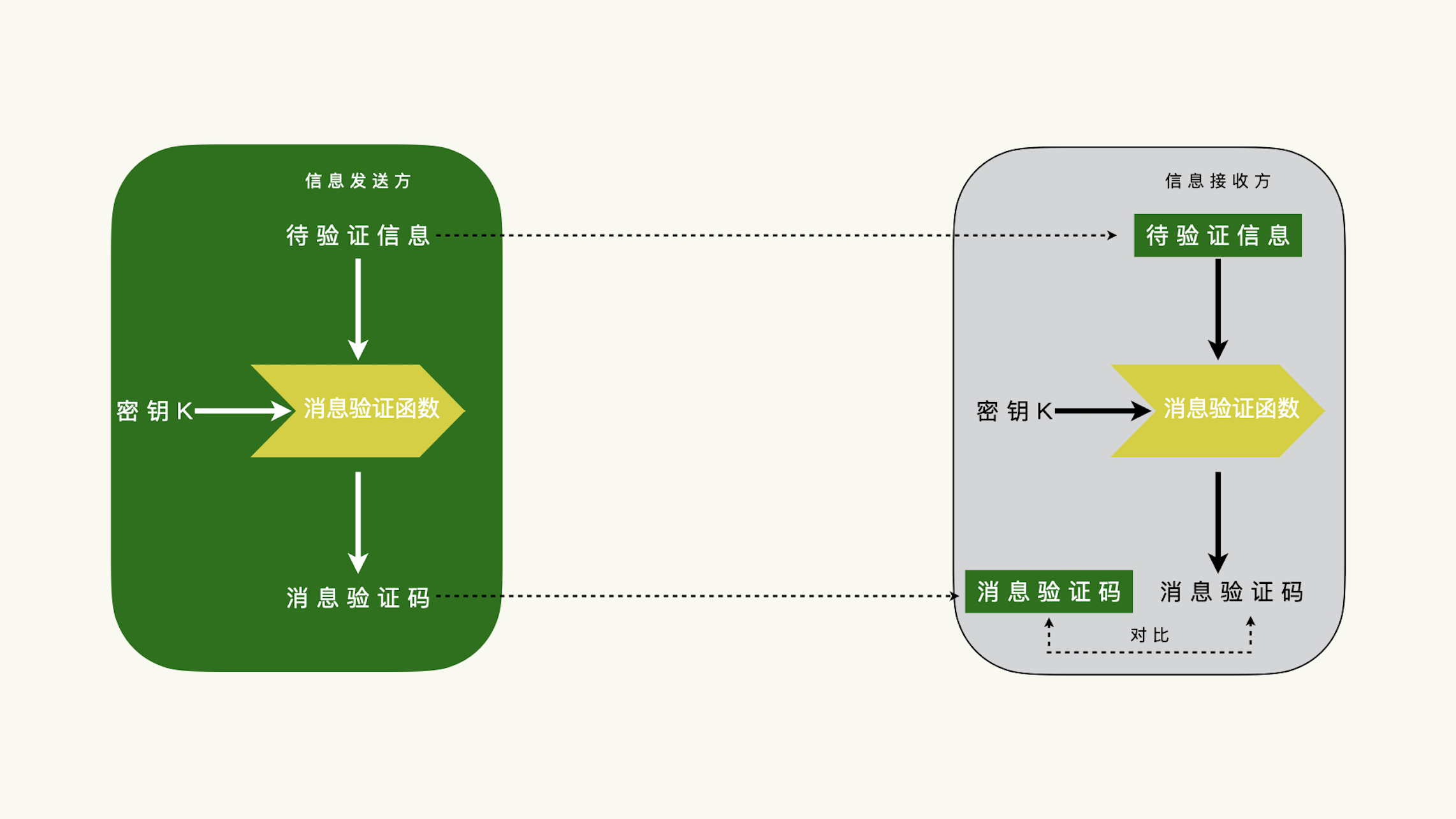
消息验证码(Message Authentication Code, MAC)¶
该怎么选择消息验证函数¶
最常见的方案就是:基于单向散列函数的消息验证码(Hash-based Message Authentication Code, HMAC)
在 HMAC 的算法里,单向散列函数的输入数据是由对称密钥和待验证消息构造出来的。对称密钥的参与,是为了确保散列值来源于原始数据,而不是篡改的数据。
备注
从1997 年发表的 RFC 2104 到目前为止,这种构造方法还没有明显的安全问题
严格的来说,HMAC 算法的安全强度,是由对称密钥的安全强度和两倍的散列值长度之间较小的那个数值决定的。一般来说,两倍的散列值长度通常大于流行对称密钥强度。所以,HMAC 算法的强度,通常也是由对称密钥决定。简单起见,对于流行的 HMAC 算法,我们只需要考虑对称密钥的安全强度。
备注
这儿说 两倍的散列值长度 是和HMAC算法的构造有关系,两倍弹列值长度以内的数据,理论上不能构造出碰撞的数据,两倍以外就没办法保障了。 详细的算法,你可以看看RFC 2104里的描述。
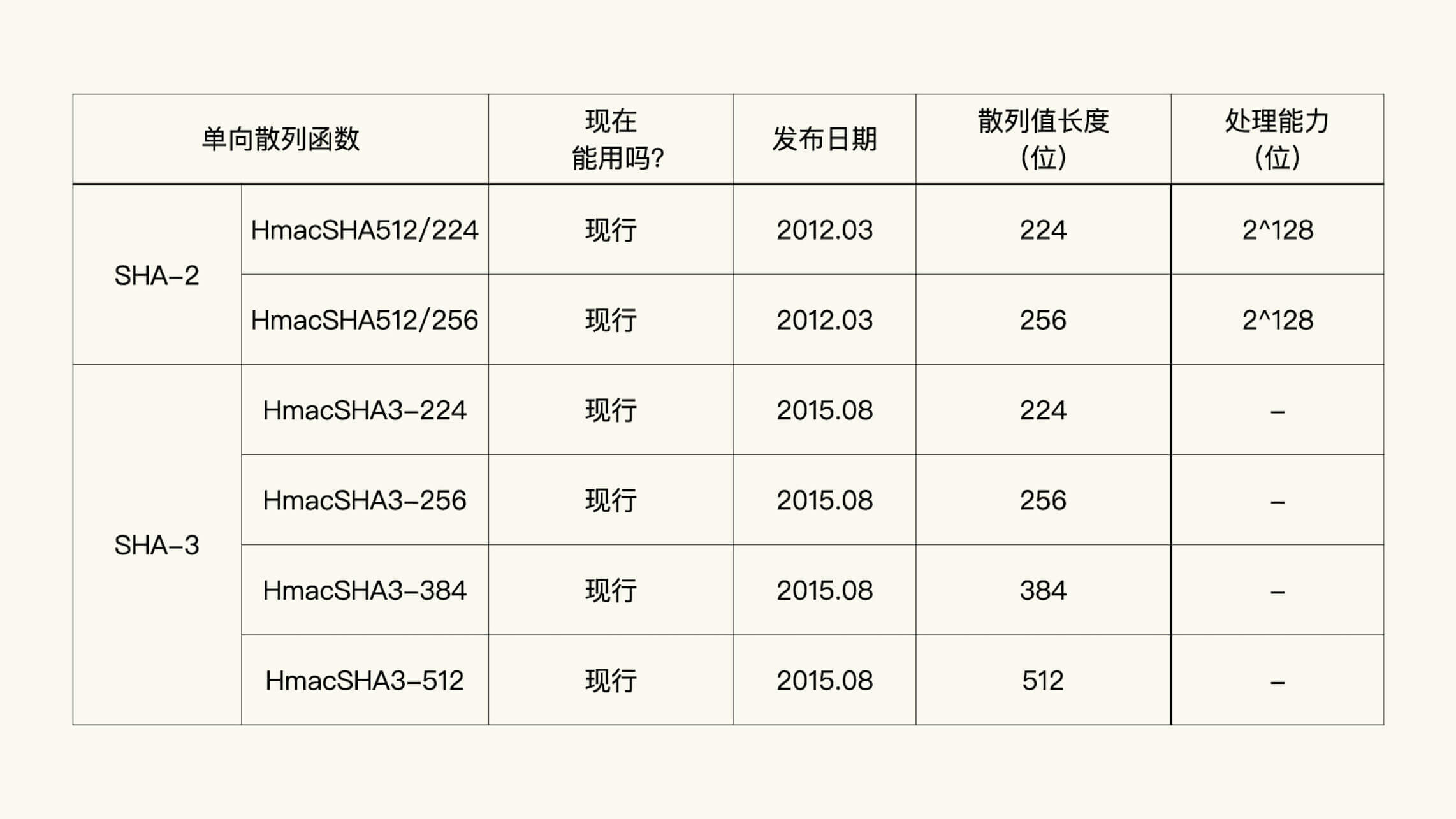
有哪些常见的 HMAC 算法¶
HMAC 算法是由单向散列函数的算法确定的。
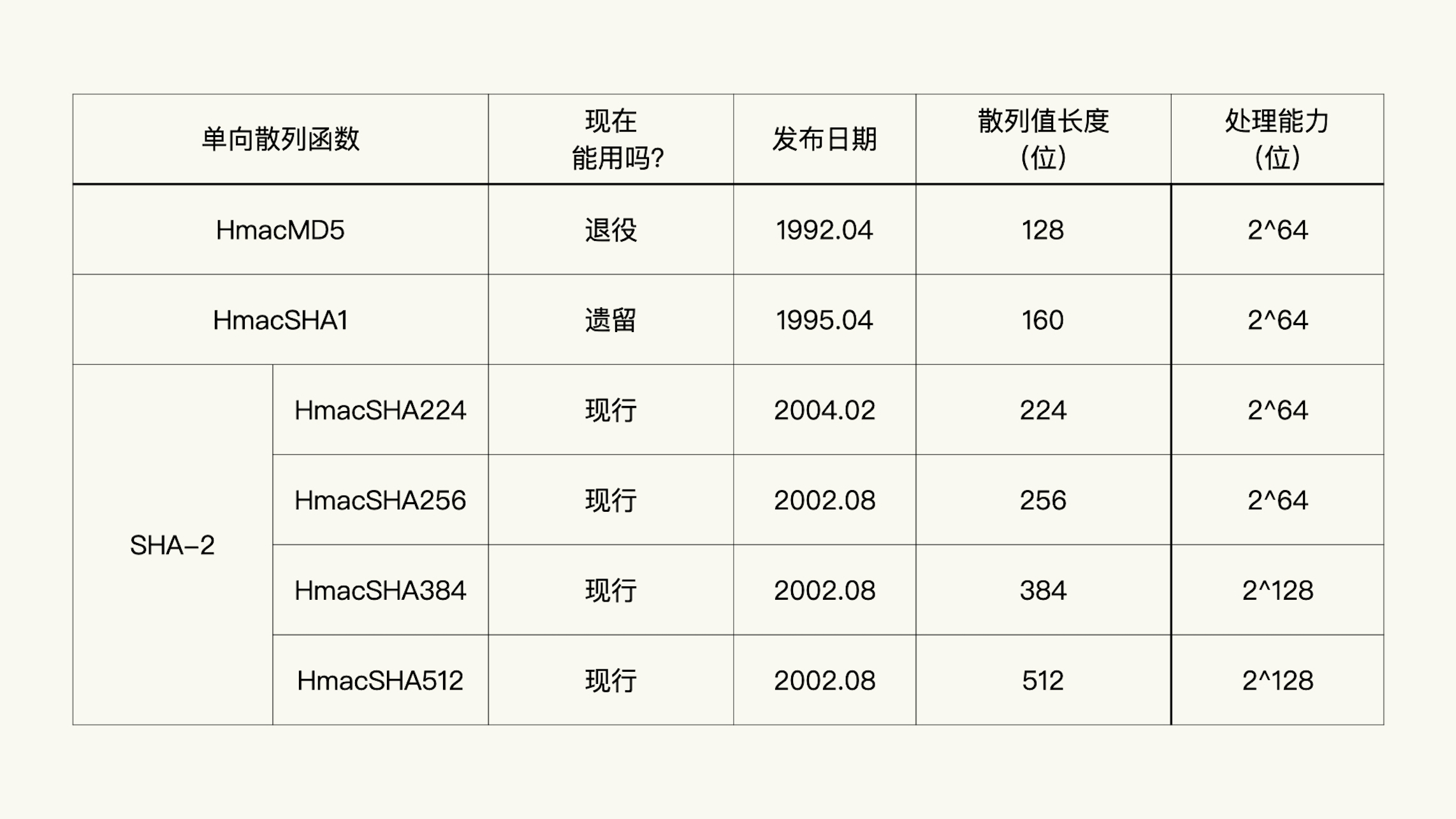
其中,HmacSHA256 和 HmacSHA384 是目前最流行的两个 HMAC 算法。¶
参考文献¶
HmacMD5:RFC 1321
HmacSHA1:FIPS 180-1
HmacSHA224:FIPS 180-3
HmacSHA256、HmacSHA384、HmacSHA512: FIPS 180-2
HmacSHA512/224、HmacSHA512/256 :FIPS 180-4
HmacSHA3-224、HmacSHA3-256、HmacSHA3-384、HmacSHA3-512:FIPAS 202
其他¶
生成6位数字的双向验证软件,其实就是对当前时间进行hmac。因为时间这个原数据客户端和服务端都是一样的,所以hmac也应该是一样的。双向验证软件(two factor),比如Google身份验证器等,都会把epoch分段,然后在加上一点容错。这样即使客户端在提示的30s快到的时候输入验证码,服务端也会认证通过。 如果手动改变手机时间,双向认证软件会工作不正常。
14 | 加密数据能够自我验证吗¶
先加密还是后加密¶
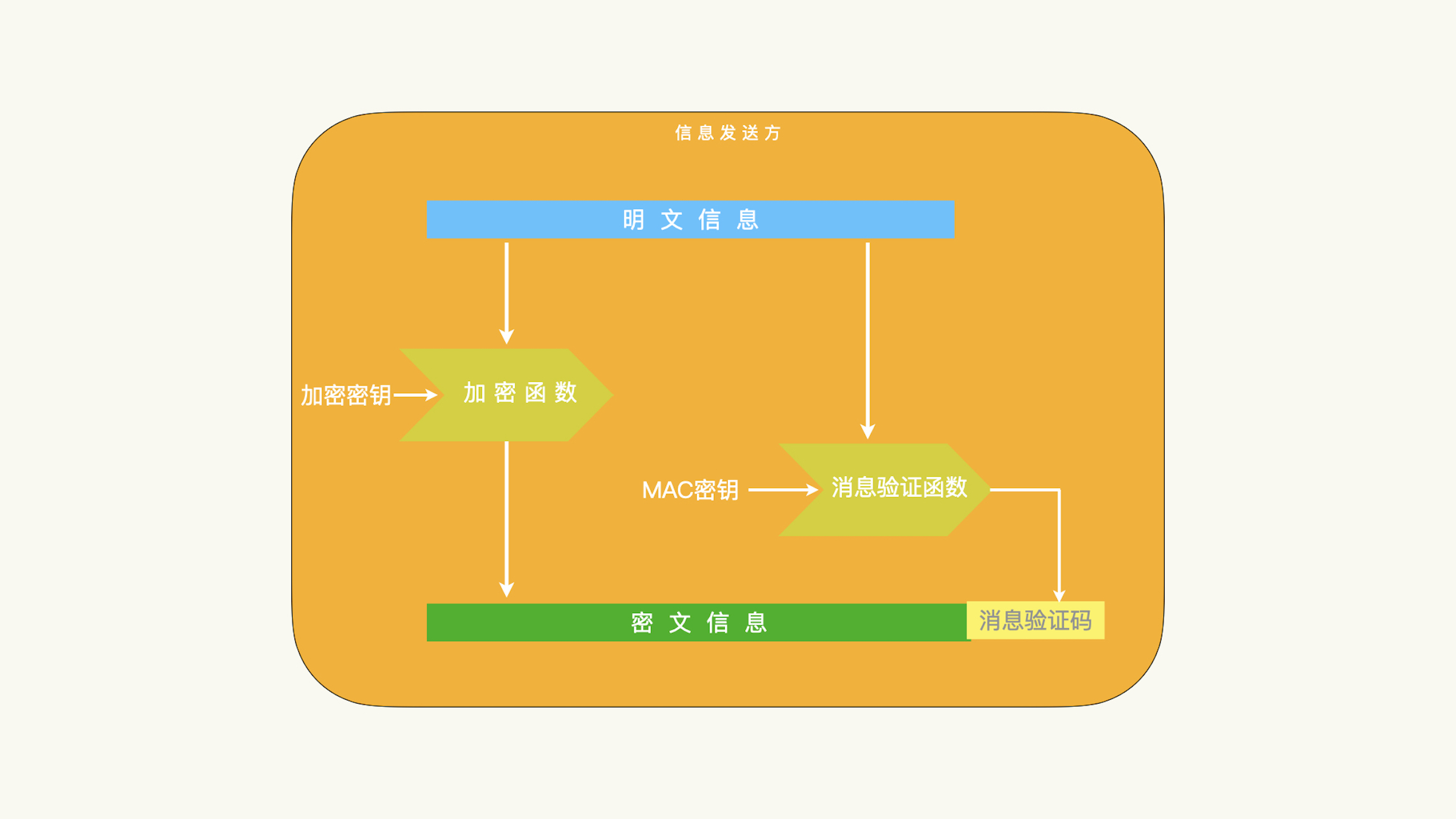
加密并验证:安全外壳协议(SSH)就是采用加密并验证的方案¶
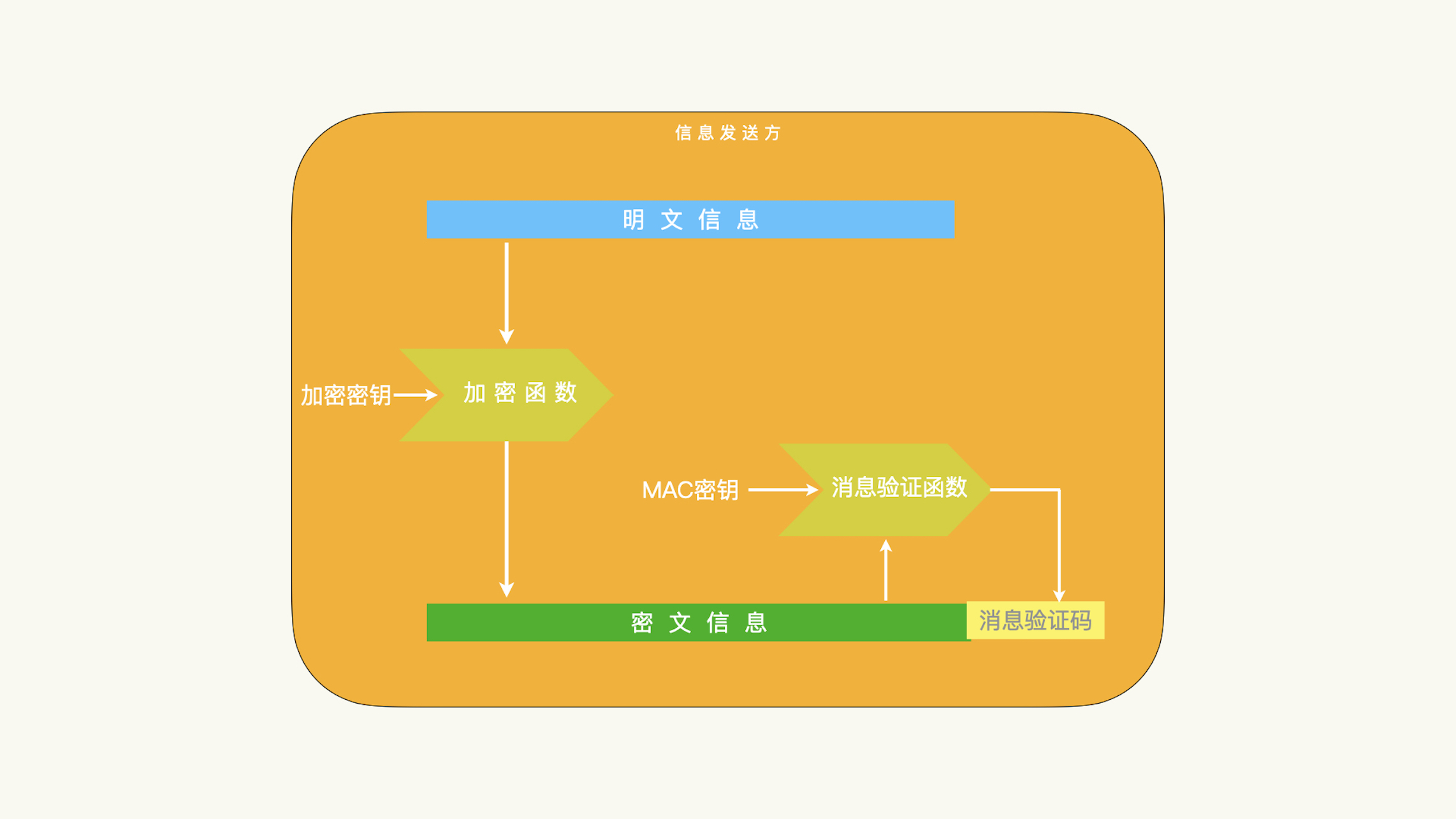
加密后验证:IPSec 协议采用的就是加密后验证的方案。¶
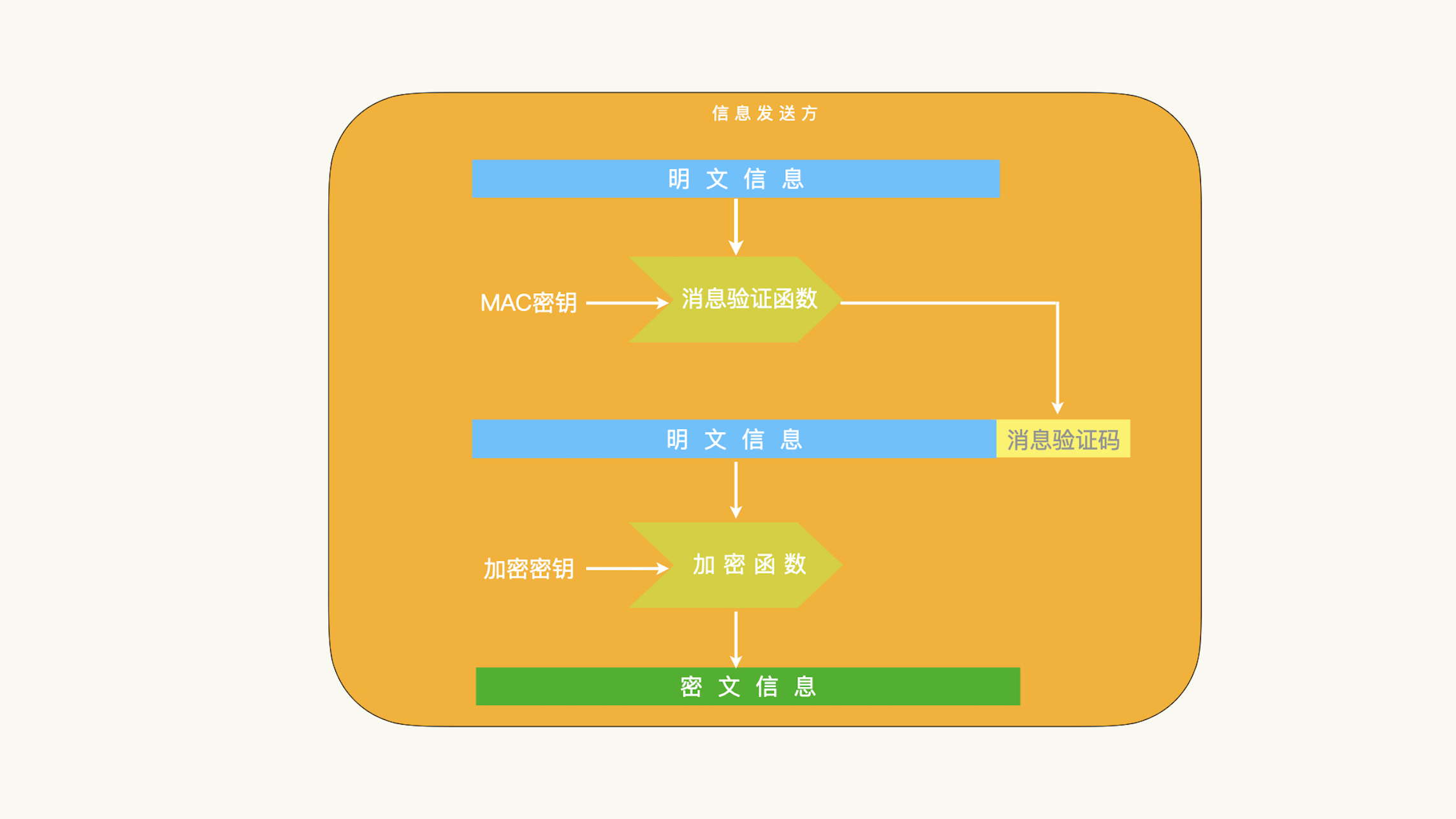
验证后加密:SSL 协议采用的就是验证后加密的方案。¶
备注
「加密并验证」和「验证后加密」都是保护的明文信息的完整性;而「加密后验证」保护的是密文信息的完整性。针对 BEAST 攻击这种新技术的攻击,针对明文信息完整性的保护都受到了很大的挑战和质疑。所以,如果我们只能从上述三个方案中间选择,加密后验证这个方案目前来说,是最安全的方案。
带关联数据的加密¶
带关联的认证加密(Authenticated Encryption with Associated Data(AEAD))
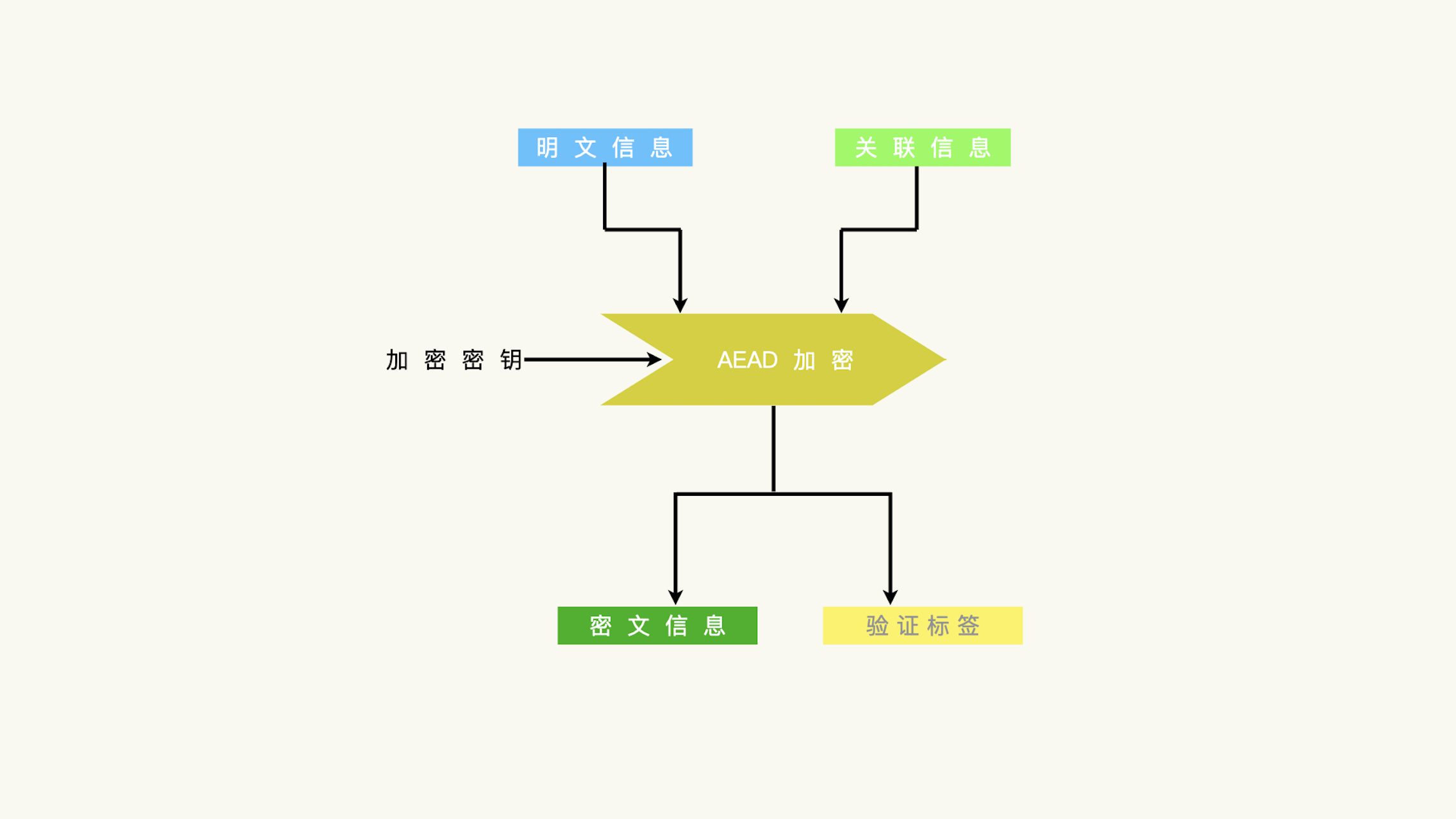
加密函数需要三个输入数据: 1.加密密钥 2.明文信息 3.关联信息。输出结果包含两段信息: 1. 密文信息 2. 验证标签¶
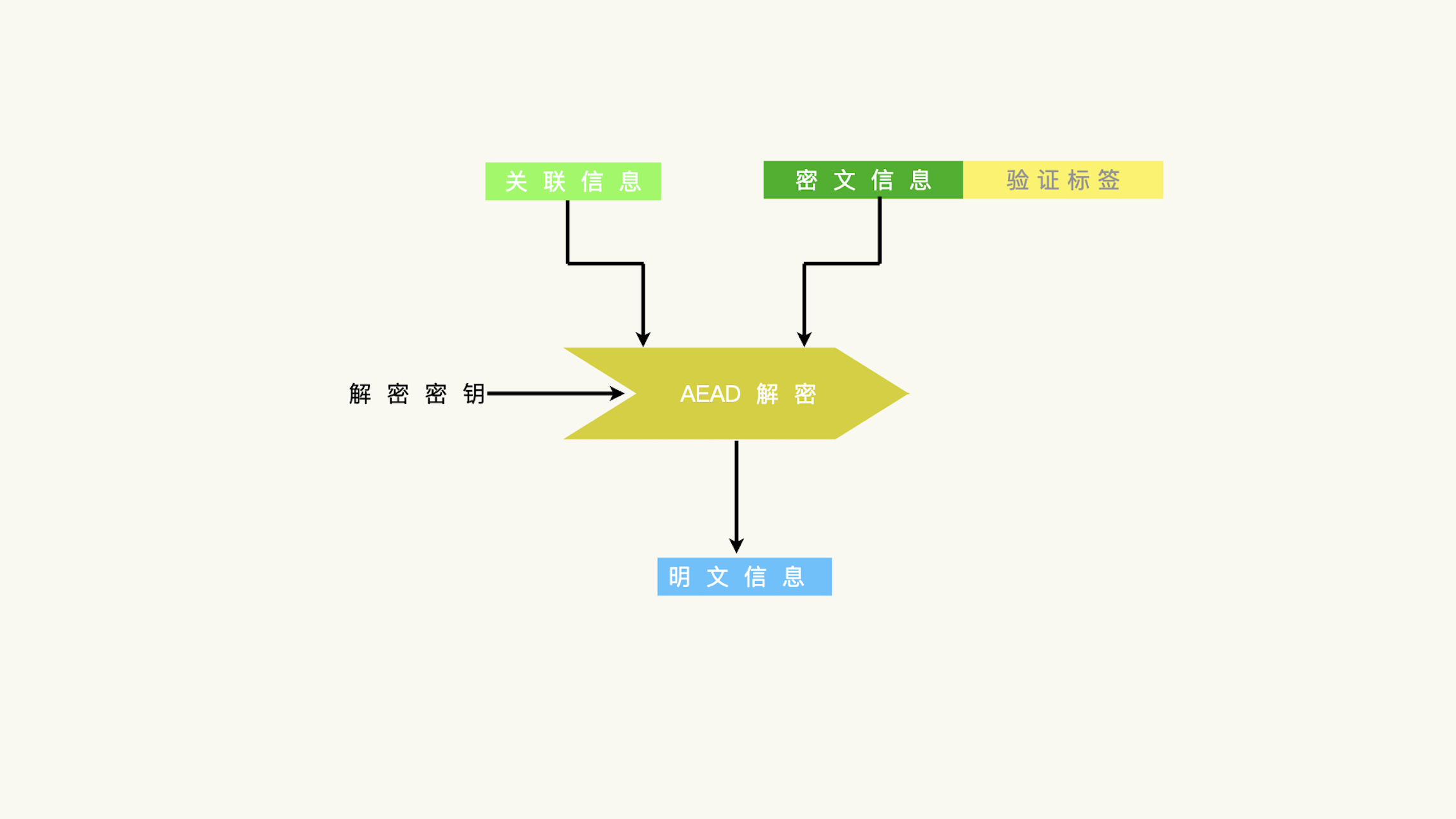
解密函数需要四个输入数据: 1.解密密钥 2.关联信息 3.密文数据 4.验证标签。输出的是明文信息,只有明文信息和关联信息的完整性都得到验证,才会有明文信息输出。¶
备注
带关联的认证加密算法的广泛使用,也使得曾经占据主导地位的 CBC 算法可以从容地退出历史舞台。因为,带关联的认证加密算法能够进行自我验证。
15 | AEAD 有哪些安全陷阱¶
加密数据要能够自我验证,自我验证就是指解密的时候,还能够同时检验数据的完整性。
带关联数据的认证加密(AEAD)是目前市场的主流思路。
有哪些常见的算法¶
常见的 AEAD 模式有三种:
1. GCM
2. CCM
3. Poly1305
可以把带关联数据的认证加密看做一个加密模式,就像 CBC 模式一样,我们可以和前面提到的 AES 等加密算法进行组合。但 ChaCha20 和 Poly1305 通常组合在一起;Camellia 与 AES 通常和 GCM 以及 CCM 组合在一起。
综合考虑加密算法和加密模式,当前推荐使用的、有广泛支持的、风险最小的算法是:
1. AES/GCM
2. ChaCha20/Poly1305
3. AES/CCM
AEAD 有风险吗¶
AEAD 算法,都需要使用初始化向量。初始化向量选择的一个原则:在一个对称密钥的生命周期里,初始化向量不能重复。所以,对于 AES/GCM 算法,同样的对称密钥,一定不要使用重复的初始化向量。否则的话,就存在安全漏洞。
备注
初始化向量的重复问题,就是使用 AEAD 算法的最大风险,也是最难处理的风险。
初始化向量-随机数¶
该怎么解决初始化向量在信息发送方和接收方之间的同步问题?这是使用随机数作为初始化向量必须要考虑清楚的问题。对于 AEAD 算法,初始化向量并不需要保密。一个常用的方案,信息发送方发送加密信息的时候,可以把明文的初始化向量一起发送。信息接收方直接使用接收到的明文初始化向量,就可以解密加密数据了。
备注
需要注意随机数的大小。对于这个问题,我们要再次考虑初始化向量选择的原则,在一个对称密钥的生命周期里,初始化向量不能重复。也就是说,随机数必须有足够的容量,使得在对称密钥的生命周期里,都不太可能出现重复的随机数。最常用的经验数据,是使用 64 位的随机数。64 位的初始化向量,支持 2^64 的加密运算。
使用随机数作为初始化向量,还有一个常被忽视的小缺陷。随机数的初始化通常是一个费时费力的过程。在应用程序里,大量的随机数实例的初始化可能会造成应用程序的性能问题,甚至包括应用程序的停顿。
初始化向量-序列数¶
备注
对于 AEAD 算法,只要初始化向量不重复就行,并不要求初始化向量不可预测。避免昂贵的随机数,是我们在使用密码学技术时,要经常考虑的问题。使用序列数作为初始化向量,就是一个最流行的方案。
使用静态的对称密钥,特别需要注意序列数的静态化。比如说,对称密钥存在磁盘上,每次启动程序,都加载该密钥。那么,如果序列数没有对应的保存下来,每次启动的应用程序就有可能使用重复的序列数,从而带来严重的安全问题。如果序列数也保存在磁盘上,并且每次程序启动时,加载密钥的时候,也加载序列数,我们也需要注意多线程的同步问题,其实也不省心。这种状况太理想了,有很强的局限性,只能在严格的、没有序列数错配的场景使用。
备注
信息发送方可以像使用随机数初始化向量一样,发送加密信息的时候,把明文的初始化向量(也就是序列数)一起发送。这一个方案,兼顾了信息发送方的效率,规避了信息接收方的顾虑,是目前最常用的初始化向量选择方案。
16 | 为什么说随机数都是骗人的¶
“人能做出两种随机数。一种是欺骗自然的,算的很快,状态域超大,统计上随机;一种是欺骗人的,通常无法预测下一个是多少,通常算的慢”。
备注
有了量子计算机就可以生成真正的随机数了。量子计算机对密码学既是打击,也是促进。
随机数怎么来的¶
备注
即便我们知道了随机数产生的机制,以及所有的已经产生的随机数,我们也无法预测下一个随机数是什么。这就是随机数的第一个特点:不可预测。
备注
只要有一个随机性统计检验方法没有通过,这个随机数产生的机制就是有问题的。换句话说,对于合格的随机数,我们没有办法验证下一个随机数随不随机。这就是随机数的第二个特点:无法证伪。
产生随机数的诀窍,就是把“相同的数据输入”拆成两部分。一部分是私密的数据,一部分是公开的数据。如果我们能保护住私密的数据,对于别人或者别的机器来说,可能就是无法预测的。这个私密数据的质量和计算输出的算法,就决定了随机数的质量。
现在几乎所有主流的计算机,都内嵌了随机数发生器;主流的操作系统或安全类库,都提供了随机数的接口。一般来说,我们不需要自行设计随机数算法,保守私密数据的秘密。
需要注意两点:
1. 第一点是,随机数的产生可能会阻塞
2. 第二点是,随机数的强度要匹配
阻塞的随机数有什么麻烦¶
随机数也是有质量要求的,为了保证随机数的质量,随机数发生器的设计需要收集随机信息,比如计算机的噪音,周围的温度,CPU 的状态,硬盘的状态,用户的行为等等。
这些信息收集,是需要时间的,所以有的时候,产生下一个随机数的时候,就会阻塞。阻塞的时间还不确定,有的可能是纳秒级别的,有的可能是秒甚至分钟级别的。而对于一个高吞吐量的系统,微秒级别的阻塞可能都是不能忍受的。
重要
除非万不得已,我们尽量不要使用阻塞的随机数发生器。
非阻塞的随机数还能随机吗¶
备注
非阻塞的随机数发生器也需要收集随机信息。区别在于随机信息怎么使用,以及使用的频率。
阻塞的随机数发生器的每一个随机数,都要损耗随机信息;而非阻塞的随机数发生器,可能仅仅在开始的时候就损耗随机信息(比如说一台计算机开机的时候),然后,随机数的发生就不再损耗随机信息了。只要不再损耗随机信息,就不会有收集随机信息带来的阻塞了。
什么是确定性的随机数发生器¶
确定性的随机数发生器(Deterministic Random Bit Generator, DRBG)
备注
确定性说的就是相同的输入,有相同的运算结果。这也就意味着,对于确定性的随机数发生器来说,它的下一个随机数是确定的,是可以计算出来的,当然也是可以预测的。
随机数发生器持有私密的数据,所以计算结果对它来说,是确定的。如果我们不知道私密的数据,从随机数发生器外面看起来,下一个随机数还是能够做到貌似不可预测的。
怎么使用哈希函数实现随机¶
使用单向散列函数实现非阻塞的随机数发生器的关键,就是把这部分私密的数据,当做单向散列函数输入的一部分,然后再加入不会重复的数据,比如序列数。
备注
使用单向散列函数和有限的随机信息,随机性能够满足“不可预测”和“无法证伪”这两个检验指标。要优先使用这些已经经过验证的、成熟的设计和实现。
随机数也有强度吗¶
对于阻塞的随机数发生器来说。随机数每一位损耗的都是计算机收集的随机信息。随机数的位数也就是它的安全强度。所以,通常的,我们不担心它的安全强度。
对于非阻塞的随机数发生器,它只损耗有限的随机信息,通过单向散列函数来计算随机数。这也就意味着两个问题:
1. 单向散列函数本身是有安全强度的。
相应的随机数发生器的安全强度,不会超过单向散列函数的安全强度。
如: SHA-256 的安全强度是 128 位
那使用它的随机数发生器的安全强度一般也不会高于 128 位
2. 单向散列函数的输出长度是固定的,而随机数的长度可能并不匹配散列值的长度
SHA-256 的散列值长度是 256 位,如果要产生一个 512 位的随机数
就需要至少两个散列值的拼接
有哪些常见的随机数算法¶
基于单向散列函数的 Hash-DRBG 和基于 HMAC 的 HMAC-DRBG。一般来说,Hash-DRBG 算法初始化的时候需要使用有限的随机信息。而对于 HMAC-DRBG 算法来说,这个有限的随机信息被保密的对称密钥取代了。
无论是随机信息还是已知的对称密钥,都是需要保密的信息。所以,使用保密的对称密钥取代随机信息,并没有安全上的妥协。
使用保密的对称密钥取代随机信息还有一个好处。一般来说,对于应用程序来说,随机信息是透明的,只有机器知道,应用程序并不知道随机信息是什么。而使用对称密钥,只要知道了对称密钥,应用程序就有复制随机数的办法。这一点,对于很多应用场景,都有着重要的意义。
17 | 加密密钥是怎么来的¶
AES-128 和 AES-256 算法中的 128 和 256,指的是密钥的长度。对称密钥的长度是由对称密钥算法确定的。
备注
对称密钥要满足的三个条件:长度、强度和秘密
对称密钥的强度¶
备注
对称密钥的强度一定要和加密算法的强度匹配。比如,AES-128 算法需要 128 位的密钥,这个密钥就要有 128 位的强度。
如果密钥只能是阿拉伯数字,那么 128 位的密钥就只有 10^16 种可能性。也就是,如果使用蛮力攻击的话,最多需要 10^16 次尝试,加密密钥就能够找到,加密数据就能够被破解。如果我们把 10^16 转换成按位表示的安全强度,也不过就是 53 位的安全强度,这离 128 位的安全强度可相差太远了。
产生密钥的机制:
1. 首先,产生密钥的机制要有匹配的强度
如果产生密钥的机制只有 128 位的安全强度,它就不能提供 256 位安全强度的密钥
2. 其次,密钥在它的长度上要均匀分布。
也就是说,这个密钥的每一位是 0 还是 1 的概率都是 50%。
如果不能做到均匀分布,就会降低密钥的安全性。
3. 密钥生成机制产生的密钥要随机。
备注
一个合格的对称密钥,它的长度和强度要与对称密钥算法相匹配。
对称密钥的秘密¶
一个合格的对称密钥,要有足够的秘密,并且它的长度和强度要与对称密钥算法相匹配。
秘密的来源,来源主要有两类:
1. 一类是计算机用户持有的秘密
2. 另一类是计算机持有的秘密
指纹、面容、虹膜等我们拥有的生物特征不可靠,我们能够记住的又太少,那为什么指纹识别和用户密码还这么流行呢?主要原因是还是没有更好的、更简单的办法。
使用口令生成对称密钥¶
备注
口令的强度不够,那如果一段加密数据,只有用户参与才能解密,那该怎么办呢?解决的办法就是分级:使用弱的口令来保护强的密钥,然后使用强的密钥来保护私密数据。
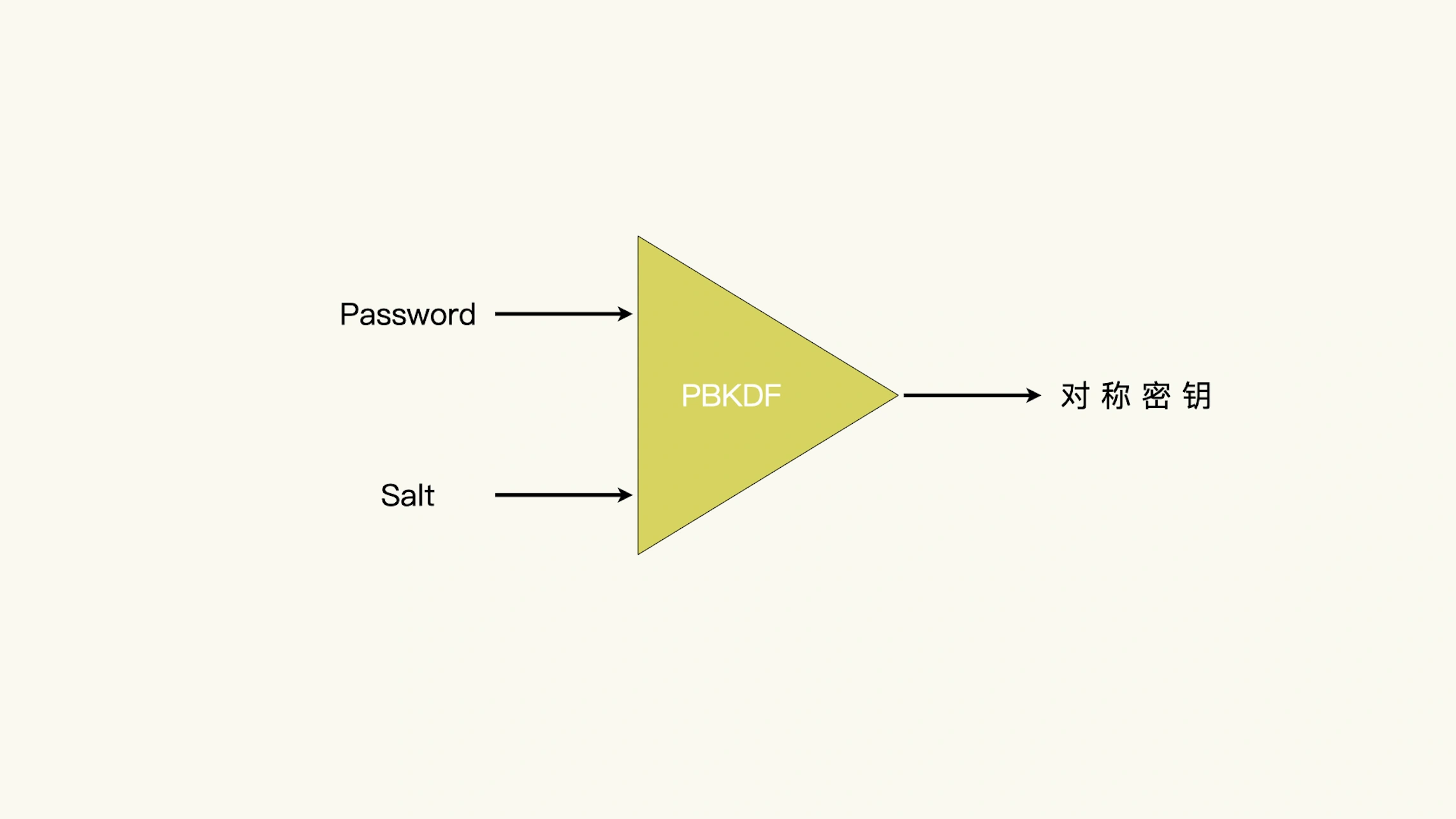
基于口令的密钥推导¶
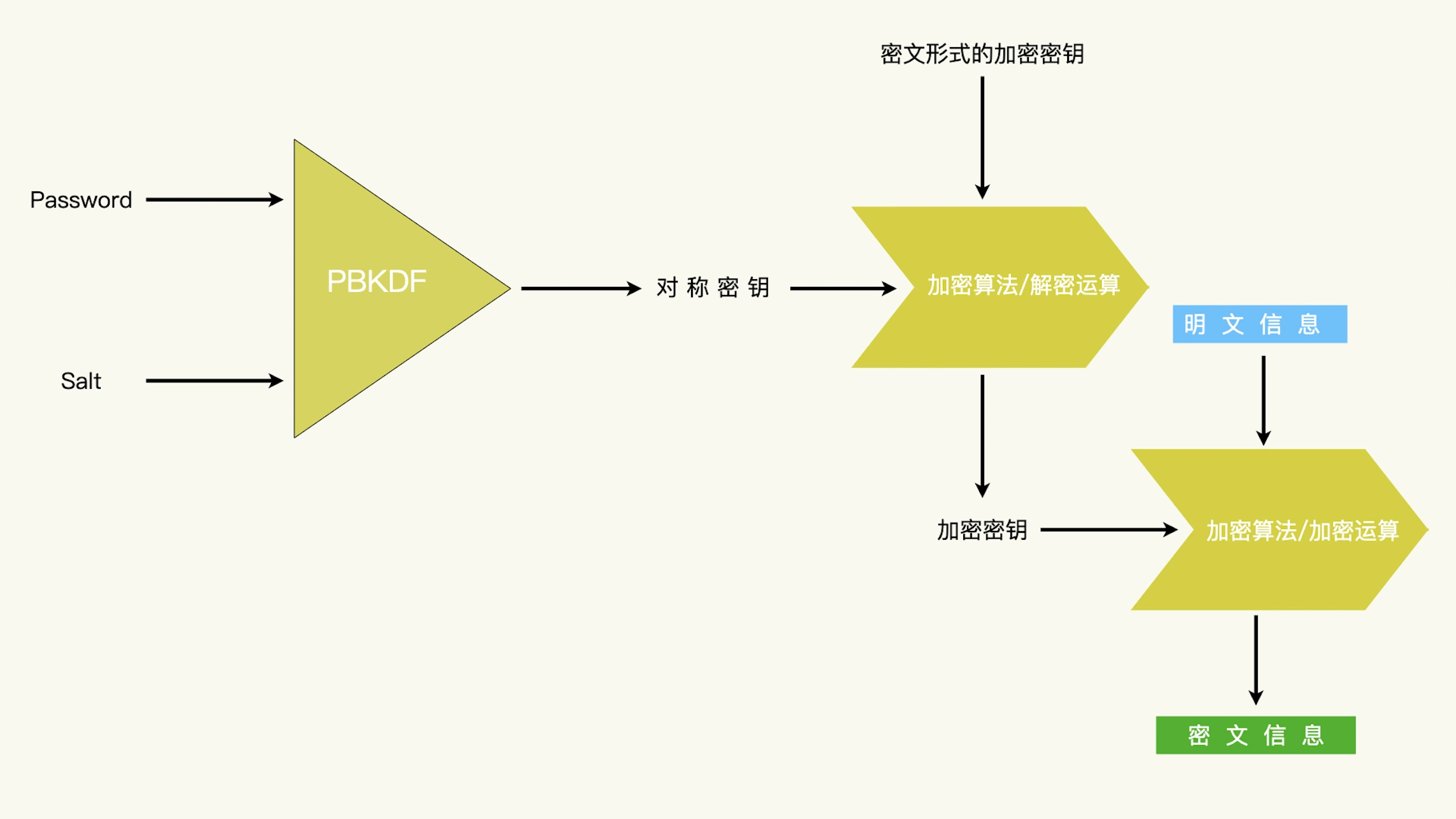
使用推导出的密钥保护一个使用时间更长的密钥;而使用时间更长的密钥用来保护私密数据。¶
18 | 如何管理对称密钥¶
即用即弃的对称密钥¶
即用即弃的对称密钥可以用在加密数据不需要保存的场景。比如说:
1. HTTPS 这样的端到端传输协议
2. 加密数据需要保存的场景
在解密的时候,用口令再生成一个完全相同的对称密钥
需要留存的对称密钥¶
备注
需要留存的对称密钥,大部分出现在用户无法参与的计算环境里。比如自动启动的服务器。在用户能够参与的计算环境里,不应该使用需要留存的对称密钥。取而代之的,应该是由用户持有的、不需要存储的秘密推导出来的即用即弃的对称密钥。
对称密钥有什么麻烦¶
如果每两人之间的通信都使用不同的密钥,那么:
3 个参与者的系统,需要 3 对不同的对称密钥。
5 个参与者的系统,需要 10 对不同的对称密钥;
10 个参与者的系统,需要 45 对不同的对称密钥;
100 个参与者的系统,需要 4950 对不同的对称密钥。
对称密钥系统:
1. 每两人之间的通信都使用不同的密钥
2. 只有一个与云服务厂商通信的密钥
3. Kerberos 协议
kerberos解决的问题是怎么通过集中认证的手段,解决对称密钥规模化分发的问题。集中认证只是手段,解决的问题是怎么在两个实体之间协商出对称密钥。
总结¶
有意识优先使用即用即弃的对称密钥;
有意识去保护好需要留存的对称密钥;
知道对称密钥在规模化通信场景下的麻烦,能够有意识地去寻找、学习相应的解决方案。
19|量子时代,你准备好了吗¶
量子算力有多强¶
2020 年 12 月 4 日,中国量子计算原型机 “九章” 问世。理论上,这个计算机比目前最快的计算机还要快一百万亿倍。也比 2019 年谷歌发布的量子计算原型机 “悬铃木” 快一百亿倍。
备注
非对称密码算法,不能抵御量子计算时代的算力。量子计算时代的非对称密码算法目前还在遴选中,而主流的密钥交换算法一般都是建立在非对称密码技术之上的。在后量子时代的非对称密码算法普及之前,抵御量子计算时代的算力的办法就是要使用具备前向保密性的对称密钥。所以,对于现在的安全协议来说,要求具备前向保密性是一个硬指标。
256 位的算法安全吗¶
“九章” 破解 128 位的安全强度,只需要 2.5% 的年,也就是大约 9 天。量子计算机的研发还在原型阶段,成熟的量子计算机,性能可能还会有大幅度的提高。到了量子计算机成熟的时候,破解 128 位的安全强度,可能只是微秒或者纳秒级别的计算。所以,量子计算时代,128 位的安全强度也就不再安全了。
假设量子计算机一纳秒就可以破解 128 位的安全强度,我们有 10 亿台这样的量子计算机破解 256 位的安全强度,要一千万个十亿年。所以,在量子计算时代,256 位的安全强度也是足够安全的。
什么是前向保密性¶
备注
在密码学里,前向保密性指的是即使用来协商或者保护数据加密密钥的长期秘密泄漏,也不会导致数据加密密钥的泄漏。静态密钥不能前向保密
关键就在于使用用完就丢、而且用完就不能再找回的秘密,比如说随机数。如果随机数也参与数据加密密钥的衍生,只要这个衍生算法是安全的,那这个数据加密密钥也就具有了随机性。只要生成这个数据加密密钥的随机数被干干净净地丢弃了,别人就不太可能重新找回这个随机数,也就不能再次推导出同样的数据加密密钥了。
具备前向保密性的对称密钥的两个特点:
1. 密钥的产生需要有即用即弃的随机数的参与
2. 密钥的本身是即用即弃的密钥,而不能是静态的密钥
结束语¶
备注
密码学本身并不难学,困难在于追踪密码学的最新进展,了解密码分析的最新动向,知道什么时候该抛弃,知道什么问题该避免。
可以创建自己的 “禁止清单” 和 “爬坑清单”,在我们要去检查我们自己的产品有没有类似的问题时,给自己的 “禁止清单” 添加新的条目,给自己的 “爬坑清单” 添加新的场景和解决办法。
有什么好的网站可以看到别人的坑呢:
来源比较零散,关注世界性的信息安全大会,以及信息安全的新闻。
https://thehackernews.com/ 可能是信息比较密集的一个网站。





