动手学深度学习(Dive into Deep Learning)¶
英文版: https://d2l.ai/
GitHub开源地址: https://github.com/d2l-ai/d2l-en
中文版: https://zh.d2l.ai/
GitHub开源地址: https://github.com/d2l-ai/d2l-zh
发布于2021年(大模型真正兴起前)
前言¶
- 第 1 部分:基础知识和预备知识。
第 1 节 是深度学习的简介。
第 2 节,我们将快速带您了解实践深度学习所需的先决条件,例如如何存储和操作数据,以及如何应用基于线性代数、微积分和概率的基本概念的各种数值运算。
第 3 节到第 5 节涵盖深度学习中最基本的概念和技术,包括回归和分类;线性模型;多层感知器;以及过度拟合和正则化。
- 第 2 部分:现代深度学习技术。
第 6 节描述了关键的计算深度学习系统的组成部分,并为我们的更复杂模型的后续实现。
第 7 条和第 8 条存在 卷积神经网络 (CNN) 是构成 大多数现代计算机视觉系统的支柱。
第 9 节和第 10 节介绍 循环神经网络 (RNN),利用顺序模型 数据中的(例如,时间)结构,通常用于自然语言处理和时间序列预测。
第 11 节,我们描述了一类相对较新的模型,基于所谓的注意力机制,它已经取代 RNN 成为大多数自然语言处理任务的主导架构。这些部分将带您快速了解深度学习从业者广泛使用的最强大、最通用的工具。
- 第 3 部分:可扩展性、效率和应用程序。
在第 12 章中,我们讨论了几种用于训练深度学习模型的常见优化算法。
在第 13 章中,我们研究了影响深度学习代码计算性能的几个关键因素。
在第 14 章中,我们将说明深度学习在计算机视觉中的主要应用。
在第 15 章和第 16 章中,我们演示了如何预训练语言表示模型并将其应用于自然语言处理任务。
Notation¶
Numerical Objects:¶
x: a scalar
x: a vector
X: a matrix
X: a general tensor
I: the identity matrix (of some given dimension), i.e., a square matrix with 1 on all diagonal entries and 0 on all off-diagonals
Set Theory¶
X: a set
Functions and Operators¶
=: an equality asserted as a definition of the symbol on the left-hand side
Calculus¶
Probability and Information Theory¶
X : a random variable
P : a probability distribution
P(X=x) : the probability assigned to the event where random variable X takes value x
E[X] : expectation of a random variable X
额外的¶
H(X) : entropy of random variable X
H(P, Q): cross-entropy from P to Q
Part 1: Basics and Preliminaries¶
1. Introduction¶
Key Components¶
Data
Model
Function that quantifies how well (or badly) the model is doing
Algorithm to adjust the model’s parameters to optimize the objective function.
特征(协变量或 输入)-----> 标签(或目标)
features (covariates or inputs) -----> label (or target)
Kinds of Machine Learning Problems¶
Supervised Learning¶
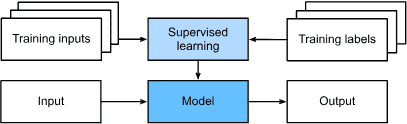
Fig. 1.3.1 Supervised learning.¶
Regression
Classification
Tagging
Search(e.g. PageRank)
Recommender Systems
- Sequence Learning
Tagging and Parsing(标记和解析): 如词性(PoS)标记, 命名实体识别
Automatic Speech Recognition(自动语音识别)
Text to Speech(文字转语音)
Machine Translation(机器翻译)

[Tagging]当分类器遇到这种图像时,我们自己就会遇到麻烦。学习预测不互斥的类的问题称为多标签分类。自动标记问题通常最好用多标签分类来描述。¶
Unsupervised and Self-Supervised Learning¶
无监督学习的进一步发展是: 自我监督学习
自我监督学习:利用某些方面的技术,使用未标记的数据提供监督。
对于文本,我们可以训练模型 通过使用它们预测随机屏蔽的单词来“填空” 大语料库中的周围单词(上下文),无需任何标记工作
对于图像,我们可以训练模型 告诉同一图像的两个裁剪区域之间的相对位置,基于图像的剩余部分来预测图像的被遮挡部分,或者预测两个示例是否是同一底层图像的变动版本。
Interacting with an Environment¶
前面的监督和无监督学习都会预先获取大量数据,然后启动模式识别机器,而无需再次与环境交互。
因为所有的学习都是在算法与环境断开连接之后进行的,所以这有时被称为离线学习
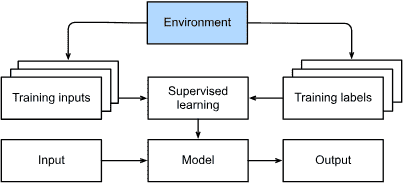
Fig. 1.3.6 Collecting data for supervised learning from an environment.¶
Reinforcement Learning¶
强化学习给出了一个非常笼统的问题描述,其中代理通过一系列时间步骤与环境进行交互。在每个时间步,代理都会从环境中接收一些观察结果,并且必须选择随后传输的操作 通过某种机制(有时称为 执行器),当每次循环之后,代理收到来自环境的奖励。然后,代理接收后续观察,并选择后续操作,依此类推。强化学习代理的行为受策略控制。简而言之,一个 政策只是将环境观察映射到行动的函数。强化学习的目标是产生好的政策。
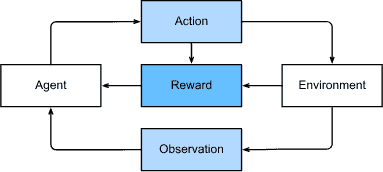
强化学习框架的通用性怎么强调都不为过。一般的强化学习问题有一个非常通用的设置。行动会影响随后的观察。仅当奖励与所选操作相对应时才会观察到奖励。
当环境被充分观察时,我们将强化学习问题称为``马尔可夫决策过程(Markov decision process)``
当状态不依赖于先前的动作时,我们将其称为
上下文强盗问题(contextual bandit problem)当没有状态,只有一组初始奖励未知的可用动作时,我们就会遇到经典的
多臂老虎机问题(multi-armed bandit problem)
Roots¶
对于一系列不同的机器学习问题,深度学习 学习为他们的解决方案提供了强大的工具。虽然很多深 学习方法是最近的发明,学习背后的核心思想 几个世纪以来,人们一直在研究数据。事实上,人类已经掌握了 渴望分析数据并预测未来的结果,并且它 这种愿望是许多自然科学的根源 数学。两个例子是伯努利分布,以 雅各布·伯努利(Jacob Bernoulli,1655-1705) ,以及卡尔·弗里德里希·高斯(Carl Friedrich Gauss,1777-1855)发现的高斯分布。
随着数据的可用性和收集,统计数据真正起飞。它的先驱之一罗纳德·费希尔(Ronald Fisher,1890-1962)对其理论及其在遗传学中的应用做出了重大贡献。他的许多算法(例如线性判别分析)和概念(例如费舍尔信息矩阵)仍然在现代统计学的基础中占有重要地位。Fisher 于 1936 年发布的 Iris 数据集有时仍用于演示机器学习算法。
对机器学习的其他影响来自克劳德·香农(1916-2001)的信息论和艾伦·图灵(1912-1954)提出的计算理论。
进一步的影响来自神经科学和心理学。毕竟, 人类明显表现出智能行为。很多学者都问过 是否可以解释并可能对这种能力进行逆向工程。 第一个受生物学启发的算法是由 唐纳德·赫布 (1904–1985) 。在他的开创性著作《行为的组织》( Hebb,1949 )中,他假设神经元通过正强化进行学习。这被称为赫布学习规则。这些想法启发了后来的工作,例如罗森布拉特的感知器学习算法,并为当今深度学习的许多随机梯度下降算法奠定了基础:强化期望的行为并减少不良行为,以获得神经网络中参数的良好设置。
神经网络的名字来源于生物学灵感。一个多世纪以来(可以追溯到 1873 年 Alexander Bain 和 1890 年 James Sherrington 的模型),研究人员一直试图组装类似于相互作用神经元网络的计算电路。
The Road to Deep Learning¶
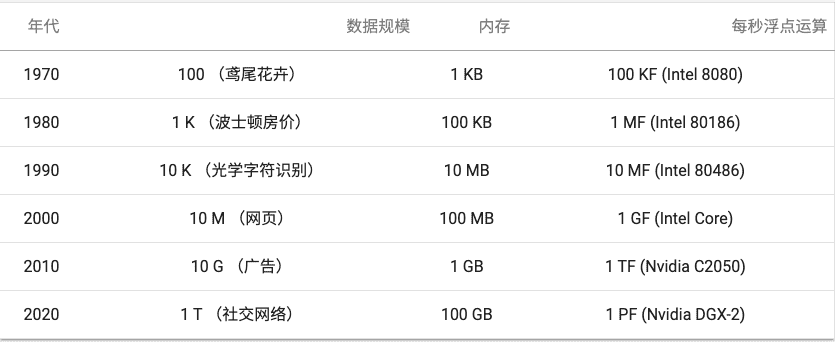
表1.5.1 数据集vs计算机内存和计算能力¶
机器学习和统计的最佳结合点 从(广义)线性模型和核方法转向深度神经网络 网络。这也是很多中流砥柱的原因之一 深度学习,例如多层感知器 ( McCulloch 和 Pitts,1943 ) ,卷积神经网络 ( LeCun等,1998 ) ,长短期记忆 ( Hochreiter 和 Schmidhuber,1997 )和 Q-Learning ( Watkins 和 Dayan,1992 )
- 下面列举了帮助研究人员在过去十年中取得巨大进步的想法
新的容量控制方法,如dropout (Srivastava et al., 2014),有助于减轻过拟合的危险。这是通过在整个神经网络中应用噪声注入 (Bishop, 1995) 来实现的,出于训练目的,用随机变量来代替权重。
注意力机制解决了困扰统计学一个多世纪的问题:如何在不增加可学习参数的情况下增加系统的记忆和复杂性。
多阶段设计。例如,存储器网络 (Sukhbaatar et al., 2015) 和神经编程器-解释器 (Reed and De Freitas, 2015)。它们允许统计建模者描述用于推理的迭代方法。
生成对抗网络 (Goodfellow et al., 2014) 。传统模型中,密度估计和生成模型的统计方法侧重于找到合适的概率分布(通常是近似的)和抽样算法。因此,这些算法在很大程度上受到统计模型固有灵活性的限制。生成式对抗性网络的关键创新是用具有可微参数的任意算法代替采样器。然后对这些数据进行调整,使得鉴别器(实际上是一个双样本测试)不能区分假数据和真实数据。通过使用任意算法生成数据的能力,它为各种技术打开了密度估计的大门。
2. Preliminaries¶
survival skills:
1) techniques for storing and manipulating data;
2) libraries for ingesting and preprocessing data from a variety of sources;
3) knowledge of the basic linear algebraic operations that we apply to high-dimensional data elements;
4) just enough calculus to determine which direction to adjust each parameter in order to decrease the loss function;
5) the ability to automatically compute derivatives so that you can forget much of the calculus you just learned;
6) some basic fluency in probability, our primary language for reasoning under uncertainty; and
7) some aptitude for finding answers in the official documentation when you get stuck.
2.1 Data Manipulation¶
广播机制
索引和切片
转换为其他Python对象:
X = torch.tensor([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]]) A = X.numpy() B = torch.tensor(A) type(A), type(B) # (numpy.ndarray, torch.Tensor) # 将大小为1的张量转换为Python标量 a = torch.tensor([3.5]) a, a.item(), float(a), int(a) # (array([3.5]), 3.5, 3.5, 3)
2.2. Data Preprocessing¶
读取数据集
处理缺失值
转换为张量格式:
import torch X = torch.tensor(inputs.to_numpy(dtype=float)) y = torch.tensor(outputs.to_numpy(dtype=float)) X, y
2.3. Linear Algebra(线性代数)¶
Scalars(标量)
Vectors(向量)
Matrices(矩阵)
Tensors(张量)
Hadamard product¶
The elementwise product of two matrices is called their Hadamard product (denoted
two matrices
A = torch.arange(6, dtype=torch.float32).reshape(2, 3)
B = A.clone() # Assign a copy of A to B by allocating new memory
A * B
tensor([[ 0., 1., 4.],
[ 9., 16., 25.]])
点积(Dot Product)¶
x = torch.arange(3, dtype=torch.float32)
y = torch.ones(3, dtype = torch.float32)
x, y
# (tensor([0., 1., 2.]), tensor([1., 1., 1.]))
torch.dot(x, y), torch.sum(x * y)
# (tensor(3.), tensor(3.))
# 过程:
# 0*1 + 1*1 + 2*1 = 3
矩阵-向量积(Matrix–Vector Products)¶
where each
The matrix-vector product
A = torch.arange(6).reshape(2, 3)
# tensor([[0, 1, 2],
# [3, 4, 5]])
x = torch.arange(3)
# tensor([0, 1, 2])
A.shape, x.shape
# (torch.Size([2, 3]), torch.Size([3])
torch.mv(A, x), A@x
# tensor([ 5., 14.]), tensor([ 5., 14.]))
# 过程:
# torch.dot([0, 1, 2], [0, 1, 2]) = 0*0+1*1+2*2=5
# torch.dot([3, 4, 5], [0, 1, 2]) = 0*3+1*4+2*5=14
矩阵-矩阵乘法(Matrix–Matrix Multiplication)¶
Say that we have two matrices
Let
To form the matrix product
我们可以将矩阵-矩阵乘法 AB 看作简单地执行 m 次矩阵-向量积,并将结果拼接在一起,形成一个 n*m 矩阵。
在下面的代码中,我们在A和B上执行矩阵乘法。 这里的A是一个5行4列的矩阵,B是一个4行3列的矩阵。 两者相乘后,我们得到了一个5行3列的矩阵。
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]])
B = torch.ones(4, 3)
tensor([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])
torch.mm(A, B)
# 输出
tensor([[ 6., 6., 6.],
[22., 22., 22.],
[38., 38., 38.],
[54., 54., 54.],
[70., 70., 70.]])
备注
矩阵-矩阵乘法(matrix–matrix multiplication) 可以简单地称为 矩阵乘法(matrix multiplication) ,不应与 Hadamard积(Hadamard product) 混淆。
2.4. Calculus(微积分)¶
逼近法就是积分(integral calculus)的起源¶
微分(differential calculus)被发明出来。 在微分学最重要的应用是优化问题,即考虑如何把事情做到最好
将拟合模型的任务分解为两个关键问题:
1. 优化(optimization): 用模型拟合观测数据的过程
2. 泛化(generalization): 数学原理和实践者的智慧,能够指导我们生成出有效性超出用于训练的数据集本身的模型
Derivatives and Differentiation(导数和微分)¶
Put simply, a
derivativeis the rate of change in a function with respect to changes in its arguments. Derivatives can tell us how rapidly a loss function would increase or decrease were we to increase or decrease each parameter by an infinitesimally small amount.简而言之,对于每个参数, 如果我们把这个参数增加或减少一个无穷小的量,可以知道损失会以多快的速度增加或减少
假设我们有一个函数
如果
f在a处是可微(differentiable)的如果
f在一个区间内的每个数上都是可微的,则此函数在此区间中是可微的可以将上面公式中的导数
f(x)相对于x的瞬时(instantaneous)变化率所谓的瞬时变化率是基于
x中的变化h,且h接近0导数的几个等价符号:
其中符号
( C 是一个常数)
(幂律(power rule), n 是任意实数)
为了微分一个由一些常见函数组成的函数, 下面的一些法则方便使用。假设函数
f和g都是可微的,C是一个常数, 则:常数相乘法则
加法法则
乘法法则
除法法则
现在我们可以应用上述几个法则来计算
令 x=1 , 我们有
当 x=1 时, 此导数也是曲线 u=f(x) 切线的斜率。
Partial Derivatives(偏导数)¶
在深度学习中,函数通常依赖于许多变量。 因此,我们需要将微分的思想推广到多元函数(multivariate function)上
设
为了计算
Gradients(梯度)¶
我们可以连结一个多元函数对其所有变量的偏导数, 以得到该函数的梯度(gradient)向量。
具体而言,设函数
函数
其中
- 假设 x 为 n 维向量, 在微分多元函数时经常使用以下规则:
对于所有
对于所有
对于所有
同样,对于任何矩阵
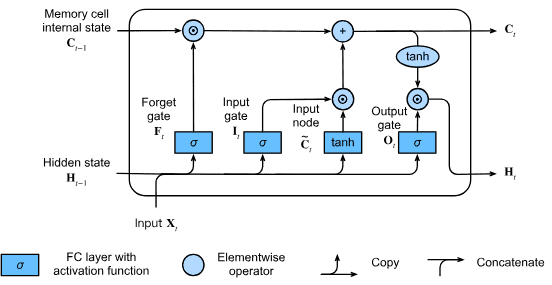
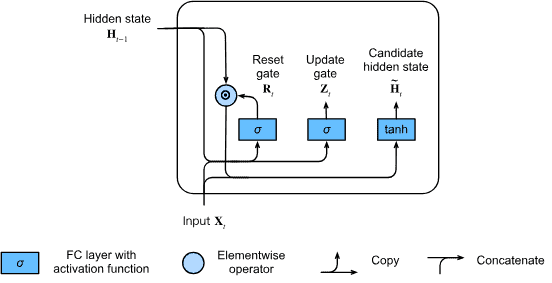
2.5. Automatic Differentiation(自动微分)¶
深度学习框架通过自动计算导数,即自动微分(automatic differentiation)来加快求导。 实际中,根据设计好的模型,系统会构建一个计算图(computational graph), 来跟踪计算是哪些数据通过哪些操作组合起来产生输出。 自动微分使系统能够随后反向传播梯度。 这里,反向传播(backpropagate)意味着跟踪整个计算图,填充关于每个参数的偏导数。
备注
grad can be implicitly created only for scalar outputs 梯度默认给标量输出创建,就是说 y 应该是个标量
import torch
x = torch.arange(4.0) # tensor([0., 1., 2., 3.])
x.requires_grad_(True) # 等价于x=torch.arange(4.0,requires_grad=True)
print(f"====1: {x.grad}") # None
y = 2 * torch.dot(x, x)
print(f"====2: y:{y}") # tensor(28., grad_fn=<MulBackward0>)
y.backward()
print(f"====3: x.grad:{x.grad}") # tensor([ 0., 4., 8., 12.])
# 在默认情况下,PyTorch会累积梯度,我们需要清除之前的值
x.grad.zero_()
y = x.sum() # grad can be implicitly created only for scalar outputs
y.backward()
x.grad # tensor([1., 1., 1., 1.])
Backward for Non-Scalar Variables¶
- 在数学中,当 𝑦 是一个向量,𝑥 也是一个向量时,𝑦 对 𝑥 的导数是一个 Jacobian 矩阵。
Jacobian 矩阵的每个元素表示 𝑦 的每个分量对 𝑥 的每个分量的偏导数。
如果 𝑦 和 𝑥 的维度都很高,求导的结果会是一个更高阶的张量。
但在深度学习中,我们通常不需要直接计算 Jacobian 矩阵,而是希望将结果进行汇总,最终得到一个和 𝑥 形状相同的向量(即梯度)
PyTorch 的处理方式:
如果对 非标量张量直接调用 .backward(),会报错。
RuntimeError: grad can be implicitly created only for scalar outputs
因为框架无法自动决定如何将非标量处理成标量。
我们需要提供一个向量(通常称为 gradient 参数),来告诉 PyTorch如何汇总梯度
y = x * x # 假设 y 是一个向量
y.backward(gradient=torch.ones(len(y)))
实际上更快的方式是直接对 𝑦 求和后再调用 .backward()
y.sum().backward()
示例:
>>> x
tensor([0., 1., 2., 3.], requires_grad=True)
>>> x.grad.zero_()
>>> y = x * x
>>> y.sum().backward()
>>> x.grad
tensor([0., 2., 4., 6.])
# 说明
# y = x1*x1 + x2*x2 + ... + xi*xi
# 导数: [2x1, 2x2, ..., 2xi]
# 即: [0, 2, 4, 6]
>>> x.grad.zero_()
>>> y = x * x
>>> y.mean().backward()
>>> x.grad
tensor([0.0000, 0.5000, 1.0000, 1.5000])
# 说明
# y = 1/i(x1*x1 + x2*x2 + ... + xi*xi)
# 导数: 1/i([2x1, 2x2, ..., 2xi])
# 即: 1/4([0, 2, 4, 6])
# [0.0000, 0.5000, 1.0000, 1.5000]
Detaching Computation¶
有时,我们希望将某些计算移动到记录的计算图之外。
例如,假设y是作为x的函数计算的,而z则是作为y和x的函数计算的。
想计算z关于x的梯度,但由于某种原因,希望将y视为一个常数, 并且只考虑到x在y被计算后发挥的作用。
x=torch.arange(4.0,requires_grad=True)
x
# tensor([0., 1., 2., 3.], requires_grad=True)
# 梯度计算分离y
y = x * x
u = y.detach()
z = u * x
z.sum().backward()
x.grad
# tensor([0., 1., 4., 9.])
# 梯度计算不分离y
x.grad.zero_()
z=y * x
z.sum().backward()
x.grad
# tensor([ 0., 3., 12., 27.])
Gradients and Python Control Flow¶
使用自动微分的一个好处是: 即使构建函数的计算图需要通过Python控制流(例如,条件、循环或任意函数调用),我们仍然可以计算得到的变量的梯度
示例-while循环的迭代次数和if语句的结果都取决于输入a的值:
def f(a): b = a * 2 while b.norm() < 1000: b = b * 2 if b.sum() > 0: c = b else: c = 100 * b return c
计算梯度:
a = torch.randn(size=(), requires_grad=True) # tensor(0.0412, requires_grad=True)
d = f(a) # tensor(1350.7505, grad_fn=<MulBackward0>)
d.backward()
a.grad
# tensor(32768.)
a.grad == d / a # 不管怎么算,对a的梯度就是除a外的常数,因为f(a)=常数*a
# tensor(True)
2.6 Probability and Statistics¶
基本概率论¶
在统计学中,我们把从概率分布中抽取样本的过程称为抽样(sampling)
概率论公理¶
在处理骰子掷出示例时,我们将集合
S={1,2,3,4,5,6}称为 样本空间(sample space)或结果空间(outcome space) , 其中每个元素都是结果(outcome)。事件(event) 是一组给定样本空间的随机结果。 例如,“看到5”(
{5})和“看到奇数”({1,3,5})都是掷出骰子的有效事件。 注意,如果一个随机实验的结果在- 概率(probability) 可以被认为是将集合映射到真实值的函数。在给定的样本空间
对于任意事件
整个样本空间的概率为 1 , 即
对于互斥(mutually exclusive)事件(对于所有
- 概率(probability) 可以被认为是将集合映射到真实值的函数。在给定的样本空间
上面这个就是概率论的公理,由科尔莫戈罗夫于1933年提出
随机变量¶
随机变量(random variable)
为了简化符号
一方面,我们可以将
P(X)表示为随机变量X上的分布(distribution): 分布告诉我们X获得某一值的概率;另一方面,我们可以简单用P(a)表示随机变量取值 a 的概率一方面,我们可以将
P(1<=X<=3)表示事件{1<=X<=3}的概率;另一方面,P(1<=X<=3)表示随机变量X从 {1,2,3} 中取值的概率注意:离散(discrete)随机变量(如骰子的每一面) 和连续(continuous)随机变量(如人的体重和身高)之间存在微妙的区别
处理多个随机变量¶
联合概率¶
联合概率(joint probability)
P(A=a, B=b): 给定任意值 a 和 b , 联合概率可以回答: A=a 和 B=b 同时满足的概率是多少?请注意, 对于任何 a 和 b 的取值,
A=a 和 B=b,A=a就必须发生
条件概率¶
联合概率的不等式带给我们一个有趣的比率:
我们称这个比率为条件概率(conditional probability), 并用
A=b前提下B=b的概率。
贝叶斯定理¶
使用条件概率的定义,我们可以得出统计学中最有用的方程之一: 贝叶斯定理(Bayes’ theorem)
根据 乘法法则(multiplication rule) 可得到
根据对称性, 可得到
P(B)>0, 求解其中一个条件变量, 我们得到
P(A, B) 是一个联合分布(joint distribution)
P(A mid B) 是一个条件分布(conditional distribution)
边际化¶
边际化(marginalization):为了能进行事件概率求和, 我们需要
求和法则 (sum rule), 即 B 的概率相当于计算 A 的所有可能选择, 并将所有选择的联合概率聚合在一起:
边际化结果的概率或分布称为边际概率(marginal probability) 或边际分布(marginal distribution)。
独立性¶
另一个有用属性是依赖(dependence)与独立(independence)。
如果两个随机变量 A 和 B 是独立的,意味着事件 A 的发生跟 B 事件的发生无关。在这种情况下,统计学家通常将这一点表述为
根据贝叶斯定理,马上就能同样得到
在所有其他情况下,我们称 A 和 B 依赖。
比如,两次连续抛出一个骰子的事件是相互独立的。相比之下,灯开关的位置和房间的亮度并不是(因为可能存在灯泡坏掉、电源故障,或者开关故障)
如果 A 和 B 是独立的,则
同样地, 给定另一个随机变量 C 时, 两个随机变量 A 和 B 是条件独立的(conditionally independent),有
这个情况表示为
应用示例¶
条件概率 |
H=1 |
H=0 |
|---|---|---|
1 |
0.01 |
|
0 |
0.99 |
如果
运用边际化和乘法法则来确定
于是
第2次的测试概率
条件概率 |
H=1 |
H=0 |
|---|---|---|
0.98 |
0.03 |
|
0.02 |
0.97 |
现在我们可以应用边际化和乘法规则:
最后,鉴于存在两次阳性检测,患者患有艾滋病的概率为
期望和方差¶
- 假设某项投资有:
50% 的概率会失败
40% 的概率它可能提供 2倍回报
10% 的概率它可能会提供 10 倍回报 。
计算预期回报,我们总结了所有回报,将每个回报乘以它们发生的概率。
期望=
0.5*0 + 0.4*2 + 0.1*10因此 预期回报率为1.8
一个随机变量 X 的 期望(expectation)/平均值(average) 表示为
当函数
f(x)的输入是从分布P中抽取的随机变量时,f(x)的期望值为
一个随机变量 X 的 密度
在许多情况下,我们希望衡量随机变量 X 与其期望值的偏置。这可以通过方差来量化
方差的平方根被称为 标准差(standard deviation)
随机变量函数的方差衡量的是:当从该随机变量分布中采样不同值 x 时,
函数值偏离该函数的期望的程度:
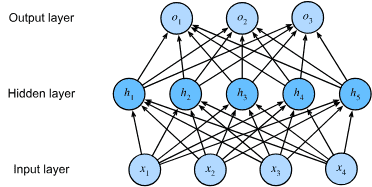
3. Linear Neural Networks for Regression¶
3.1. Linear Regression¶
Basics¶
Model¶
在机器学习中,我们通常使用高维数据集,在这种情况下使用紧凑的线性代数表示法会更方便
当我们的输入由 d 特征组成时,我们可以为每个特征分配一个索引(在 1 和 d 之间)并表达我们的预测
将所有 特征 收集到向量
通过设计矩阵
Loss Function¶
损失函数量化目标的实际值和预测值之间的距离。损失通常是一个非负数,其中值越小越好,完美的预测会导致损失为 0。
对于回归问题,最常见的损失函数是平方误差。
对示例 i 的预测为
注意,由于其二次方形式,估计
训练模型时, 我们寻求能够最小化所有训练示例的总损失的参数
Analytic Solution(解析解)¶
线性回归的解可以用一个公式简单地表达出来, 这类解叫作解析解(analytical solution)。
线性回归的目标是找到一组参数 w 和偏置 b,使得预测值与真实值之间的误差最小化。为了简化问题,可以将偏置项 b 合并到参数向量 w 中,方法是在设计矩阵 X 的每一行末尾添加一个1,从而将偏置视为权重的一部分。
备注
像线性回归这样的简单问题存在解析解,但并不是所有的问题都存在解析解。 解析解可以进行很好的数学分析,但解析解对问题的限制很严格,导致它无法广泛应用在深度学习里。
Minibatch Stochastic Gradient Descent¶
梯度下降(gradient descent):它通过不断地在损失函数递减的方向上更新参数来降低误差。梯度下降最简单的用法是计算损失函数(数据集中所有样本的损失均值) 关于模型参数的导数(在这里也可以称为梯度)
小批量随机梯度下降(minibatch stochastic gradient descent):在每次需要计算更新的时候随机抽取一小批样本的梯度下降。使用小批量随机梯度下降是因为梯度下降在实际中的执行可能会非常慢:原因是在每一次更新参数之前,我们必须遍历整个数据集。
在每次迭代中,我们首先随机抽样一个小批量
我们用下面的数学公式来表示这一更新过程(
总结一下,算法的步骤如下:(1)初始化模型参数的值,如随机初始化;(2)从数据集中随机抽取小批量样本且在负梯度的方向上更新参数,并不断迭代这一步骤。对于平方损失和仿射变换,我们可以明确地写成如下形式:
备注
更艰巨的任务是找到能够对以前未见过的数据进行准确预测的参数,这一挑战称为泛化。The more formidable task is to find parameters that lead to accurate predictions on previously unseen data, a challenge called generalization.
Predictions(预测)¶
给定模型
Vectorization for Speed¶
使用torch向量库比直接使用for循环要快3个数量级
The Normal Distribution and Squared Loss¶
正态分布的公式
其中:
μ:均值(mean),表示分布的中心。
𝜎^2 :方差(variance),表示分布的宽度,反映数据的离散程度
𝜎 越大,分布越宽、越平
𝜎 越小,分布越窄、越尖
Linear Regression as a Neural Network¶
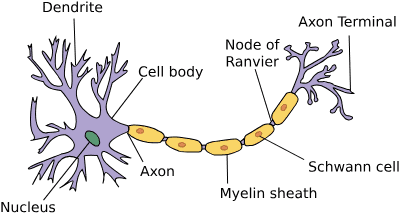
由树突(dendrites,输入终端)、 细胞核(nucleus,CPU)组成的生物神经元图片。 轴突(axon,输出线)和轴突端子(axon terminal,输出端子) 通过突触(synapse)与其他神经元连接。consisting of dendrites (input terminals), the nucleus (CPU), the axon (output wire), and the axon terminals (output terminals), enabling connections to other neurons via synapses.¶
备注
过程:来自其他神经元(或环境传感器)的信息
3.2. Object-Oriented Design for Implementation¶
实现了几个对象类:
HyperParameters
ProgressBoard
Module
DataModule
Trainer
3.3. Synthetic Regression Data¶
分别介绍了使用 生成数据集 和 读取数据集
还介绍了使用
torch.utils.data.TensorDataset和torch.utils.data.DataLoader的简洁实现实现数据加载器对象类:
SyntheticRegressionData
3.4. Linear Regression Implementation from Scratch¶
从头开始实现整个方法,包括(i)模型; (ii) 损失函数; (iii) 小批量随机梯度下降优化器; (iv) 将所有这些部分拼接在一起的训练函数。
3.4.1. Defining the Model¶
# 从平均值为 0、标准差为 0.01 的正态分布中抽取随机数来初始化权重
# 魔法数字 0.01 在实践中通常效果很好
class LinearRegressionScratch(d2l.Module): #@save
"""The linear regression model implemented from scratch."""
def __init__(self, num_inputs, lr, sigma=0.01):
super().__init__()
self.save_hyperparameters()
self.w = torch.normal(0, sigma, (num_inputs, 1), requires_grad=True)
self.b = torch.zeros(1, requires_grad=True)
# 生成的 forward 方法
def forward(self, X):
return torch.matmul(X, self.w) + self.b
3.4.2. Defining the Loss Function¶
返回小批量中所有示例的平均损失值(使用平方损失函数):
@d2l.add_to_class(LinearRegressionScratch) #@save
def loss(self, y_hat, y):
l = (y_hat - y) ** 2 / 2
return l.mean()
3.4.3. Defining the Optimization Algorithm¶
SGD(随机梯度下降) 优化器:
class SGD(d2l.HyperParameters): #@save
"""Minibatch stochastic gradient descent."""
def __init__(self, params, lr):
self.save_hyperparameters()
def step(self):
for param in self.params:
param -= self.lr * param.grad
def zero_grad(self):
for param in self.params:
if param.grad is not None:
param.grad.zero_()
定义 configure_optimizers 方法,它返回 SGD 类的实例:
@d2l.add_to_class(LinearRegressionScratch) #@save
def configure_optimizers(self):
return SGD([self.w, self.b], self.lr)
3.4.4. Training¶
- 执行以下循环(小批量随机梯度下降)
Initialize parameters
- Repeat until done
Compute gradient
Update parameters
在每个 epoch 传递一次验证数据加载器来测量模型性能
@d2l.add_to_class(d2l.Trainer) #@save
def prepare_batch(self, batch):
return batch
@d2l.add_to_class(d2l.Trainer) #@save
def fit_epoch(self):
self.model.train()
for batch in self.train_dataloader:
loss = self.model.training_step(self.prepare_batch(batch))
self.optim.zero_grad()
with torch.no_grad():
loss.backward()
if self.gradient_clip_val > 0: # To be discussed later
self.clip_gradients(self.gradient_clip_val, self.model)
self.optim.step()
self.train_batch_idx += 1
if self.val_dataloader is None:
return
self.model.eval()
for batch in self.val_dataloader:
with torch.no_grad():
self.model.validation_step(self.prepare_batch(batch))
self.val_batch_idx += 1
使用学习率 lr=0.03 训练模型并设置 max_epochs=3
model = LinearRegressionScratch(2, lr=0.03)
data = d2l.SyntheticRegressionData(w=torch.tensor([2, -3.4]), b=4.2)
trainer = d2l.Trainer(max_epochs=3)
trainer.fit(model, data)
with torch.no_grad():
print(f'error in estimating w: {data.w - model.w.reshape(data.w.shape)}')
print(f'error in estimating b: {data.b - model.b}')
# error in estimating w: tensor([ 0.1408, -0.1493])
# error in estimating b: tensor([0.2130])
3.5. Concise Implementation of Linear Regression¶
3.5.1. Defining the Model¶
class LinearRegression(d2l.Module): #@save
"""The linear regression model implemented with high-level APIs."""
def __init__(self, lr):
super().__init__()
self.save_hyperparameters()
self.net = nn.LazyLinear(1)
self.net.weight.data.normal_(0, 0.01)
self.net.bias.data.fill_(0)
3.5.2. Defining the Loss Function¶
@d2l.add_to_class(LinearRegression) #@save
def loss(self, y_hat, y):
fn = nn.MSELoss()
return fn(y_hat, y)
3.5.3. Defining the Optimization Algorithm¶
@d2l.add_to_class(LinearRegression) #@save
def configure_optimizers(self):
return torch.optim.SGD(self.parameters(), self.lr)
3.5.4. Training¶
model = LinearRegression(lr=0.03)
data = d2l.SyntheticRegressionData(w=torch.tensor([2, -3.4]), b=4.2)
trainer = d2l.Trainer(max_epochs=3)
trainer.fit(model, data)
估计参数与其真实的对应参数的对比
@d2l.add_to_class(LinearRegression) #@save
def get_w_b(self):
return (self.net.weight.data, self.net.bias.data)
w, b = model.get_w_b()
print(f'error in estimating w: {data.w - w.reshape(data.w.shape)}')
print(f'error in estimating b: {data.b - b}')
3.6. Generalization¶
3.6.1. Training Error and Generalization Error¶
训练误差表示为总和(训练数据集上计算的统计量)
训练误差是在训练集上计算的误差,是一个统计量。
它反映模型在训练集上的拟合程度。
泛化误差则表示为积分(integral)
泛化误差是在真实分布上的误差,是一个期望。
泛化误差是对无限多数据样本的期望。
泛化误差是对基础分布的预期: 可以将泛化错误视为如果您将模型应用于从同一基础数据分布中提取的无限附加数据示例流
有问题的是,我们永远无法准确计算泛化误差
真实数据分布
无法获取无限数据,只能在有限的训练集和测试集上进行评估。
因此,泛化误差只能通过测试集近似估计,而非精确计算。
在实践中,我们必须通过将我们的模型应用到一个独立的测试集来估计泛化误差,该测试集由随机选择的示例
备注
请注意,我们最终得到的模型明确取决于训练集的选择,因此训练误差通常是对基础总体真实误差的有偏估计。泛化的核心问题是我们什么时候应该期望我们的训练误差接近总体误差(以及泛化误差)。
备注
【总结】训练误差是对训练数据的拟合程度,而泛化误差反映模型在真实分布上的表现。泛化误差无法直接计算,但可以通过测试集估计。泛化的核心问题是如何使训练误差与泛化误差尽可能接近,从而确保模型在新数据上的表现良好。
3.6.2. Underfitting or Overfitting?¶
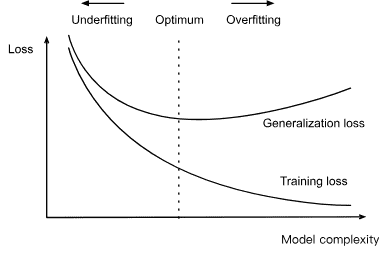
Fig. 3.6.1 Influence of model complexity on underfitting and overfitting.¶¶
3.6.3. Model Selection¶
通常,我们只有在评估了多个不同方面(不同的架构、训练目标、选定的特征、数据预处理、学习率等)的模型后才选择最终模型。在众多模型中进行选择被恰当地称为模型选择。
【Cross-Validation】当训练数据稀缺时,我们甚至可能无法提供足够的数据来构成适当的验证集。此问题的一种流行解决方案是采用 K 折叠交叉验证。这里,原始训练数据被分成 K 个不重叠的子集。然后执行模型训练和验证 K 次,每次对 K-1 子集进行训练并在不同的子集(该轮中未用于训练的子集)上进行验证。最后,通过对 K 实验结果进行平均来估计训练和验证误差。
3.6.4. Summary¶
- 经验法则
使用验证集(或 K-折叠交叉验证, k-fold cross-validation)进行模型选择;
更复杂的模型通常需要更多的数据;
复杂性的相关概念包括参数的数量和它们允许采用的值的范围;
在其他条件相同的情况下,更多的数据几乎总是能带来更好的概括;
在讨论模型的泛化能力时,通常假设训练数据和测试数据是独立同分布(IID)的。如果放宽这一假设,允许训练和测试期间的数据分布发生变化(即分布漂移),那么在没有其他(可能更弱的)假设的情况下,我们无法对模型的泛化能力做出任何保证。
独立同分布(IID)假设:是许多统计学习理论的基础。它假定训练数据和测试数据来自相同的分布,且各个样本之间相互独立。
在这种假设下,可以推导出模型在新数据上的表现(泛化能力)。然而,在实际应用中,训练和测试数据的分布可能不同(称为分布漂移),这违反了IID假设。在这种情况下,传统的泛化理论可能不再适用,需要引入新的假设或方法来分析和保证模型的泛化能力。
3.7. Weight Decay¶
our first regularization technique
备注
参见: 【知识体系】权重衰减(L2正则化)
3.7.1. Norms and Weight Decay¶
权重衰减不是直接操纵参数的数量,而是通过限制参数可以取的值来进行操作。
- 在深度学习领域,权重衰减通常被称为L2正则化。它是一种通过限制模型参数的取值范围来防止过拟合的技术。
与直接减少参数数量不同,权重衰减通过在损失函数中添加参数值的平方和作为惩罚项,鼓励模型学习较小的权重,从而降低模型复杂度。
这种方法的直观动机是:在所有函数中,恒等于零的函数
f=0被认为是最简单的。因此,可以通过参数值偏离零的程度来衡量函数的复杂度。然而,如何精确地度量函数与零之间的距离并没有唯一的答案。事实上,数学中的某些分支(如泛函分析和Banach空间理论)专门研究此类问题。
备注
【我的理解】前面说了「复杂性的相关概念包括参数的数量和它们允许采用的值的范围」这儿说了「权重衰减不是直接操纵参数的数量,而是通过限制参数可以取的值来进行操作」。所以 权重衰减是通过降低参数的取值范围来降低模型的复杂度 。
【from gpt】当权重特别大时,模型会倾向于去记住数据的每一个细节(包括噪声和随机性),这样它的“复杂度”就会变得很高。但现实世界的数据往往包含噪声,我们希望模型只学到主要规律,而不是所有细节。
【from gpt】较小的权重意味着模型不能对数据中的每一个小特征都过度“记住”,只能学习到大体规律,避免过度拟合。
【from gpt】较小的权重降低了模型对数据的敏感度,让模型的行为更“平滑”,更少受到噪声的干扰,因此降低了模型的复杂度。这种方法通过限制模型的“表达能力”来帮助模型更好地泛化。你可以把较小的权重想象成给模型带上了“安全帽”,不让它太随意地对数据做出过度反应。
备注
在实践中,权重衰减已成为训练参数化机器学习模型时最广泛使用的正则化技术之一。通过在损失函数中添加L2正则项,模型的权重被迫减小,从而限制模型的复杂度,提升泛化能力。这在一定程度上减少了模型过拟合的问题。
【小结】权重衰减作为一种正则化技术,通过限制模型参数的大小,帮助提高模型的泛化能力,减少过拟合现象。
新的损失函数
L2正则化回归的小批量随机梯度下降的 权重更新
3.7.2. High-Dimensional Linear Regression¶
class Data(d2l.DataModule):
def __init__(self, num_train, num_val, num_inputs, batch_size):
self.save_hyperparameters()
n = num_train + num_val
self.X = torch.randn(n, num_inputs)
noise = torch.randn(n, 1) * 0.01
w, b = torch.ones((num_inputs, 1)) * 0.01, 0.05
self.y = torch.matmul(self.X, w) + b + noise
def get_dataloader(self, train):
i = slice(0, self.num_train) if train else slice(self.num_train, None)
return self.get_tensorloader([self.X, self.y], train, i)
3.7.3. Implementation from Scratch¶
从头开始实现权重衰减
3.7.3.1. Defining L2 Norm Penalty¶
最方便的方法是将所有项平方并求和
def l2_penalty(w):
return (w ** 2).sum() / 2
3.7.3.2. Defining the Model¶
唯一的变化是我们的损失现在包括了惩罚项。
class WeightDecayScratch(d2l.LinearRegressionScratch):
def __init__(self, num_inputs, lambd, lr, sigma=0.01):
super().__init__(num_inputs, lr, sigma)
self.save_hyperparameters()
def loss(self, y_hat, y):
return (super().loss(y_hat, y) +
self.lambd * l2_penalty(self.w))
在包含 20 个示例的训练集上拟合我们的模型,并在包含 100 个示例的验证集上对其进行评估(说明:这儿是想说在较少的训练集上适合用权重衰减):
data = Data(num_train=20, num_val=100, num_inputs=200, batch_size=5)
trainer = d2l.Trainer(max_epochs=10)
def train_scratch(lambd):
model = WeightDecayScratch(num_inputs=200, lambd=lambd, lr=0.01)
model.board.yscale='log'
trainer.fit(model, data)
print('L2 norm of w:', float(l2_penalty(model.w)))
3.7.3.3. Training without Regularization¶
train_scratch(0)
# L2 norm of w: 0.009948714636266232
3.7.3.4. Using Weight Decay¶
train_scratch(3)
# L2 norm of w: 0.0017270983662456274
3.7.4. Concise Implementation¶
默认情况下,PyTorch 同时衰减权重和偏差,但我们可以配置优化器根据不同的策略处理不同的参数。
在这里,我们只为权重( net.weight 参数)设置 weight_decay ,因此偏差( net.bias 参数)不会衰减。
class WeightDecay(d2l.LinearRegression):
def __init__(self, wd, lr):
super().__init__(lr)
self.save_hyperparameters()
self.wd = wd # weight_decay
def configure_optimizers(self):
return torch.optim.SGD([
{'params': self.net.weight, 'weight_decay': self.wd},
{'params': self.net.bias}], lr=self.lr)
这个版本运行速度更快,更容易实现:
model = WeightDecay(wd=3, lr=0.01)
model.board.yscale='log'
trainer.fit(model, data)
print('L2 norm of w:', float(l2_penalty(model.get_w_b()[0])))
# L2 norm of w: 0.013779522851109505
3.7.5. Summary¶
正则化是处理过拟合的常用方法。
经典正则化技术在损失函数中添加惩罚项(训练时)以降低学习模型的复杂性。
保持模型简单的一种特殊选择是使用 L2 惩罚。这导致小批量随机梯度下降算法的更新步骤中的权重衰减。
在实践中,权重衰减功能是在深度学习框架的优化器中提供的。在同一训练循环中,不同的参数集可以有不同的更新行为。
4. Linear Neural Networks for Classification¶
4.1. Softmax Regression¶
4.1.1. Classification¶
统计学家很久以前就发明了一种表示分类数据的简单方法:one-hot 编码。 one-hot 编码是一个向量,其分量与类别一样多。与特定实例类别相对应的组件设置为 1,所有其他组件设置为 0。
4.1.1.1. Linear Model¶
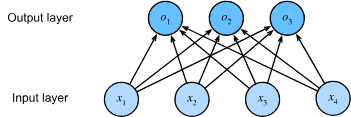
Fig. 4.1.1 Softmax regression is a single-layer neural network.¶
更简洁的表示法:
4.1.1.2. The Softmax¶
未规范化的预测 o 不能直接视作输出的原因:
没有限制这些输出数字的总和为1
输出可能为负值
实现此目标(并确保非负性)的一种方法是 使用指数函数
1:将每个除以它们的总和。这个过程称为 标准化
说明:向量
此外,由于 softmax 操作会保留输入之间的排序关系,我们实际上并不需要真正计算 softmax 的结果,就可以确定哪个类别被分配了最高的概率。
所以如果选择最有可能的类别的话,可以省略 softmax 步骤,即:
4.1.1.3. Vectorization¶
为了提高计算效率并且充分利用GPU, 我们通常会对小批量样本的数据执行矢量化计算(vectorize calculations)。
假设我们读取了一个批量的样本
此外, 假设我们在输出中有 q 个类别。
那么小批量样本的特征为
softmax回归的矢量计算表达式为:
4.1.2. Loss Function¶
4.1.2.1. Log-Likelihood(对数似然)¶
softmax 函数给我们一个向量
例如
假设对于具有特征的数据集
其中索引 i 的样本由:特征向量
计算整个数据集的联合概率(假设每个标签
目标:我们希望最大化
𝑃(𝑌∣𝑋),这实际上是最大似然估计的目标。根据最大似然估计,我们最大化
这其中任意一对标签
备注
注意这儿的 y 是 one-hot 编码
上面这个损失函数通常被叫 交叉熵损失(cross-entropy loss)
4.1.2.2. Softmax and Cross-Entropy Loss¶
1. 交叉熵损失的推导过程¶
softmax 输出的形式:
将 softmax 代入交叉熵损失的定义:
拆分对数:
由于标签 𝑦 是 one-hot 编码或概率分布,标签向量的所有元素加起来总是等于 1,所以可以进一步简化:
2. 梯度推导 (反向传播的核心)¶
对任何
简化:
- 直观理解:
梯度表示模型的预测概率与真实标签之间的差距,即误差信号
3. 更一般的情况: 标签分布为概率分布¶
通常我们假设标签是 one-hot 编码的,如 (0,0,1)。但在某些任务中,标签可能是一个概率分布,如 (0.1,0.2,0.7)
这种情况下,交叉熵损失的计算方式不变:
唯一的区别是 𝑦_𝑗 不再是 0 或 1,而是一个概率值。这种形式更具一般性,允许模型处理更复杂的任务,如知识蒸馏或多标签分类问题。
4. 交叉熵损失的意义: 信息论解释¶
- 交叉熵损失可以从信息论角度理解:
它衡量了真实分布 𝑦 与模型预测分布
直观理解:模型越准确,交叉熵损失越小,因为模型输出分布与真实分布越接近。
- 举例说明:
如果真实分布是 (0,0,1),模型预测 (0.1,0.2,0.7),损失较小。
如果模型预测为 (0.7,0.2,0.1),损失较大,因为模型输出偏离真实类别更远。
5. 关键信息总结¶
交叉熵损失的推导来自最大似然估计,通过 softmax 和对数运算得出。
梯度的形式是模型预测概率与真实标签之间的差距,这是模型参数更新的核心。
信息论角度解释:交叉熵损失衡量模型对真实标签的编码效率,模型越准确,编码代价越小。
泛化性:交叉熵损失不仅适用于 one-hot 标签,还可以处理概率标签,适应更复杂的任务。
4.1.3. Information Theory Basics¶
Information theory(信息论) deals with the problem of encoding, decoding, transmitting, and manipulating information (also known as data).
4.1.3.1. Entropy(熵)¶
信息论的核心思想是量化数据中的信息内容。
在信息论中,该数值被称为分布 P 的熵(entropy)。
可以通过以下方程得到:
One of the fundamental theorems of information theory states that in order to encode data drawn randomly from the distribution P, we need at least
H[P]“nats”to encode it (Shannon, 1948).If you wonder what a “nat” is, it is the equivalent of bit but when using a code with base e rather than one with base 2. Thus, one nat is
4.1.3.2. Surprisal(惊讶度)¶
1. 压缩与预测的联系¶
压缩(compression)与预测(prediction)的关系
核心观点:如果一个数据流很容易预测,那么它也很容易压缩。
例子:举一个极端的例子,流中的每个标记始终采用相同的值。
- 解释:
容易预测:由于数据有很强的规律性,我们可以准确地预测下一个符号是什么。
容易压缩:压缩算法只需记录这个规律,而不用传输大量冗余数据。
- 结论:
“易预测” ⟹ “易压缩”
“难预测” ⟹ “难压缩”
2. 预测失败与“惊讶度”¶
解释:当一个低概率事件发生时,我们会感到“惊讶”。
示例:掷骰子,结果是 7。这会非常令人惊讶,因为 𝑃(7)=0
量化惊讶度-克劳德·香农 (Claude Shannon) 提出了一个公式来衡量这种惊讶程度(Surprisal):
概率越小,惊讶度越大。
如果
𝑃(𝑗)=1,即事件必然发生,惊讶度为 0如果
𝑃(𝑗)=0.01,惊讶度较大。
3. 熵: 期望的惊讶度¶
定义:熵 (Entropy) 是所有可能事件的“平均惊讶度”:
解释:熵衡量了一个系统的“不确定性”。如果系统的熵很高,说明事件分布很分散,难以预测。
- 极端例子:
如果一个事件总是发生 (概率为 1),熵为 0(完全可预测)。
如果所有事件概率均等,熵达到最大(最不确定,最难预测)。
4. 交叉熵: 预测与真实分布的差距¶
- 为什么交叉熵是损失函数:交叉熵衡量模型预测分布
如果模型预测与真实分布接近,交叉熵较小。
如果模型预测远离真实分布,交叉熵较大。
- 为什么交叉熵是损失函数:交叉熵衡量模型预测分布
5. 直观例子¶
假设
真实概率分布 y=(0,0,0,0,0,1) 表示只会掷出 6
模型预测分布为
计算交叉熵损失:
4.1.3.3. Cross-Entropy Revisited¶
结合上面的惊讶度(Surprisal)的理解
- 可以把 熵H(P) 看成
一个知道真实概率的人在经历概率事件时的惊讶度(Surprisal) 直观理解:
如果我们对数据的分布非常了解 (即 𝑃 是我们预测的分布),那么熵就是我们对未来事件的“平均惊讶度”。
这是最佳压缩的理论极限。
- 可以把 熵H(P) 看成
- 那么 交叉熵H(P, Q) 描述的是我们用主观概率分布 𝑄 预测真实分布 𝑃 数据时的平均惊讶度。
直观解释:
真实分布 𝑃 表示实际发生的情况,而模型预测 𝑄 代表我们对数据的“主观理解”。
如果模型 𝑄 偏离了真实分布 𝑃,我们在看到真实数据时会感到更“惊讶”。
【示例】
真实分布 𝑃:骰子掷出每个面的概率均为 𝑃(𝑗)=1/6
模型分布 𝑄 (预测分布):模型错误地认为骰子掷出6的概率是 𝑄(6)=0.5,其他面的概率是 𝑄(𝑗)=0.1。
- 计算熵和交叉熵:
熵:
交叉熵:
# 熵(1.7918)
torch.log(torch.tensor(6))
# 交叉熵(2.0343)
-5/6 * torch.log(torch.tensor(0.1)) -1/6 * torch.log(torch.tensor(0.5))
5/6 * torch.log(torch.tensor(10)) + 1/6 * torch.log(torch.tensor(2))
备注
【解读】当 𝑃=𝑄(模型预测准确) 时,交叉熵达到最小值,此时:𝐻(𝑃,𝑃)=𝐻(𝑃) ❇️=》也就是说:真实分布和预测分布一致时,交叉熵等于熵。
- 以从两个角度理解交叉熵分类目标函数:
最大化观察到的数据的似然 (likelihood);
最小化模型对真实标签的惊讶度(即减少编码标签所需的比特数)。
4.2. The Image Classification Dataset¶
主要讲了 torchvision 的基本使用
4.3. The Base Classification Model¶
4.3.1. The Classifier Class¶
定义Classifier类
class Classifier(d2l.Module): #@save
"""The base class of classification models."""
def validation_step(self, batch):
Y_hat = self(*batch[:-1])
self.plot('loss', self.loss(Y_hat, batch[-1]), train=False)
self.plot('acc', self.accuracy(Y_hat, batch[-1]), train=False)
使用随机梯度下降优化器,在小批量上运行
@d2l.add_to_class(d2l.Module) #@save
def configure_optimizers(self):
return torch.optim.SGD(self.parameters(), lr=self.lr)
4.3.2. Accuracy¶
@d2l.add_to_class(Classifier) #@save
def accuracy(self, Y_hat, Y, averaged=True):
"""Compute the number of correct predictions."""
Y_hat = Y_hat.reshape((-1, Y_hat.shape[-1]))
preds = Y_hat.argmax(axis=1).type(Y.dtype)
compare = (preds == Y.reshape(-1)).type(torch.float32)
return compare.mean() if averaged else compare
4.4. Softmax Regression Implementation from Scratch¶
4.4.1. The Softmax¶
计算 softmax 需要三个步骤:
i) 每一项求幂
ii) 每行求和以计算每个示例的归一化常数
iii) 将每一行除以其归一化常数,确保结果总和为 1
4.4.2. The Model¶
class SoftmaxRegressionScratch(d2l.Classifier):
def __init__(self, num_inputs, num_outputs, lr, sigma=0.01):
super().__init__()
self.save_hyperparameters()
self.W = torch.normal(0, sigma, size=(num_inputs, num_outputs),
requires_grad=True)
self.b = torch.zeros(num_outputs, requires_grad=True)
def parameters(self):
return [self.W, self.b]
网络如何将每个输入映射到输出:
@d2l.add_to_class(SoftmaxRegressionScratch)
def forward(self, X):
X = X.reshape((-1, self.W.shape[0]))
return softmax(torch.matmul(X, self.W) + self.b)
4.4.3. The Cross-Entropy Loss¶
创建了示例数据y_hat其中包含 2 个示例 预测 3 个类别的概率及其相应的标签 y
y = torch.tensor([0, 2])
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y_hat[[0, 1], y]
# tensor([0.1000, 0.5000])
对所选概率的对数进行平均来实现交叉熵损失函数:
def cross_entropy(y_hat, y):
y2 = y_hat[list(range(len(y_hat))), y] # tensor([0.1000, 0.5000])
return -torch.log(y2).mean()
cross_entropy(y_hat, y)
# tensor(1.4979)
定义损失函数:
@d2l.add_to_class(SoftmaxRegressionScratch) def loss(self, y_hat, y): return cross_entropy(y_hat, y)
4.4.4. Training¶
data = d2l.FashionMNIST(batch_size=256)
model = SoftmaxRegressionScratch(num_inputs=784, num_outputs=10, lr=0.1)
trainer = d2l.Trainer(max_epochs=10)
trainer.fit(model, data)
4.4.5. Prediction¶
X, y = next(iter(data.val_dataloader()))
preds = model(X).argmax(axis=1)
preds.shape
# torch.Size([256])
我们对错误标记的图像更感兴趣。通过将它们的实际标签(文本输出的第一行)与模型的预测(文本输出的第二行)进行比较来可视化它们:
wrong = preds.type(y.dtype) != y
X, y, preds = X[wrong], y[wrong], preds[wrong]
labels = [a+'\n'+b for a, b in zip(
data.text_labels(y), data.text_labels(preds))]
data.visualize([X, y], labels=labels)

4.5. Concise Implementation of Softmax Regression¶
4.5.1. Defining the Model¶
内置的__call__方法就会调用forward
class SoftmaxRegression(d2l.Classifier): #@save
"""The softmax regression model."""
def __init__(self, num_outputs, lr):
super().__init__()
self.save_hyperparameters()
self.net = nn.Sequential(nn.Flatten(),
nn.LazyLinear(num_outputs))
def forward(self, X):
return self.net(X)
4.5.2. Softmax Revisited¶
- 原始 softmax 计算方式在实际实现中可能存在数值稳定性问题,主要包括:
上溢 (Overflow):如果
下溢 (Underflow):如果所有
- 数值不稳定性的具体原因
计算机表示浮点数的范围有限。例如,单精度浮点数的表示范围约为
如果最大的
[-90, 90],结果就会变得不稳定。
- 解决方案
核心思想:为了避免溢出或下溢,可以通过平移 logits,使得最大的 logits 变为 0,从而让所有 logits 都位于一个较小的范围内。
- 具体方法:
设
从所有 logits 中减去
- 分析
防止上溢:因为
(0, 1]防止下溢:如果
但我们可以利用 softmax 和交叉熵的组合,避免直接计算
推理过程
@d2l.add_to_class(d2l.Classifier) #@save
def loss(self, Y_hat, Y, averaged=True):
Y_hat = Y_hat.reshape((-1, Y_hat.shape[-1]))
Y = Y.reshape((-1,))
return F.cross_entropy(
Y_hat, Y, reduction='mean' if averaged else 'none')
4.5.3. Training¶
data = d2l.FashionMNIST(batch_size=256)
model = SoftmaxRegression(num_outputs=10, lr=0.1)
trainer = d2l.Trainer(max_epochs=10)
trainer.fit(model, data)
4.6. Generalization in Classification¶
4.6.1. The Test Set¶
1. 经验误差 (Empirical Error)¶
公式解析:
其中
含义:模型在测试集
指示函数的直观理解:
2. 总体误差 (Population Error)¶
公式解析:
其中
含义:模型在整个潜在数据分布中分类错误的期望概率。
问题:无法直接计算,因为真实分布
由于测试集
此外,由于我们感兴趣的量
3. 中心极限定理 (CLT) 和误差收敛速度¶
我们关心的随机变量
Bernoulli 分布的随机变量单个样本误差的方差是:
虽然
中心极限定理表明,当样本量
- 直观含义:
想把测试误差减少一半,需要 4 倍的样本量。
如果要将误差减少 100 倍,需要 10,000 倍的样本量。
- 例如,如果希望误差的估计精确到
±0.01,大约需要 2,500 个样本。 Bernoulli 分布的随机变量单个样本误差的方差是:
方差
如果希望误差波动在
解得 n=2500
- 例如,如果希望误差的估计精确到
通常情况下,这种
中心极限定理的核心思想:中心极限定理告诉我们,无论总体分布如何,如果从总体中抽取大量独立同分布的随机样本,并计算样本均值,这个样本均值的分布将近似服从正态分布 (Normal Distribution),只要样本数量足够大。
4. Hoeffding 不等式和有限样本误差界¶
前面的分析主要针对渐近情况,即随着样本数量趋近无穷时的行为。
然而,幸运的是,由于我们的随机变量是有界的,我们可以通过 Hoeffding (1963) 提出的一个不等式得到有限样本下的有效界限:
为确保在 95% 置信水平下,
这种趋势在统计学中普遍存在。适用于有限样本的保证通常比渐近分析更保守一些。然而,这两者给出的数值差距不大,反映出渐近分析在实际应用中仍然具有相当的参考价值,即使它们无法提供完全的保证。
解释:这条不等式提供了在有限样本下的误差估计。
t 表示允许误差的容忍范围。
当
t = 0.01(即希望误差在±0.01范围内)时,需要约 15,000 个样本,比中心极限定理估计的 10,000 样本略多。结论:有限样本下的误差估计比无穷样本下略保守,但两者差距不大,表明中心极限定理提供了很好的估计。
4.6.2. Test Set Reuse¶
分析:测试集重用问题与风险
核心观点¶
- 测试集是机器学习模型评估的基准,但重用测试集可能带来严重的问题,主要涉及到:
假发现率(False Discovery Rate)问题
自适应过拟合(Adaptive Overfitting)风险
1) 假发现率问题¶
背景:在评估模型
- 风险:
每次模型评估都存在 5% 的误导风险(置信水平95%)。
如果在相同测试集上评估 k 个模型,即使每个模型独立地有95%置信度,整体出现至少一个误导结果的概率大大增加。
举例:当
影响:错误的模型可能被误选为最佳模型,导致实际性能不佳。
2) 自适应过拟合¶
背景:如果模型
- 风险:
测试集在评估
这破坏了机器学习模型评估的核心原则,即模型不能“见过”测试集数据。
例子:在 Kaggle 比赛中,如果多次在私有测试集上提交模型并调整参数,最终的模型可能只是在测试集上表现很好,而在真实场景中表现较差。
本质:模型不断根据测试集反馈优化,测试集逐渐退化为训练集的延伸,无法有效反映模型的真实泛化能力。
缓解策略与实践建议¶
避免重复使用同一测试集。策略:构建多个独立的测试集,每轮评估后将旧测试集降级为验证集,避免反复使用同一批数据。
考虑多重假设检验。方法:在评估多个模型时,采用 Bonferroni校正 等方法降低假发现率。例如,对于 k 个模型评估,将置信水平调整为
限制对测试集的访问频率。实践:设置明确的测试集访问次数上限(如最多3次),严格记录每次访问目的。在重大模型评估前,尽量减少对测试集的接触,仅在最终模型准备发布前使用测试集。
加大数据集规模。理由:大数据集更能抵抗过拟合风险,即使有一定程度的信息泄露,大规模数据仍能提供可靠评估。
4.6.3. Statistical Learning Theory¶
核心观点¶
模型泛化的根本难题在于如何保证训练误差接近真实误差。
解决路径:通过数学工具(如VC维度)建立泛化误差的上界,量化模型复杂性与数据样本数量之间的关系。
目标:实现一致收敛性,确保模型在训练集和测试集上的误差差距在可控范围内。
主要问题拆解¶
泛化问题的本质:“测试集是我们唯一的参考”:机器学习模型的性能评估依赖于测试集,但测试集的结果仅能反映事后泛化能力,无法提供事前泛化保证。困难点:即使一个模型在测试集上表现良好,也无法保证下一个模型(f_2, f_3, …)能持续泛化。
泛化误差与样本误差的差距:核心问题:经验误差
模型类
解决思路:一致收敛性与VC维度¶
1) 一致收敛性(Uniform Convergence)¶
目标:确保所有模型在训练集和真实分布上的误差收敛到同一个小范围内。
定义:对于模型类中的所有模型
其中
- 挑战:
过于灵活的模型类(如记忆机,能记住训练集上所有数据但泛化性极差)很难满足一致收敛性。
过于刚性的模型类则风险在于欠拟合,难以捕捉训练数据的规律。
平衡:学习理论的目标是在 模型灵活性(高方差)和模型刚性(高偏差) 之间找到平衡点。
2) Vapnik-Chervonenkis (VC) 维度¶
VC 维度:衡量模型类的复杂性,反映模型拟合任意数据点的能力。
VC 维度提供了一种量化模型类复杂性的方法,但在实际应用中可能过于保守。
现实意义与应用¶
- 经验误差 vs. 泛化误差
小数据场景:训练误差低并不代表模型能泛化,可能是过拟合。
大数据场景:随着数据量
n增加,经验误差逐渐收敛到真实误差。
- 工程实践
深度学习:复杂模型往往需要大量样本,即使训练集误差接近 0,也不能简单假设泛化误差很低。
自动驾驶等领域:高风险场景下通常采用更大的数据集和多重交叉验证,降低泛化误差的不确定性。
4.7. Environment and Distribution Shift¶
分布漂移(Distribution Shift)
4.7.1. Types of Distribution Shift¶
- 引言:
提出分布漂移的概念,指出训练数据和测试数据可能来自不同的分布,直接影响模型性能。
强调在缺乏关于分布关系的假设下,鲁棒分类器的学习是不可能的。
通过二分类问题(猫狗分类)引出一个极端例子:如果输入分布保持不变,但标签完全反转,将无法区分分布是否发生变化。
- 转折:
说明在适当假设下,可以检测分布漂移,并可能动态调整模型以提升性能。
- 核心思想
分布漂移不可避免,但在合理假设下,可以检测和适应漂移。
关键是理解漂移来源(特征变化、标签变化或标签定义变化),并选择合适的算法来应对。
协变量漂移是最常研究的方向,因为特征分布变化直观且更易被监测到。
标签漂移更具挑战,通常需要在低维标签空间中操作,而不是直接在高维特征空间中处理漂移。
概念漂移最复杂,通常依赖外部知识或元学习方法来逐渐适应。
4.7.1.1. Covariate Shift¶
定义: 特征的分布
示例:训练集是实物照片,测试集是卡通图像,特征分布(图片风格)变了,但猫狗的本质定义不变。
解释:协变量漂移常见于因果关系中,特征
4.7.1.2. Label Shift¶
定义: 标签分布
示例:不同疾病的患病率变化,但疾病表现出的症状不变。
- 解释:
标签漂移通常出现在标签 y 影响特征
操作标签的模型(低维)通常更易处理这种情况,而操作特征的模型(高维)难度较大。
4.7.1.3. Concept Shift¶
定义: 标签本身的定义发生变化,即
- 示例:
不同地区对同一种软饮料有不同称呼(如 “pop” 和 “soda”)。
疾病诊断标准或时尚趋势随时间和地域变化。
- 解释:
概念漂移难以察觉,因为标签定义可能随时间或地理位置逐渐变化。
在自然语言处理或机器翻译中,概念漂移尤为明显。
4.7.2. Examples of Distribution Shift¶
4.7.2.1. Medical Diagnostics¶
医疗诊断(Medical Diagnostics)
背景:目标是开发癌症检测算法,使用健康人和病人的血液样本进行训练。
问题:由于健康男性样本难以收集,创业公司选择了大学生血样作为对照组。
结果:分类器可以轻松区分健康和病人群体,但这是因为大学生和老年病人之间存在大量无关变量(年龄、激素水平、生活方式等)差异,而非疾病相关特征。
本质:极端协变量漂移(Covariate Shift),健康对照组和真实病人群体特征存在巨大差异,导致模型在真实世界表现不佳。
启示:数据采样过程必须匹配真实应用环境。不能仅为解决数据稀缺问题随意选择不具代表性的样本。
4.7.2.2. Self-Driving Cars¶
背景:公司希望用游戏引擎合成数据训练道路探测器,以减少标注数据的成本。
问题:在引擎测试数据上表现良好,但在真实环境中完全失败。
原因:道路纹理在游戏引擎中过于简单,并且所有道路都使用相同纹理。模型学习到的是纹理差异,而非真正的道路特征。
类似案例:美军曾试图通过航拍照片训练坦克探测器,但模型实际上只是学会了区分早晨和中午的树影差异。
本质:概念漂移或协变量漂移, 模型学到了错误特征,导致真实场景下表现不佳。
启示:合成数据需尽量贴近现实。避免训练数据和实际应用场景间存在严重差距。需要混合多种真实和合成数据来源,以减少模型对无关特征的依赖。
4.7.2.3. Nonstationary Distributions¶
非平稳分布(Nonstationary Distributions)
定义: 分布随时间缓慢变化,模型未能及时更新。
- 典型案例:
广告模型未及时更新,新设备(如iPad)推出后未纳入训练,模型失效。
垃圾邮件过滤器过时,新型垃圾邮件逃过检测。
产品推荐系统滞后,仍推荐圣诞帽,未能适应季节变化。
本质:分布缓慢漂移, 随着时间推移模型性能逐渐下降。
启示:模型需要定期更新和重新训练 以适应环境变化。引入在线学习机制,使模型可以持续学习新数据。
4.7.3. Correction of Distribution Shift¶
本节是比较高级的功能,不理解也不影响后面章节的学习
4.7.3.1. Empirical Risk and Risk¶
风险定义与训练目标:训练模型时,我们的目标是使模型在训练数据上的损失最小化。
1. 经验风险 (Empirical Risk)¶
经验风险最小化, 即在训练数据集上计算损失并最小化平均损失。
2. 真实风险 (True Risk)¶
真实风险考虑的是整个数据分布
4.7.3.2. Covariate Shift Correction¶
定义:特征的分布
问题:训练数据来自源分布
解决方案:通过重加权 (Re-weighting) 技术调整训练数据的权重,使其更符合目标分布。
即,将每个样本的权重乘以
- 实际操作步骤:
训练一个分类器,区分目标分布
使用逻辑回归计算
在模型训练时,对每个样本
4.7.3.3. Label Shift Correction¶
解决方案:通过计算标签分布 p(y) 和 q(y) 的比值
公式推导:
4.7.3.4. Concept Shift Correction¶
问题:例如,从区分猫和狗转变为区分白色和黑色动物,这种变化很难通过简单的方法校正。
- 解决方案:
对于渐变的漂移,可以在现有模型上进行少量更新,而非从头训练新模型。
对于剧烈的漂移,通常需要重新收集数据和标签,重新训练模型。
- 实际应用示例:
广告推荐:用户兴趣变化,新产品上线。
交通摄像头:镜头老化导致图像质量下降。
新闻推荐:新闻内容不断更新,新事件出现。
通过持续学习 (Continual Learning) 或迁移学习 (Transfer Learning) 应对概念漂移。
4.7.4. A Taxonomy of Learning Problems¶
4.7.4.1. Batch Learning¶
- 概念:在批量学习中,我们拥有一个完整的训练数据集
模型 :math`f(mathbf{x})` 是在所有数据都已知的情况下训练完成的。
训练完成后,模型部署在真实环境中,不再进行更新(除非有重大错误或特殊情况)。
- 概念:在批量学习中,我们拥有一个完整的训练数据集
示例:训练一个猫狗分类器,用于智能猫门。当模型训练完成并安装在客户家中后,它不会再改变或学习新的数据。
- 特点:
训练和推理是分开的。
适用于静态、不经常变化的任务。
训练数据与未来数据分布一致时效果最好。
4.7.4.2. Online Learning¶
- 概念:数据逐个到达,模型需要逐步学习,每次接收一个样本
在观察到标签
在得到标签后,模型根据损失进行更新,逐渐变得更好。
- 概念:数据逐个到达,模型需要逐步学习,每次接收一个样本
示例:股票价格预测:每天预测第二天的股价,等到实际价格出来后,再更新模型,调整预测方式。
- 流程:
使用模型
观察真实标签
更新模型
- 特点:
持续学习和更新模型
适用于环境动态变化、数据不断流入的场景
可应对概念漂移(concept shift)
4.7.4.3. Bandits¶
- 概念:
多臂老虎机是一类特殊的在线学习问题
不同于连续参数模型(如神经网络),Bandit 只有有限个动作或选择
目标是找到收益最高的“拉杆”或动作
- 示例:
在线广告推荐:在多个广告中选择一个展示,观察点击率,不断调整选择策略。
- 特点:
只需在有限选项中进行决策
通常具有较强的理论保证和优化策略
算法更简单,但问题范围更狭窄
4.7.4.4. Control¶
- 概念:
环境会记住模型的决策,下一次的观测值依赖于之前的行为。
不一定是对抗性的,但模型的行为会影响未来状态。
- 示例:
咖啡机的温度控制器:是否继续加热取决于当前温度以及之前的加热状态。
新闻推荐系统:用户是否点击新闻取决于之前推荐的内容。
- 特点:
模型需要记忆和考虑过去的行为。
经常使用控制理论方法,如 PID 控制器。
可用于环境交互式决策问题。
4.7.4.5. Reinforcement Learning¶
- 概念:
强化学习是在复杂环境中进行决策的更高级形式。
环境可能是合作的(例如多玩家合作游戏),也可能是竞争的(如象棋、围棋)。
模型需要通过与环境交互,不断学习以最大化累积奖励。
- 示例:
游戏 AI:在象棋、围棋或电子竞技游戏中,自主学习对抗策略。
自动驾驶:其他车辆的行为会受到自动驾驶车辆的影响。
- 特点:
适用于复杂、有记忆的动态环境。
强调长期策略和累积奖励。
环境的反馈(奖励或惩罚)决定模型更新方式。
4.7.4.6. Considering the Environment¶
- 核心思想:
不同环境下,模型的表现和策略可能完全不同
在静态环境中,一个有效的策略可能在动态环境中失效
环境的变化速度和方式,决定了需要使用哪种学习方法
- 示例:
金融市场:套利机会一旦被发现并利用,市场会迅速调整,套利机会消失。
推荐系统:用户兴趣随时间变化,需要动态更新模型。
- 解决方法:
- 缓慢变化的环境:
约束模型的更新速度,使其缓慢适应环境变化。
- 快速但偶尔变化的环境:
在环境突然变化时允许模型迅速调整,但日常变化较少。
总结¶
批量学习:静态、一次性训练。
在线学习:逐步更新模型,适应动态环境。
Bandit:有限动作选择问题,优化奖励。
控制:环境会记住模型的行为,状态依赖历史。
强化学习:复杂动态环境中通过奖励学习策略。
5. Multilayer Perceptrons¶
5.1. Multilayer Perceptrons¶
5.1.2. Activation Functions¶
激活函数通过计算加权和并进一步添加偏差来决定是否应该激活神经元。
它们是可微分算子,用于将输入信号转换为输出,但大多数都增加了非线性。
5.1.2.1. ReLU Function
5.1.2.2. Sigmoid Function
5.1.2.3. Tanh Function
5.2. Implementation of Multilayer Perceptrons¶
5.2.1. Implementation from Scratch¶
5.2.1.1. Initializing Model Parameters:
class MLPScratch(d2l.Classifier):
def __init__(self, num_inputs, num_outputs, num_hiddens, lr, sigma=0.01):
super().__init__()
self.save_hyperparameters()
self.W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens) * sigma)
self.b1 = nn.Parameter(torch.zeros(num_hiddens))
self.W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs) * sigma)
self.b2 = nn.Parameter(torch.zeros(num_outputs))
5.2.1.2. Model:
def relu(X):
a = torch.zeros_like(X)
return torch.max(X, a)
@d2l.add_to_class(MLPScratch)
def forward(self, X):
X = X.reshape((-1, self.num_inputs))
H = relu(torch.matmul(X, self.W1) + self.b1)
return torch.matmul(H, self.W2) + self.b2
5.2.1.3. Training:
# 训练循环与 softmax 回归完全相同
model = MLPScratch(num_inputs=784, num_outputs=10, num_hiddens=256, lr=0.1)
data = d2l.FashionMNIST(batch_size=256)
trainer = d2l.Trainer(max_epochs=10)
trainer.fit(model, data)
5.2.2. Concise Implementation¶
5.2.2.1. Model:
# 和之前的区别是这儿有两个全连接层(第一个隐藏层,第二个输出层)
class MLP(d2l.Classifier):
def __init__(self, num_outputs, num_hiddens, lr):
super().__init__()
self.save_hyperparameters()
self.net = nn.Sequential(
nn.Flatten(),
nn.LazyLinear(num_hiddens),
nn.ReLU(),
nn.LazyLinear(num_outputs)
)
5.2.2.2. Training:
# 与实现 softmax 回归时完全相同。这种模块化使我们能够将有关模型架构的问题与其他无关的因素分离开来
model = MLP(num_outputs=10, num_hiddens=256, lr=0.1)
trainer.fit(model, data)
5.3. Forward Propagation, Backward Propagation, and Computational Graphs¶
5.3.1. Forward Propagation¶
前向传播是神经网络的核心计算步骤,它指的是按照从输入层到输出层的顺序,计算和存储中间变量(包括输出)。简单来说,就是把输入数据一层层地传递,最终得到输出结果。
1. 输入与权重矩阵¶
假设我们有一个输入样本
隐藏层的权重矩阵
z 是隐藏层的线性变换结果,长度为 h,表示隐藏层有 h 个神经元
2. 激活函数与隐藏层输出¶
应用一个激活函数
h 是隐藏层的激活输出,长度为 h
激活函数
3. 输出层计算¶
隐藏层输出
4. 计算损失¶
输出
L 是单个样本的损失值,反映了模型输出与真实值之间的差距。
5. 正则化项¶
为了防止过拟合,我们可以引入
其中
6. 目标函数¶
最终的目标函数是:
J 表示带正则化的损失函数,是模型需要最小化的目标
在训练过程中,我们优化的是 J,以便在损失与模型复杂度之间取得平衡
5.3.2. Computational Graph of Forward Propagation¶
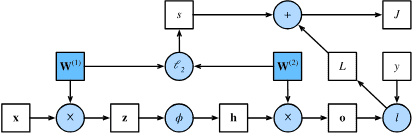
Fig. 5.3.1 Computational graph of forward propagation.¶
其中正方形表示变量,圆圈表示运算符。
左下角表示输入,右上角表示 输出。
5.3.3. Backpropagation¶
反向传播是神经网络中用于计算参数梯度的方法。
简单来说,它是通过从输出层向输入层的反向遍历,根据微积分中的链式法则逐步计算梯度的过程。
1. 链式法则¶
2. 反向传播目标¶
假设一个简单的单隐藏层神经网络,参数包括:
3. 逐步计算过程¶
计算目标函数对损失项和正则化项的梯度
计算对输出层变量
计算正则化项对参数的梯度
计算输出层参数
输出层权重梯度等于 损失对输出的梯度 乘以 隐藏层激活输出 ,再加上 正则化项
计算隐藏层输出
计算隐藏层激活前变量
这里使用逐元素乘法
计算输入层参数
最终,输入层权重的梯度是损失对
小结¶
反向传播逐层计算梯度,从输出层反向回溯到输入层。
每一步都应用链式法则,将损失项和正则化项对参数的梯度进行累积。
最终计算出的梯度用于更新模型参数,逐步降低目标函数 J,实现模型优化。
5.3.4. Training Neural Networks¶
训练神经网络时,前向传播和后向传播相互依赖。
正向传播:按计算图的依赖关系,从输入层开始,一直到输出层,计算并存储中间变量。
反向传播:在反方向上,从输出层回到输入层,利用正向传播中存储的中间变量计算梯度。
训练过程的交替进行¶
模型初始化:先初始化模型参数。
- 交替进行:
正向传播:计算输出和损失函数,存储中间变量。
反向传播:利用存储的中间变量,计算梯度并更新模型参数。
关键点:反向传播重用正向传播存储的中间变量,避免重复计算。
内存占用¶
中间变量的保留:正向传播产生的中间变量需要保留,直到反向传播完成。这是训练阶段内存占用较高的主要原因之一。
- 内存消耗的影响因素:
网络层数:层数越多,中间变量越多,占用的内存越大。
批大小 (batch size):批量大小越大,中间变量的数量和大小也会增加。
备注
在训练神经网络时,一旦模型参数初始化,我们就交替前向传播和反向传播,使用反向传播给出的梯度来更新模型参数。请注意,反向传播重用前向传播中存储的中间值以避免重复计算。结果之一是我们需要保留中间值,直到反向传播完成。这也是训练比普通预测需要更多内存的原因之一。
5.3.5. Summary¶
前向传播顺序计算并存储神经网络定义的计算图中的中间变量。它从输入层进行到输出层。
反向传播以相反的顺序顺序计算并存储神经网络内中间变量和参数的梯度。
在训练深度学习模型时,前向传播和反向传播是相互依赖的,并且训练需要的内存明显多于预测。
5.4. Numerical Stability and Initialization¶
5.4.1. Vanishing and Exploding Gradients¶
核心问题:在深度神经网络中,随着网络层数增加,反向传播过程中梯度可能变得非常小(消失)或非常大(爆炸)。这会导致模型难以收敛或学习速度极慢。
1. 数学背景与直观理解¶
考虑一个深度网络
L layers,输入 x 和输出 o 。With each layer l defined by a transformation
其隐藏层输出为
如果所有隐藏层的输出和输入都是向量,我们可以写成
直观理解:
梯度爆炸:梯度非常大,参数更新太剧烈,模型无法收敛,甚至损坏。
梯度消失:梯度接近零,参数更新缓慢或不更新,学习停滞。
2. 梯度消失(Vanishing Gradient)¶
- 主要原因:激活函数的选择,尤其是 sigmoid 函数。
sigmoid 函数在输入值非常大或非常小时,导数接近零。
导致反向传播过程中,梯度层层相乘,最终趋近于零。
- 解决方案:
使用 ReLU(Rectified Linear Unit)激活函数:
ReLU 函数在正区间梯度为 1,在负区间梯度为 0,避免了梯度消失问题。
3. 梯度爆炸(Exploding Gradient)¶
- 主要原因:权重矩阵
层与层之间权重矩阵乘积可能导致梯度指数级增长。
权重矩阵的特征值较大,导致整体梯度爆炸。
- 主要原因:权重矩阵
示例-多次相乘后,矩阵值爆炸:
M = torch.normal(0, 1, size=(4, 4))
for i in range(100):
M = M @ torch.normal(0, 1, size=(4, 4))
print(M)
# 输出
tensor([[-7.9222e+22, -1.1940e+23, 1.0915e+23, 1.0751e+23],
[ 3.8837e+22, 5.8528e+22, -5.3505e+22, -5.2693e+22],
[-1.9618e+22, -2.9577e+22, 2.7037e+22, 2.6641e+22],
[ 3.0163e+22, 4.5455e+22, -4.1554e+22, -4.0923e+22]])
- 解决方案:
梯度裁剪(Gradient Clipping):设置梯度阈值,超过阈值的梯度会被缩放。
权重初始化:使用 Xavier 初始化或 He 初始化,保持初始梯度稳定。
4. 对称性破坏问题(Breaking Symmetry)¶
- 问题描述:
网络初始化时,如果所有权重相等,隐藏层神经元将输出相同的值。
这种对称性会导致网络只能学习到有限的特征,浪费网络容量。
- 解决方案:
在初始化时,引入随机性,确保权重不同。
Dropout 正则化方法可以帮助打破对称性,使不同神经元学习不同的特征。
5.4.2. Parameter Initialization¶
解决(或至少减轻)上述问题的一种方法是对神经网络中的参数初始化方法的处理。
5.4.2.1. Default Initialization¶
如果不特别指定,深度学习框架会使用默认的随机初始化,通常是从正态分布中随机抽取权重。这个方法在中等规模问题中效果不错,但对于非常深的网络可能会导致梯度问题。
5.4.2.2. Xavier Initialization¶
Xavier初始化(或Glorot初始化)是一种专门设计来保持前向和反向传播中输出的方差相对稳定的方法。
目标:防止信号在层与层之间传递时逐渐消失或爆炸。
- 方法推导:
假设一个无激活函数的全连接层,输出
假设权重
输入
计算输出方差:
and the variance:
为了保持输出的方差固定,需要满足条件:
在反向传播时,类似的方差条件需要满足:
由于无法同时满足两个条件,Xavier初始化取折中:
实操¶
如果从正态分布中抽取权重:
如果使用均匀分布
- 实践效果
尽管推导假设没有使用激活函数,但在实际网络中,即使有非线性激活,Xavier初始化依然表现良好。
它解决了一部分梯度消失/爆炸问题,使得网络更容易收敛。
5.4.3. Summary¶
梯度消失和爆炸是深度网络中的常见问题。
在参数初始化时需要非常小心,以确保梯度和参数保持良好的控制。需要初始化启发法来确保初始梯度既不太大也不太小。随机初始化是确保优化之前打破对称性的关键。
Xavier 初始化表明,对于每一层,任何输出的方差不受输入数量的影响,并且任何梯度的方差不受输出数量的影响。 ReLU 激活函数缓解了梯度消失问题。这可以加速收敛。
5.5. Generalization in Deep Learning¶
5.5.1. Revisiting Overfitting and Regularization¶
引入背景与传统认知¶
- “无免费午餐定理”(no free lunch theorem)
强调所有学习算法在某些分布上表现更好,而在其他分布上表现更差。
根据Wolpert(1995)提出的这一理论,任何学习算法在某些数据分布上会表现得更好,在其他分布上则可能更差。
这意味着对于有限的训练集,模型需要依赖于一些假设来达到人类级别的性能,而这些假设被称为归纳偏好。
- 归纳偏置(inductive biases)
它指的是模型对具有某些特性的解决方案的偏好。例如,深层多层感知器(MLP)倾向于通过组合简单函数来构建复杂函数。
为了弥补有限训练数据的局限性),即类似人类对世界的思考方式,从而偏向具有特定性质的解决方案。
- 两阶段训练
首先是使模型尽可能好地拟合训练数据,其次是在保留的测试数据集上估计泛化误差。
泛化差距是指训练误差与测试误差之间的差异;当这个差距较大时,表示模型过拟合了训练数据。
- 过拟合
经典观点:如果模型过于复杂,可能会导致过拟合。此时可以通过减少特征数量、非零参数的数量或参数大小来解决这个问题。
过拟合是训练误差和测试误差之间的差距,当模型复杂度过高时,容易发生过拟合。
深度学习的反常现象¶
- 深度学习中的过拟合:
不同于经典的观点,深度学习打破了经典的“模型复杂度 vs. 误差”的简单关系。深度学习模型往往足够表达力强,以至于可以完美拟合每个训练样本。
尽管如此,我们仍可以通过增加模型的表达能力(如添加层数、节点数或延长训练周期)来减少泛化误差,这与传统认知相悖。
- 反直觉现象
传统观点认为,模型在复杂度轴的极端位置时,泛化误差会增加,因此需要通过正则化或降低模型复杂度来减少过拟合。
在深度学习中,即使模型完全拟合训练数据,增加模型复杂度(如增加层数或节点)反而可能减少泛化误差。
这种现象被称为双重下降(double descent)。
双重下降现象:随着模型复杂度的增加,泛化差距起初会增大,但之后又会减小。这种现象表明,模型复杂度与泛化性能之间的关系并非单调。
深度学习实践者的工具包:包括一些看似限制模型的方法(如正则化),以及一些看似增强模型表达能力的方法,所有这些都是为了减轻过拟合的问题。
挑战传统理论¶
深度学习的成功使得传统学习理论难以解释其泛化能力。尽管可以使用
关键矛盾在于,神经网络即使能够拟合任意标签数据,实际测试误差依然可能较低,说明现有理论存在局限性。
这表明,对于深度学习模型,我们需要新的理论框架来理解其泛化能力。
关键词解析¶
Inductive Bias:模型在学习过程中偏向于特定类型的解决方案或假设,有助于提高泛化能力。
Generalization Gap:训练误差与测试误差之间的差距。
Double Descent:模型复杂度增加时,误差先下降再上升,随后再次下降的现象,打破了经典“U型”误差曲线的概念。
VC Dimension/Rademacher Complexity:衡量模型复杂度的经典理论工具,在深度学习领域面临解释能力不足的问题。
5.5.2. Inspiration from Nonparametrics¶
探讨了深度学习与非参数模型(nonparametric models)之间的关系,挑战了将深度神经网络仅视为参数化模型的直觉,并展示了如何从非参数视角来看待神经网络的行为。
深度学习的参数化与非参数化对比¶
深度学习模型拥有大量的参数,因此直观上看,它们是参数化模型。在训练过程中,模型的参数不断更新,保存时也写入参数。
然而,文本指出,尽管神经网络有大量参数,从某些角度来看,它们的行为更像是非参数模型。这种思维方式可以帮助我们更好地理解神经网络的泛化能力和训练机制。
非参数模型的定义¶
非参数模型的复杂度通常随着数据量的增加而增加。经典的非参数模型例子是 k-最近邻算法 (k-nearest neighbor,KNN)。
KNN模型在训练阶段只是记住数据集,而在预测时,通过寻找最接近的训练点来进行分类或回归。
当
k=1时,KNN模型可以实现零训练误差,但这并不意味着它没有泛化能力。事实上,在某些条件下,1-最近邻算法会随着数据量的增加而收敛到最优预测器。
度量函数和归纳偏置¶
1-最近邻算法的关键是距离函数(distance function),也即如何将数据转换为特征向量(featurizing data)。
不同的距离度量代表不同的归纳偏置,即对数据底层结构的假设。选择不同的度量方式将影响模型的泛化能力。
神经网络的“非参数性”¶
神经网络的特点是过度参数化(over-parameterized),即拥有远多于训练数据所需的参数。由于过度参数化,神经网络在训练数据上常常能够完美拟合(interpolate),这种行为与非参数模型相似。
深度学习的最新理论研究表明,大型神经网络与非参数方法,特别是核方法(kernel methods),之间有深刻的联系。
具体来说,神经切线核(neural tangent kernel)理论表明,当多层感知机(MLP)的宽度趋于无穷大时,它们的行为趋近于非参数的核方法。
神经切线核理论¶
神经切线核(neural tangent kernel,NTK)是一种特殊的核函数,用来描述深度神经网络的行为。
尽管当前的NTK模型可能不能完全解释现代深度网络的行为,但它为分析过度参数化的深度神经网络提供了有力的工具,并强调了非参数建模在理解深度网络行为中的重要性。
结论¶
通过对比传统的参数化和非参数化模型,强调了神经网络在某些方面表现得像非参数模型。
尽管神经网络有大量参数,但其过度参数化的特性使其在训练数据上的拟合方式与非参数方法类似,尤其是在训练数据量增大时。通过神经切线核的理论,研究表明神经网络与核方法之间有着深刻的联系,这一理论为理解现代深度学习模型提供了新的视角。
5.5.3. Early Stopping¶
本文探讨了 早停法(Early Stopping) 在深度学习中的作用及其在处理标签噪声(label noise)问题上的重要性。
早停法的动机与背景¶
深度神经网络具备拟合任意标签的能力,即使标签是随机分配或错误的。然而,这种拟合能力通常需要多次训练迭代后才会显现。
研究发现,神经网络在训练过程中,首先拟合干净的标签数据,随后逐步拟合带噪声的标签数据。这意味着,如果训练在模型拟合干净数据后停止,模型仍能保持良好的泛化能力。
当模型只拟合干净数据,而未完全拟合随机标签时,实际上可以确保模型具备良好的泛化能力。
早停法的机制¶
早停法是一种经典的正则化技术,与直接约束权重值不同,它通过 限制训练的迭代次数(epoch) 来防止模型过拟合。
早停的典型方法是监控验证集误差,在训练过程中,每个epoch结束后评估一次验证集误差。当验证误差在连续多个epoch内未显著减少(减少幅度小于
早停法的优点¶
提高泛化能力:特别是在标签存在噪声或标签固有不确定性的场景下,早停能防止模型过度拟合带噪声数据,进而提升泛化能力。
节约计算资源:早停可以显著减少训练时间。对于大型模型(如GPT等),训练可能需要数天且消耗大量GPU资源,早停能够节省大量计算成本。
适用场景¶
标签存在噪声或不确定性:例如医疗领域的死亡率预测,患者数据通常带有不确定性和噪声,早停尤为关键。
真实可分数据集(realizable datasets):例如区分猫和狗的任务,如果数据集无标签噪声且类别完全可分,早停对泛化能力的提升 不显著 。
错误做法:如果继续训练直到模型完全拟合带噪声的数据,通常会导致模型泛化能力下降,表现出较高的测试误差。
关键词解析¶
Label Noise(标签噪声):训练数据中存在错误或随机分配的标签,常见于真实世界的数据集中。
Generalization(泛化):模型在未见过的新数据上的表现能力。
Patience Criterion(耐心准则):在验证误差多次不降低后停止训练的策略,用于防止模型在带噪声数据上继续拟合。
结论¶
早停法是应对深度学习中过拟合问题的重要手段,尤其在标签噪声存在的情况下,它能够有效提升模型的泛化能力,同时降低训练时间和成本。
虽然在理想、无噪声的数据集上效果有限,但在现实中,标签噪声和数据的不确定性使得早停法成为深度学习训练的常见技巧之一。
5.5.4. Classical Regularization Methods for Deep Networks¶
本节探讨了深度学习中的经典正则化方法,主要围绕 权重衰减(weight decay) 和正则化技术在防止过拟合中的作用和局限性。
经典正则化方法的回顾¶
在传统机器学习中,正则化通过在损失函数中添加惩罚项来限制模型复杂度,从而防止过拟合。
- 主要方法包括:
岭回归(ridge regularization):惩罚
套索回归(lasso regularization):惩罚
这些方法通常足够强大,可以防止模型拟合随机标签(即防止模型学到噪声)。
深度学习中的应用与挑战¶
- 在深度学习中,权重衰减依然是流行的正则化工具。然而,研究表明:
典型的
换句话说,单独依靠权重衰减可能无法有效抑制过拟合。
其真正的价值可能体现在与 早停法(early stopping) 的组合使用中,形成双重正则化策略。
对正则化方法的新解释¶
在深度学习中,正则化方法的作用可能与传统理论不同。
即使正则化不能直接限制模型的拟合能力,它可能通过引入**归纳偏置(inductive biases)**来促进模型对数据内在模式的学习。
类比于k近邻算法中距离度量的选择,不同的正则化方法可能更多地是通过改变模型的学习方式,而非显著限制模型复杂度来提升泛化能力。
正则化方法的扩展与创新¶
- 深度学习研究者不仅继续使用传统正则化方法,还基于这些方法发展了新的技术,如:
在模型输入上添加噪声:这可以在训练过程中增加模型的鲁棒性,减少对训练数据的过度依赖。
Dropout:通过随机丢弃一部分神经元的输出,防止神经网络对特定路径过度依赖,是深度学习中最流行的正则化方法之一。
即使dropout的理论基础尚不完全清晰,它在实践中的有效性已被广泛验证。
关键词解析¶
Weight Decay(权重衰减):通过在损失函数中添加
Inductive Bias(归纳偏置):模型在学习过程中表现出的倾向性或假设,有助于模型更好地理解数据分布。
Dropout:训练过程中随机丢弃神经元输出,减少神经元之间的共适应性,降低过拟合风险。
结论¶
这段文字强调了深度学习对经典正则化方法的借鉴和创新。
尽管传统正则化方法如权重衰减仍然广泛使用,但在深度学习中,它们的作用机制可能更复杂,且往往需要与其他策略(如早停法)结合使用。
未来,探索这些正则化方法背后的理论基础,将是理解深度学习泛化能力的重要方向。
5.6. Dropout¶
这部分介绍了Dropout,一种在训练神经网络时防止过拟合的正则化技术。
为什么需要Dropout:
简化模型是提高泛化能力的核心思路之一: 减少模型参数的维度。 使用权重衰减(L2正则化),限制参数的大小。 提高模型的平滑性,使模型对输入的小扰动不敏感。 直观解释:在图像分类任务中,如果输入图像的像素增加了一些随机噪声,模型仍应给出相同的分类结果。Dropout的提出:
Dropout 源自Bishop提出的一个理论: 在输入中加入随机噪声,相当于Tikhonov正则化,可以提高模型对输入扰动的鲁棒性。 Srivastava等人将这一思想推广到网络的内部层,提出了Dropout方法。 Dropout的核心思想: 在每次前向传播时,随机“丢弃”一部分神经元,即将它们的输出置零。 训练过程中,每次迭代都会对不同的神经元进行随机屏蔽。 这种方法打破了神经网络中过度依赖特定激活模式的问题,防止神经元之间形成共适应(co-adaptation)。 作者将其类比于生物的有性繁殖打破基因共适应的过程。Dropout的实现:
在前向传播中,神经元以概率$p$被丢弃(置零),其余神经元以概率$1-p$保留。 为了保持输出期望不变,保留的神经元的输出被除以$(1-p)$进行缩放。
公式:
其中
h是原始激活值h'是Dropout后的激活值这样设计的目的是确保期望不变
小结:
Dropout是一种简单而有效的正则化方法,在大多数深度学习框架中已成为标准做法。
它可以有效地减少过拟合,使模型对输入数据的微小扰动更加鲁棒。
Dropout打破了神经元之间的共适应关系,提高了模型的泛化能力。
5.6.1. Dropout in Practice¶
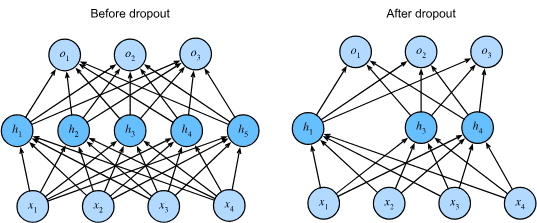
Fig. 5.6.1 MLP before and after dropout.
5.6.2. Implementation from Scratch¶
实现了一个 dropout_layer 函数,该函数以 dropout 概率丢弃张量输入 X 中的元素,并按上述方式重新调整余数:除以 1.0-dropout 的幸存者:
def dropout_layer(X, dropout): assert 0 <= dropout <= 1 if dropout == 1: return torch.zeros_like(X) mask = (torch.rand(X.shape) > dropout).float() return mask * X / (1.0 - dropout)
将输入 X 通过 dropout 操作传递,概率分别为 0、0.5 和 1:
X = torch.arange(16, dtype = torch.float32).reshape((2, 8))
print('dropout_p = 0:', dropout_layer(X, 0))
print('dropout_p = 0.5:', dropout_layer(X, 0.5))
print('dropout_p = 1:', dropout_layer(X, 1))
# 输出
# dropout_p = 0: tensor([[ 0., 1., 2., 3., 4., 5., 6., 7.],
# [ 8., 9., 10., 11., 12., 13., 14., 15.]])
# dropout_p = 0.5: tensor([[ 0., 2., 0., 6., 8., 0., 0., 0.],
# [16., 18., 20., 22., 24., 26., 28., 30.]])
# dropout_p = 1: tensor([[0., 0., 0., 0., 0., 0., 0., 0.],
# [0., 0., 0., 0., 0., 0., 0., 0.]])
5.6.2.1. Defining the Model¶
下面的模型将 dropout 应用于每个隐藏层的输出(在激活函数之后):
class DropoutMLPScratch(d2l.Classifier):
def __init__(self, num_outputs, num_hiddens_1, num_hiddens_2,
dropout_1, dropout_2, lr):
super().__init__()
self.save_hyperparameters()
self.lin1 = nn.LazyLinear(num_hiddens_1)
self.lin2 = nn.LazyLinear(num_hiddens_2)
self.lin3 = nn.LazyLinear(num_outputs)
self.relu = nn.ReLU()
def forward(self, X):
H1 = self.relu(self.lin1(X.reshape((X.shape[0], -1))))
if self.training:
H1 = dropout_layer(H1, self.dropout_1)
H2 = self.relu(self.lin2(H1))
if self.training:
H2 = dropout_layer(H2, self.dropout_2)
return self.lin3(H2)
5.6.2.2. Training¶
hparams = {'num_outputs':10, 'num_hiddens_1':256, 'num_hiddens_2':256,
'dropout_1':0.5, 'dropout_2':0.5, 'lr':0.1}
model = DropoutMLPScratch(**hparams)
data = d2l.FashionMNIST(batch_size=256)
trainer = d2l.Trainer(max_epochs=10)
trainer.fit(model, data)
5.6.3. Concise Implementation¶
在每个全连接层之后添加一个 Dropout 层,将 dropout 概率作为唯一参数传递给其构造函数
在训练过程中, Dropout 层将根据指定的丢弃概率随机丢弃前一层的输出(或等效地,后续层的输入)。
当不处于训练模式时, Dropout 层仅在测试期间传递数据。
class DropoutMLP(d2l.Classifier):
def __init__(self, num_outputs, num_hiddens_1, num_hiddens_2,
dropout_1, dropout_2, lr):
super().__init__()
self.save_hyperparameters()
self.net = nn.Sequential(
nn.Flatten(), nn.LazyLinear(num_hiddens_1), nn.ReLU(),
nn.Dropout(dropout_1), nn.LazyLinear(num_hiddens_2), nn.ReLU(),
nn.Dropout(dropout_2), nn.LazyLinear(num_outputs))
训练模型:
model = DropoutMLP(**hparams)
trainer.fit(model, data)
5.6.4. Summary¶
除了控制维数和权重向量的大小之外,dropout 是避免过度拟合的另一种工具。
通常,工具是联合使用的。
请注意,dropout 仅在训练期间使用:它将激活 h 替换为具有预期值 h 的随机变量
5.7. Predicting House Prices on Kaggle¶
以一个 Kaggle 上的示例进行讲解
Part 2: Modern Deep Learning Techniques¶
6. Builders’ Guide¶
除了庞大的数据集和强大的硬件之外,还有出色的软件工具 在深度学习的快速进展中发挥了不可或缺的作用 学习。
在本章中,我们将深入挖掘深度学习计算的关键组成部分,即模型构建、参数访问和初始化、设计自定义层和块、将模型读写到磁盘,以及利用 GPU 实现梦幻般的加速。
虽然本章没有介绍任何新模型或数据集,但接下来的高级建模章节在很大程度上依赖于这些技术。
6.1. Layers and Modules¶
Individual layers can be modules.
Many layers can comprise a module.
Many modules can comprise a module.
6.2. Parameter Management¶
示例:
net = nn.Sequential(nn.LazyLinear(8),
nn.ReLU(),
nn.LazyLinear(1))
X = torch.rand(size=(2, 4))
net(X).shape
# torch.Size([2, 1])
6.2.1. Parameter Access¶
检查第二个全连接层的参数:
# 执行 net(X) 前
$ net[2].state_dict()
# OrderedDict([('weight', <UninitializedParameter>),
('bias', <UninitializedParameter>)])
# 执行 net(X) 后
$ net[2].state_dict()
# OrderedDict([('weight',
tensor([[-0.1649, 0.0605, 0.1694, -0.2524, 0.3526, -0.3414, -0.2322, 0.0822]])),
('bias', tensor([0.0709]))])
6.2.1.1. Targeted Parameters¶
从第二个神经网络层提取偏差,该层返回参数类实例,并进一步访问该参数的值:
$ type(net[2].bias), net[2].bias.data
# (torch.nn.parameter.Parameter, tensor([0.0709]))
$ net[2].weight
Parameter containing:
tensor([[ 0.0205, -0.1554, -0.2950, 0.1296, -0.2784, 0.1173, -0.0230, -0.1530]],
requires_grad=True)
备注
参数是复杂的对象,包含值、梯度和附加信息。
6.2.1.2. All Parameters at Once¶
$ [(name, param.shape) for name, param in net.named_parameters()]
# [('0.weight', torch.Size([8, 4])),
('0.bias', torch.Size([8])),
('2.weight', torch.Size([1, 8])),
('2.bias', torch.Size([1]))]
6.2.2. Tied Parameters¶
跨多个层共享参数:
# We need to give the shared layer a name so that we can refer to its parameters
shared = nn.LazyLinear(8)
net = nn.Sequential(nn.LazyLinear(8), nn.ReLU(),
shared, nn.ReLU(),
shared, nn.ReLU(),
nn.LazyLinear(1))
net(X)
# Check whether the parameters are the same
print(net[2].weight.data[0] == net[4].weight.data[0])
net[2].weight.data[0, 0] = 100
# Make sure that they are actually the same object rather than just having the
# same value
print(net[2].weight.data[0] == net[4].weight.data[0])
# 输出
# tensor([True, True, True, True, True, True, True, True])
# tensor([True, True, True, True, True, True, True, True])
备注
由于模型参数包含梯度,因此在反向传播时将第二隐藏层和第三隐藏层的梯度相加。
6.3. Parameter Initialization¶
使用内置和自定义初始化程序来初始化参数。
示例:
net = nn.Sequential(nn.LazyLinear(8), nn.ReLU(), nn.LazyLinear(1))
X = torch.rand(size=(2, 4))
net(X).shape
6.3.1. Built-in Initialization¶
初使状态:
net[0].weight.data[0], net[0].bias.data[0]
# Out[27]: (tensor([ 0.4112, -0.0801, 0.4687, 0.3344]), tensor(-0.1189))
示例1-将所有权重参数初始化为标准差为 0.01 的高斯随机变量,而偏差参数则清除为零:
def init_normal(module):
if type(module) == nn.Linear:
nn.init.normal_(module.weight, mean=0, std=0.01)
nn.init.zeros_(module.bias)
net.apply(init_normal)
net[0].weight.data[0], net[0].bias.data[0]
# 输出
# (tensor([-0.0082, 0.0074, 0.0116, -0.0061]), tensor(0.))
示例2-将所有参数初始化为给定的常量值(例如 1):
def init_constant(module):
if type(module) == nn.Linear:
nn.init.constant_(module.weight, 1)
nn.init.zeros_(module.bias)
net.apply(init_constant)
net[0].weight.data[0], net[0].bias.data[0]
# 输出
(tensor([1., 1., 1., 1.]), tensor(0.))
示例3-为某些块应用不同的初始化器。例如,下面我们使用 Xavier 初始化器初始化第一层,并将第二层初始化为常量值 42:
def init_xavier(module):
if type(module) == nn.Linear:
nn.init.xavier_uniform_(module.weight)
def init_42(module):
if type(module) == nn.Linear:
nn.init.constant_(module.weight, 42)
net[0].apply(init_xavier)
net[2].apply(init_42)
print(net[0].weight.data[0])
print(net[2].weight.data)
# 输出
tensor([-0.0974, 0.1707, 0.5840, -0.5032])
tensor([[42., 42., 42., 42., 42., 42., 42., 42.]])
6.4. Lazy Initialization¶
延迟初始化很方便,允许框架自动推断参数形状,从而可以轻松修改架构并消除一种常见的错误源。我们可以通过模型传递数据来让框架最终初始化参数。
实例化一个 MLP:
net = nn.Sequential(nn.LazyLinear(256), nn.ReLU(), nn.LazyLinear(10))
尝试访问以下参数进行确认:
net[0].weight
# 输出
<UninitializedParameter>
通过网络传递数据,让框架最终初始化参数:
X = torch.rand(2, 20)
net(X)
一旦知道所有参数形状,框架就可以最终初始化参数:
net[0].weight.shape
# 输出
torch.Size([256, 20])
6.5. Custom Layers¶
通过基本图层类来设计自定义图层。
这使我们能够定义灵活的新层,其行为与库中任何现有层不同。一旦定义,自定义层就可以在任意上下文和架构中调用。层可以具有本地参数,可以通过内置函数创建这些参数。
6.5.1. Layers without Parameters¶
class CenteredLayer(nn.Module):
def __init__(self):
super().__init__()
def forward(self, X):
return X - X.mean()
使用:
layer = CenteredLayer()
layer(torch.tensor([1.0, 2, 3, 4, 5]))
# 输出
tensor([-2., -1., 0., 1., 2.])
incorporate our layer as a component in constructing more complex models:
net = nn.Sequential(nn.LazyLinear(128), CenteredLayer())
使用:
Y = net(torch.rand(4, 8))
Y.mean()
6.5.2. Layers with Parameters¶
具有可通过训练调整的参数的层:
class MyLinear(nn.Module):
def __init__(self, in_units, units):
super().__init__()
self.weight = nn.Parameter(torch.randn(in_units, units))
self.bias = nn.Parameter(torch.randn(units,))
def forward(self, X):
linear = torch.matmul(X, self.weight.data) + self.bias.data
return F.relu(linear)
6.6. File I/O¶
6.6.1. Loading and Saving Tensors¶
对于单个张量,我们可以直接调用load和save 分别读取和写入它们的函数:
x = torch.arange(4)
torch.save(x, 'x-file')
x2 = torch.load('x-file')
x2
# 输出
tensor([0, 1, 2, 3])
存储张量列表并将它们读回内存:
y = torch.zeros(4)
torch.save([x, y],'x-files')
x2, y2 = torch.load('x-files')
(x2, y2)
编写和读取从字符串映射到张量的字典:
mydict = {'x': x, 'y': y}
torch.save(mydict, 'mydict')
mydict2 = torch.load('mydict')
mydict2
6.6.2. Loading and Saving Model Parameters¶
模型示例:
class MLP(nn.Module):
def __init__(self):
super().__init__()
self.hidden = nn.LazyLinear(256)
self.output = nn.LazyLinear(10)
def forward(self, x):
return self.output(F.relu(self.hidden(x)))
net = MLP()
X = torch.randn(size=(2, 20))
Y = net(X)
将模型的参数存储为名为“mlp.params”的文件:
torch.save(net.state_dict(), 'mlp.params')
恢复模型:
clone = MLP()
clone.load_state_dict(torch.load('mlp.params'))
clone.eval()
# 输出
MLP(
(hidden): LazyLinear(in_features=0, out_features=256, bias=True)
(output): LazyLinear(in_features=0, out_features=10, bias=True)
)
备注
可以通过参数字典保存和加载网络的整套参数。保存架构必须通过代码而不是参数来完成。
6.7. GPUs¶
备注
要运行本节中的程序,您至少需要两个 GPU。
6.7.1. Computing Devices¶
指定用于存储和计算的设备:
def cpu(): #@save
"""Get the CPU device."""
return torch.device('cpu')
def gpu(i=0): #@save
"""Get a GPU device."""
return torch.device(f'cuda:{i}')
cpu(), gpu(), gpu(1)
# 输出
(device(type='cpu'),
device(type='cuda', index=0),
device(type='cuda', index=1))
查询可用GPU的数量:
def num_gpus(): #@save
"""Get the number of available GPUs."""
return torch.cuda.device_count()
num_gpus()
工具(GPU不存在则使用CPU):
def try_gpu(i=0): #@save
"""Return gpu(i) if exists, otherwise return cpu()."""
if num_gpus() >= i + 1:
return gpu(i)
return cpu()
def try_all_gpus(): #@save
"""Return all available GPUs, or [cpu(),] if no GPU exists."""
return [gpu(i) for i in range(num_gpus())]
try_gpu(), try_gpu(10), try_all_gpus()
6.7.2. Tensors and GPUs¶
6.7.2.1. Storage on the GPU¶
使用第一个GPU:
X = torch.ones(2, 3, device=try_gpu())
X
# 输出
tensor([[1., 1., 1.],
[1., 1., 1.]], device='cuda:0')
如果有两个GPU:
Y = torch.rand(2, 3, device=try_gpu(1))
Y
# 输出
tensor([[0.0022, 0.5723, 0.2890],
[0.1456, 0.3537, 0.7359]], device='cuda:1')
6.7.2.2. Copying¶
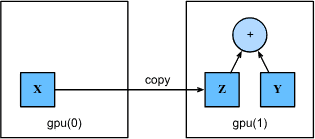
Fig. 6.7.1 Copy data to perform an operation on the same device.¶
由于 Y 位于第二个 GPU 上,因此我们需要将 X 移动到那里,然后才能将两者相加:
Z = X.cuda(1)
print(X)
print(Z)
# 输出
tensor([[1., 1., 1.],
[1., 1., 1.]], device='cuda:0')
tensor([[1., 1., 1.],
[1., 1., 1.]], device='cuda:1')
现在数据( Z 和 Y )都在同一个 GPU 上:
Y + Z
# 输出
tensor([[1.0022, 1.5723, 1.2890],
[1.1456, 1.3537, 1.7359]], device='cuda:1')
6.7.3. Neural Networks and GPUs¶
神经网络模型可以指定设备。以下代码将模型参数放在 GPU 上:
net = nn.Sequential(nn.LazyLinear(1))
net = net.to(device=try_gpu())
Let the trainer support GPU:
@d2l.add_to_class(d2l.Trainer) #@save
def __init__(self, max_epochs, num_gpus=0, gradient_clip_val=0):
self.save_hyperparameters()
self.gpus = [d2l.gpu(i) for i in range(min(num_gpus, d2l.num_gpus()))]
@d2l.add_to_class(d2l.Trainer) #@save
def prepare_batch(self, batch):
if self.gpus:
batch = [a.to(self.gpus[0]) for a in batch]
return batch
@d2l.add_to_class(d2l.Trainer) #@save
def prepare_model(self, model):
model.trainer = self
model.board.xlim = [0, self.max_epochs]
if self.gpus:
model.to(self.gpus[0])
self.model = model
6.7.4. Summary¶
默认情况下,数据在主存中创建,然后使用CPU进行计算。
深度学习框架要求计算的所有输入数据都位于同一设备上,无论是CPU还是同一个GPU。
如果不小心移动数据,您可能会损失显着的性能。
备注
一个典型的错误如下:计算 GPU 上每个小批量的损失并在命令行上将其报告给用户(或将其记录在 NumPy ndarray 中)将触发全局解释器锁定,该锁定会停止所有 GPU。最好在 GPU 内部分配内存用于日志记录,并且只移动较大的日志。
跨设备传输数据会导致性能损失。比如,数据从 CPU 传到 GPU,或者在多个 GPU 之间频繁传输,都会增加开销。关键点是: 尽量避免不必要的数据传输,尤其是小批量数据的频繁移动。
错误示例:在 GPU 上计算每个小批量(minibatch)的损失(loss),然后将其传回 CPU 并转换为 NumPy 数组进行记录或显示。 问题:这种方式会触发全局解释器锁(Global Interpreter Lock,GIL),导致 GPU 暂停,等待 CPU 完成操作,从而降低计算效率。
优化建议:最佳做法是直接在 GPU 上分配内存记录日志,减少数据在 CPU 和 GPU 之间频繁移动。等日志累积到足够大的批次时,再将其移动到 CPU 进行后续处理或显示。
7. Convolutional Neural Networks¶
7.1. From Fully Connected Layers to Convolutions¶
7.1.1. Invariance(不变性)¶
解释 CNN 如何通过平移不变性和局部性来减少模型复杂度,提高对图像中物体位置的鲁棒性(即使位置变化也能识别)。
CNN 通过模拟人类视觉的逐层处理方式,能够有效学习图像特征,并在不同位置进行一致识别。
定义¶
目标:识别图像中的对象时,希望模型对对象在图像中的具体位置不敏感。
核心思想是:识别一个对象时,关注对象的特征,而不是其位置。
比如,无论一只猪出现在图像顶部还是底部,我们都应该能够识别出它是一只猪。这种位置不敏感性就是不变性(invariance)。
CNN 如何实现这种不变性¶
- (1)平移不变性(Translation Invariance):
无论图像的某个局部区域(patch)出现在什么位置,网络都应该对它有相似的响应。
卷积层通过在图像上滑动一个滤波器(kernel)来实现这一点,即使物体的位置发生变化,滤波器依然可以检测到它。
例子:在一张猫的图片中,滤波器在猫的耳朵上或猫的爪子上滑动时,都会产生相应的激活,从而检测到猫的存在。
- (2)局部性原则(Locality):
在网络的前几层,卷积操作主要关注局部区域(local region),而不考虑图像中远处的内容。
这种方法模拟了人类视觉系统中对局部特征(如边缘、角等)的关注。
意义:每次只处理一小部分图像,有助于减少计算量,并捕捉基本特征。最终,通过不断堆叠卷积层和池化层,模型可以聚合这些局部特征,形成对整个图像的理解。
- (3)深层特征提取:
随着网络逐渐加深,感受野(receptive field)变大,网络可以学习到更长距离的特征关系,类似于更高级别的视觉感知。
这种方式使得 CNN 能够捕捉更复杂、更抽象的图像特征。
例子:在浅层,网络可能学习到边缘和纹理等简单特征,而在更深的层中,网络可能学习到眼睛、鼻子等复杂特征,最终能够识别出整个脸部。
7.1.2. Constraining the MLP¶
整体¶
本节探讨的是如何将多层感知机(MLP)应用到二维图像上,并分析了这样做带来的挑战和参数爆炸问题。
在传统的 MLP 中,输入是一个扁平的向量,但对于图像来说,我们希望保留空间结构(spatial structure),即图像的二维形状。
理解 MLP 对二维图像的建模¶
假设输入图像
权重矩阵到权重张量的切换¶
传统 MLP:在传统 MLP 中,隐藏层的每个神经元与输入层的所有像素相连,连接权重用一个二维矩阵
- 二维图像 MLP:
如果将每个隐藏单元都连接到输入图像的所有像素,我们需要一个四阶权重张量
这个四阶张量表示从输入图像位置 (k,l) 到隐藏层位置 (i,j) 的权重。
公式解释:
位置 (i,j) 处的隐藏单元
卷积的引入与参数重索引¶
为了减少复杂度,我们引入卷积的思想,将权重矩阵
这里的
权重索引变化:
这个索引变换意味着:卷积核以 (i,j) 为中心,采样相邻偏移量 (a,b) 处的像素。
参数量爆炸问题¶
假设输入图像大小为
如果每个像素都与所有像素相连,权重张量
这种参数量远远超出了计算机的处理能力。
问题的根源与解决思路¶
问题根源: MLP 的全连接结构使每个隐藏单元都与所有输入像素相连,导致参数量爆炸。
- 解决方法:
局部感受野(local receptive field): 仅让隐藏单元与输入图像的局部区域相连,而非整个图像。
共享权重: 通过卷积层的方式,减少参数数量并增强平移不变性。
池化层(pooling): 进一步降低分辨率,减少计算量。
小结¶
核心思想是:直接将 MLP 应用于高维图像会导致参数量巨大,不具备实际可行性。
通过引入卷积的概念,限制感受野范围,可以有效减少参数量,并保持对图像空间结构的敏感性。
这种方法构成了卷积神经网络(CNN)的基础,极大提升了模型的计算效率和识别能力。
7.1.2.1. Translation Invariance¶
平移不变性(Translation Invariance):
定义: 平移不变性意味着:如果输入图像发生平移,隐藏层的输出也应发生同样的平移,而不会改变特征本身的性质。
直观理解: 如果在图像的不同位置看到相同的特征(如边缘或角),网络应当能识别它,而不在意特征的具体位置。
数学解释¶
原始表示方式中,权重
引入平移不变性后: 权重只与相对偏移量 (a,b) 有关,不再依赖具体位置:
偏置
left[mathbf{H}right]_{i, j} &= u + sum_a sum_b [mathsf{V}]_{a, b} [mathbf{X}]_{i+a, j+b}
7.1.2.2. Locality¶
局部感受野(Locality)
定义: 局部感受野意味着:隐藏层的每个神经元只关注输入图像的局部区域,而非整个图像。
动机: 在图像中,远离当前像素的区域对理解该位置像素的影响较小。因此,感受野可以限制在较小范围内。
实现方式: 在距离超过
公式表示:
引入局部感受野后,卷积核尺寸从
这将参数量进一步减少到:
结果: 参数量减少了四个数量级,使得卷积层更加高效。
总结与启示¶
卷积核的作用: 提取图像局部特征,减少参数量,提升网络对图像的空间敏感性。
平移不变性的代价: 卷积核只能感知局部特征,在处理全局信息时需要更深的网络结构(更多层的卷积+池化)。
深层网络: 通过堆叠多层卷积层,可以逐层捕获更复杂、更抽象的特征,实现对整幅图像的理解。
直观类比:可以把 CNN 的卷积核想象成放大镜或探测器,它在图像中移动,寻找感兴趣的特征。通过限制探测器的大小和移动范围,我们既减少了复杂度,又提高了模型的效率和泛化能力。
CNN的优势¶
参数高效: CNN 只需少量参数即可处理高分辨率图像。
鲁棒性强: CNN 对图像的平移和局部变化具有较强的鲁棒性,能够更好地泛化到新数据。
特征层次化: 通过多层卷积,可以逐步学习低级(如边缘)到高级(如物体)特征。
计算高效: 卷积操作易于并行计算,适合 GPU 加速。
7.1.3. Convolutions¶
定义¶
卷积是信号处理和图像处理中常用的数学操作。
本质上,它是一种滑动窗口操作,计算两个函数或矩阵的重叠程度。
卷积的关键在于一个函数或矩阵在另一个函数或矩阵上进行滑动,并计算在每个位置上的重叠量。
数学定义¶
连续卷积公式¶
- 解释
f(z):原始信号或图像。
𝑔(𝑥−𝑧):滤波器 (或核函数) 在位置 𝑥 处翻转后平移的结果。
积分表示对所有可能的重叠进行累加。
- 直观理解:
类似将一个图形 𝑔 翻转后,在图形 𝑓 上逐个位置滑动,计算重叠区域的面积。
每个滑动位置都生成一个数值,表示该位置的匹配程度。
离散卷积公式(一维)¶
在离散场景下,积分变为求和。滑动窗口在每个位置 𝑖 上计算 𝑓 和 𝑔 的内积。
二维卷积公式¶
二维卷积扩展了概念,在 𝑎,𝑏 方向滑动滤波器,计算二维图像与滤波器的重叠程度。
卷积和交叉相关的区别¶
- 交叉相关 (Cross-correlation):
滤波器 𝑔 在滑动时不进行翻转,直接平移和累加。
卷积核和原始图像在相同方向滑动。
- 卷积 (Convolution):
卷积的滤波器 𝑔(𝑖−𝑎,𝑗−𝑏) 是翻转后的版本。
实际深度学习中,通常使用交叉相关的形式,称之为“卷积”。
- 为什么使用交叉相关?
计算效率高,结果相似。
翻转操作在实现中可忽略,因此深度学习框架默认使用交叉相关。
卷积的实际意义¶
- 卷积可在图像中提取局部特征,例如:
检测边缘、角点、纹理等。
在不同层中逐渐捕捉更复杂的模式,从低级特征 (边缘) 到高级特征 (物体轮廓或类别)。
卷积是构建卷积神经网络 (CNN) 的核心操作
7.1.4. Channels¶
1. 图像的多通道特性¶
实际图像通常有 三通道:红 (R)、绿 (G)、蓝 (B)。
每个像素点不仅包含一个灰度值,而是一个向量,表示不同颜色的组合。
因此,图像是三阶张量 1024×1024×3,表示高度、宽度和通道数。
2. 为什么需要多通道卷积¶
简单的二维卷积只能处理灰度图像。
- 多通道卷积可以:
处理复杂的彩色图像。
在每个通道上分别提取特征,最终结合生成更丰富的特征表达。
允许不同滤波器学习捕捉图像的不同方面,例如边缘、纹理和颜色分布。
3. 数学定义¶
多通道卷积公式:
i,j:表示卷积在图像上的空间位置。
𝑐:输入通道索引。
𝑑:输出通道索引 (不同滤波器产生不同的输出通道)。
核 𝑉 是一个四阶张量,维度为 𝑎,𝑏,𝑐,𝑑,即滤波器大小和输入输出通道数。
4. 直观理解¶
将滤波器在每个通道上分别滑动,然后在所有通道上的结果相加,得到最终的输出特征。
这种方式类似于对图像的不同部分进行特征组合,生成更加复杂的表达。
5. 隐藏表示和特征图 (Feature Maps)¶
每个卷积层的输出也是多通道的,即隐藏表示 𝐻 也是三阶张量。
- 每个隐藏通道捕捉不同类型的特征。例如:
第一个通道检测边缘。
第二个通道检测角点。
第三个通道检测纹理或复杂形状。
这些输出通道常称为“特征图”或“特征通道”。
6. 多层卷积的特征提取机制¶
低层卷积层: 提取简单特征 (如边缘)。
中层卷积层: 组合低层特征,提取更复杂的形状或结构。
高层卷积层: 识别物体或场景中的高级特征,如人脸或特定物体。
7. 通道的现实意义¶
多通道卷积帮助模型捕捉更复杂的视觉特征,提高模型表达能力。
深度卷积网络 (CNN) 在图像分类、目标检测和分割等任务中表现卓越,部分原因在于多通道卷积的强大能力。
8. 关键点总结¶
通道允许卷积层处理彩色图像或多维特征,使CNN在实际应用中表现更强大。
多通道输出表示不同层次的特征组合,为网络提供更全面的图像表示能力。
7.1.5. Summary and Discussion¶
关键点¶
平移不变性 (Translation Invariance):图像中的物体无论出现在图像的哪个位置,卷积操作都能以相同的方式处理它。这种不变性是 CNN 设计的重要原则之一。
局部性 (Locality):每个卷积核仅关注图像的小区域 (局部感受野),并通过滑动窗口机制逐个位置计算特征,逐步构建全局理解。
理解¶
解释:CNN 的核心优势在于能够高效地提取局部特征,并保持对位置信息的不敏感性,这种设计使 CNN 适用于图像分类、目标检测等任务。
类比:想象一个人观察一张图片时,通常不会一次性关注整张图像,而是逐个区域观察并理解细节。这种局部关注和逐步汇总的方式与 CNN 的工作方式相似。
降低复杂度与参数数量¶
问题:大规模图像或高维数据通常具有极高的维度,直接建模计算量巨大且参数过多,容易导致模型过拟合或计算不可行。
解决方案:CNN 通过卷积操作,强制模型只关注局部区域,减少参数数量,同时保留足够的表达能力。这种策略将复杂的计算问题转化为可行的模型,避免了计算和统计上的不可行性。
示例:假设原始图像大小为 1024×1024×3,如果直接使用全连接层,参数量非常庞大。而卷积核通常大小为 3×3 或 5×5,参数数量显著减少。
理解要点:降维和特征提取的同时不丢失关键信息,是 CNN 在高效处理复杂数据时的重要特性。
引入通道 (Channels) 增强模型能力¶
背景:卷积核的局部性和平移不变性在降低复杂度的同时,也限制了模型的表达能力。
解决方法:引入多个通道 (如 RGB),允许模型学习更复杂和多样的特征,弥补了局部卷积带来的表达能力损失。
- 进一步扩展:图像中常见的三个通道 (红、绿、蓝),是基本的颜色信息。然而,实际应用中可能存在更多通道。例如:
卫星图像: 可能包含几十甚至上百个通道 (多光谱或高光谱图像),记录不同波长的反射数据。
医学成像: MRI 或 CT 扫描中不同通道可能代表不同的层面或组织特性。
理解:通过引入额外通道,CNN 可以处理更复杂的数据,学习多维度的特征表示,从而提升模型的表现力和泛化能力。
7.2. Convolutions for Images¶
7.2.1. The Cross-Correlation Operation¶
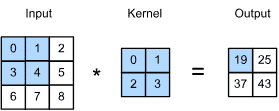
输入是一个高度为3、宽度为3的二维张量。我们将张量的形状标记为 3x3 或 (3,3)。kernel的高度和宽度都是2。kernel window (or convolution window)的形状由内核的高度和宽度给出(这里是 2x2 )。¶
在二维互相关运算(two-dimensional cross-correlation operation)中,我们从位于输入张量左上角的卷积窗口开始,并将其从左到右、从上到下滑动穿过输入张量。
当卷积窗口滑动到某个位置时,该窗口中包含的输入子张量与内核张量按元素相乘,并将所得张量相加,生成单个标量值。
该结果给出了相应位置处的输出张量的值。
输出大小由输入大小
代码:
def corr2d(X, K): #@save
"""Compute 2D cross-correlation."""
h, w = K.shape
Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
return Y
X = torch.tensor([[0.0, 1.0, 2.0],
[3.0, 4.0, 5.0],
[6.0, 7.0, 8.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
corr2d(X, K)
# 输出
tensor([[19., 25.],
[37., 43.]])
7.2.2. Convolutional Layers¶
前向传播方法:
class Conv2D(nn.Module):
def __init__(self, kernel_size):
super().__init__()
self.weight = nn.Parameter(torch.rand(kernel_size))
self.bias = nn.Parameter(torch.zeros(1))
def forward(self, x):
return corr2d(x, self.weight) + self.bias
7.2.3. Object Edge Detection in Images¶
构建一个 6x8 像素的“图像”。中间四列是黑色( 0 ),其余是白色( 1 ):
X = torch.ones((6, 8))
X[:, 2:6] = 0
X
# 输出
tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.]])
构造一个高度为1、宽度为2的 kernel K
此内核是有限差分运算符的特例: At location
代码实现:
K = torch.tensor([[1.0, -1.0]])
参数 X (我们的 input) 和 K (我们的 kernel) 执行 cross-correlation operation:
Y = corr2d(X, K)
Y
# 输出
tensor([[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.]])
将内核应用于转置图像。正如预期的那样,它消失了。内核 K 仅检测垂直边缘:
corr2d(X.t(), K)
# 输出
tensor([[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]])
7.2.4. Learning a Kernel¶
# Construct a two-dimensional convolutional layer with 1 output channel and a kernel of shape (1, 2).
# For the sake of simplicity, we ignore the bias here
conv2d = nn.LazyConv2d(1, kernel_size=(1, 2), bias=False)
# The two-dimensional convolutional layer uses four-dimensional input and output in the format of (example, channel, height, width),
# where the batch size (number of examples in the batch) and the number of channels are both 1
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
lr = 3e-2 # Learning rate
for i in range(10):
Y_hat = conv2d(X)
l = (Y_hat - Y) ** 2
conv2d.zero_grad()
l.sum().backward()
# Update the kernel
conv2d.weight.data[:] -= lr * conv2d.weight.grad
if (i + 1) % 2 == 0:
print(f'epoch {i + 1}, loss {l.sum():.3f}')
# 输出
epoch 2, loss 16.481
epoch 4, loss 5.069
epoch 6, loss 1.794
epoch 8, loss 0.688
epoch 10, loss 0.274
学习的 kernel tensor:
# 与我们之前定义的核张量 K 非常接近
conv2d.weight.data.reshape((1, 2))
# 输出
tensor([[ 1.0398, -0.9328]])
7.2.5. Cross-Correlation and Convolution¶
交叉相关 (Cross-Correlation) 与卷积 (Convolution) 的关系:
核心差异:
交叉相关 (Cross-Correlation): 不翻转卷积核,直接在输入上滑动并计算加权和。
卷积 (Convolution): 在执行交叉相关之前,先将卷积核水平和垂直翻转,然后再进行滑动和计算。
交叉相关公式
卷积公式
- 核心区别:
交叉相关不对信号进行翻转,只是简单地滑动并计算重叠部分的内积。
卷积对信号进行翻转(即
𝑔(𝑡)→𝑔(−𝑡)),然后滑动并计算内积。
- 为什么深度学习中交叉相关和卷积无实质区别::
在深度学习中,卷积核 (filter) 是从数据中学习的。
不论卷积层执行的是严格卷积还是交叉相关,卷积核的学习过程都会自动调整,使得输出结果一致。
直观理解:卷积核在训练过程中是动态调整的,即便在数学上交叉相关和卷积稍有不同,训练后最终得到的卷积核已经隐含这种差异,使得两种操作的输出一致。
- 深度学习术语的约定俗成
尽管在严格意义上,交叉相关和卷积存在差异,但在深度学习文献中,交叉相关通常也直接被称为“卷积”。
这种约定使得术语更加简洁,避免在描述模型架构时反复强调二者的区别。
- 总结要点:
交叉相关与卷积: 数学上存在差异,卷积涉及卷积核的翻转,但在深度学习中通常不加以区分。
实质影响: 卷积核在训练过程中自动调整,因此不论执行交叉相关还是严格卷积,输出结果保持一致。
术语约定: 深度学习文献中,交叉相关操作通常直接称为卷积。
简化理解: 深度学习模型实现卷积层时,关注点在于卷积核的学习和特征提取效果,而非严格的数学定义差异。
7.2.6. Feature Map and Receptive Field¶
- 特征图 (Feature Map) 与感受野 (Receptive Field) 的定义
特征图 (Feature Map):特征图是卷积层的输出,它可以被看作是对输入空间维度(如宽度和高度)的学习表示。特征图在每一层提取输入数据的不同特征,供后续层进一步处理。
感受野 (Receptive Field):感受野是指卷积网络中某个元素 (如特征图中的一个像素) 受到前面哪些输入元素影响的范围。换句话说,感受野表示了输出中某个元素在输入中“看到”的区域大小。
- 关键点:
感受野不仅取决于当前层,还取决于所有前面层的累积影响。
感受野可以比输入本身更大,表示该位置的特征汇集了更大区域的信息。
- 直观理解:
每堆叠一层卷积,输出的感受野都会扩大,使得网络能够捕捉更广泛的空间信息。
- 总结要点:
特征图: 是卷积层输出的空间表示,用于提取输入的局部特征。
感受野: 指卷积层输出中某个元素在输入中“看到”的区域大小。感受野可以随着网络深度增加而扩大,帮助模型捕捉更大范围的信息。
层次特征提取: 较低层提取边缘和简单形状,高层提取复杂模式和语义特征。
生物启发: 卷积的设计灵感源于视觉皮层的研究,证明了卷积在生物和计算机视觉领域的有效性。
7.2.7. Summary¶
- 卷积层核心计算:
卷积层的核心计算是互相关 (cross-correlation) 操作。
计算互相关非常简单,使用一个嵌套的 for 循环即可完成,这表明卷积操作的计算是直接且局部的 (local)。
- 关键点:
局部性: 互相关只涉及输入数据的局部区域,这种局部操作在硬件优化方面非常重要。
矩阵运算: 当有多个输入和输出通道时,卷积层的计算相当于在通道之间进行矩阵乘法操作,进一步强调了计算的简洁性和局部性。
- 卷积的应用场景:
边缘检测 (Edge Detection): 识别图像中的边缘和轮廓。
线条检测 (Line Detection): 提取图像中的线条和形状。
图像模糊 (Blurring): 平滑图像,减少噪声。
图像锐化 (Sharpening): 增强图像的细节和对比度。
- 卷积核学习:
传统方法需要人工设计滤波器(如 Sobel 滤波器或 Canny 边缘检测),但卷积神经网络 (CNN) 能够直接从数据中学习最优的滤波器。
这种方式避免了复杂的特征工程,通过数据驱动的方法自动学习特征,极大提高了模型的表现能力。
核心优势:取代了手工设计特征的启发式方法,转而使用基于数据的统计方法来学习有效特征。
7.3. Padding and Stride¶
7.3.1. Padding¶
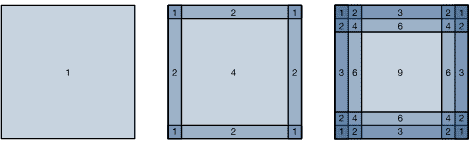
Fig. 7.3.1 Pixel utilization for convolutions of size 1x1, 2x2, and 3x3 respectively.¶
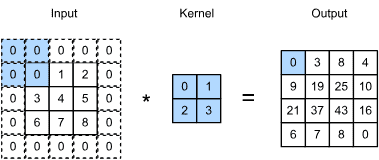
Fig. 7.3.2 Two-dimensional cross-correlation with padding.¶
In general, if we add a total of
In many cases, we will want to set
This will make it easier to predict the output shape of each layer when constructing the network.
所以,CNN 通常使用高度和宽度值为奇数的卷积核(
创建一个高度和宽度均为 3 的二维卷积层,并在所有侧面应用 1 个像素的填充。给定一个 height 和 width 为 8 的输入,我们发现输出的 height 和 width 也是 8
# We define a helper function to calculate convolutions.
# It initializes the convolutional layer weights and performs corresponding dimensionality elevations and reductions on the input and output
def comp_conv2d(conv2d, X):
# (1, 1) indicates that batch size and the number of channels are both 1
X = X.reshape((1, 1) + X.shape)
Y = conv2d(X)
# Strip the first two dimensions: examples and channels
return Y.reshape(Y.shape[2:])
# 1 row and column is padded on either side, so a total of 2 rows or columns are added
conv2d = nn.LazyConv2d(1, kernel_size=3, padding=1)
X = torch.rand(size=(8, 8))
comp_conv2d(conv2d, X).shape
当卷积核的高度和宽度不同时,我们可以通过为 height 和 width 设置不同的填充数来使 output 和 input 具有相同的 height 和 width:
# We use a convolution kernel with height 5 and width 3.
# The padding on either side of the height and width are 2 and 1, respectively
conv2d = nn.LazyConv2d(1, kernel_size=(5, 3), padding=(2, 1))
comp_conv2d(conv2d, X).shape
- 填充的作用和意义
核心作用:填充通过在输入图像的边缘添加额外像素(通常是零)来增加输出的高度和宽度。
- 目的:
防止输出尺寸缩小: 在卷积过程中,每次卷积都会导致输出尺寸缩小。如果不希望输出变小,可以使用填充保持输入和输出的尺寸一致。
保持所有像素的平等使用: 在无填充的情况下,边缘像素的使用频率较低。填充确保边缘像素与中心像素一样频繁地参与计算,从而提升模型对边缘特征的学习能力。
- 常见方式:
对称填充: 在输入图像的高度和宽度两侧均匀添加相同数量的像素,记作
简化记法: 如果垂直和水平填充相等,直接记作 p
- 零填充的优点
计算简单: 直接在图像边缘补零,计算和实现都很简单,硬件优化更容易。
隐含位置信息: CNN可以学习到填充值的分布,从而理解图像的边缘和中心区域的差异。
内存友好: 不需要额外分配大量内存,可以在卷积操作中隐式完成。
- 非零填充的情况
存在多种非零填充方法: 虽然零填充是最常用的,但也有其他方式(如镜像填充、重复边缘值等)。
使用场景: 通常只有在发现零填充带来不良的视觉或特征提取效果时,才会考虑使用其他类型的填充。
7.3.2. Stride¶
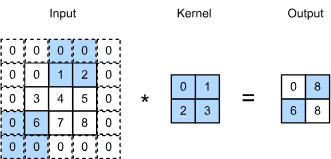
Fig. 7.3.3 Cross-correlation with strides of 3 and 2 for height and width, respectively.¶
改变步长的作用:
计算效率: 较大的步长可以减少计算量,因为滑动窗口覆盖的位置更少,输出张量的尺寸也更小。
下采样 (Downsampling): 较大的步长可以对输入进行下采样,减少分辨率的同时保留关键信息。
大卷积核: 如果卷积核较大,它本身已能捕获大范围的特征,此时使用较大步长可以减少冗余计算。
当 height 的 stride 为
If we set
进一步简化,输出尺寸 约 等于
将 height 和 width 的步幅都设置为 2,从而将输入的 height 和 width 减半:
X = torch.rand(size=(8, 8))
conv2d = nn.LazyConv2d(1, kernel_size=3, padding=1, stride=2)
comp_conv2d(conv2d, X).shape
# 输出
torch.Size([4, 4])
# shape计算过程
(n-k+s+1)/s = (8-3+2+1)/2 = 4
稍微复杂一点的例子:
conv2d = nn.LazyConv2d(1, kernel_size=(3, 5), padding=(0, 1), stride=(3, 4))
comp_conv2d(conv2d, X).shape
# 输出
torch.Size([2, 2])
# 说明
第一维: (8-3+0+3)/3 = 2.67 -> 2
第二维: (8-5+2+4)/4 = 2.25 -> 2
- 步幅的作用和意义
核心作用:步幅控制卷积窗口在输入图像上滑动的步长(移动距离)。
- 目的:
降低输出分辨率: 步幅大于1时,每次卷积窗口滑动会跳过部分位置,从而减少输出尺寸。例如,步幅为2时,输出的尺寸是输入的 1/2。
加速计算: 大步幅减少了卷积计算次数,提高了计算效率。
- 常见方式:
对称步幅: 如果水平和垂直步幅相同,直接记作 𝑠
默认设置: 填充默认为0,步幅默认为1,即不填充且滑动一个像素。
计算输出尺寸¶
GPT的输出(好像不对,待确定)
输入高度和宽度:H_in = 32, W_in = 32
卷积核大小:kernel_size = 3
步幅:stride = 1
填充:padding = 1
扩张率:dilation = 1
总结¶
- 填充和步幅是卷积层的重要超参数,它们影响输出尺寸、计算效率和特征提取效果。
填充: 保持尺寸一致,防止边缘信息丢失。
步幅: 控制分辨率,减少计算量。
7.4. Multiple Input and Multiple Output Channels¶
7.4.1. Multiple Input Channels¶
核心要点¶
- 多通道输入的卷积核心要求:
当输入数据有多个通道(channels)时,卷积核的通道数需要和输入数据的通道数相同,才能进行逐通道的交叉相关运算。
如果输入数据有
- 卷积核的结构:
当输入数据只有一个通道(
当输入数据有多个通道(
- 多通道卷积计算方式:
对每个通道分别进行二维交叉相关操作,然后将每个通道的结果相加,得到最终的输出。
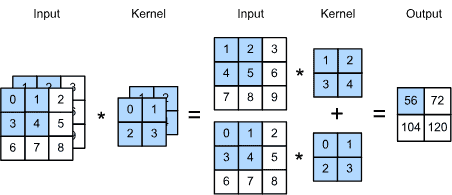
Fig. 7.4.1 Cross-correlation computation with two input channels.¶
实现具有多个 input 通道的交叉相关操作:
def corr2d_multi_in(X, K):
# Iterate through the 0th dimension (channel) of K first, then add them up
return sum(d2l.corr2d(x, k) for x, k in zip(X, K))
构造与图 7.4.1 中的值 K 相对应的输入张量 X 和核张量,以验证互相关运算的输出:
X = torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
[[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
K = torch.tensor([[[0.0, 1.0], [2.0, 3.0]],
[[1.0, 2.0], [3.0, 4.0]]])
corr2d_multi_in(X, K)
# 输出
tensor([[ 56., 72.],
[104., 120.]])
# 计算: n-k+1 = 3-2+1 = 2
# shape: torch.Size([2, 2])
7.4.2. Multiple Output Channels¶
要产生多个输出通道,需要为每个输出通道创建一个单独的卷积核。
此时,卷积核成为一个 4 维张量,形状为 (
其中 (
每个输出通道的结果都由其对应的卷积核计算得出,并从所有输入通道获取输入。
实现一个互相关函数来计算多个通道的输出:
def corr2d_multi_in_out(X, K):
# Iterate through the 0th dimension of K, and each time, perform cross-correlation operations with input X.
# All of the results are stacked together
return torch.stack([corr2d_multi_in(X, k) for k in K], 0)
We construct a trivial convolution kernel with three output channels by concatenating the kernel tensor for K with K+1 and K+2:
K = torch.stack((K, K + 1, K + 2), 0)
K.shape
# 输出
torch.Size([3, 2, 2, 2])
对 X 具有核张量的输入张量执行互相关运算 K:
corr2d_multi_in_out(X, K)
# 输出
tensor([[[ 56., 72.],
[104., 120.]],
[[ 76., 100.],
[148., 172.]],
[[ 96., 128.],
[192., 224.]]])
# shape计算过程
# shape: torch.Size([3, 2, 2])
7.4.3. 1x1 Convolutional Layer¶
1x1 卷积核不考虑高度和宽度维度上的相邻像素,仅在通道维度上进行操作。
它对输入图像中相同位置的元素进行线性组合。
可以将其视为在每个像素位置应用的全连接层,将 (
它需要 (
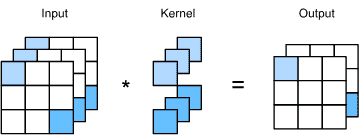
Fig. 7.4.2 The cross-correlation computation uses the convolution kernel with three input channels and two output channels. The input and output have the same height and width.¶
使用全连接层实现 1x1 卷积:
def corr2d_multi_in_out_1x1(X, K):
c_i, h, w = X.shape
c_o = K.shape[0]
X = X.reshape((c_i, h * w))
K = K.reshape((c_o, c_i))
# Matrix multiplication in the fully connected layer
Y = torch.matmul(K, X)
return Y.reshape((c_o, h, w))
用一些示例数据来检查:
X = torch.normal(0, 1, (3, 3, 3))
K = torch.normal(0, 1, (2, 3, 1, 1))
Y1 = corr2d_multi_in_out_1x1(X, K)
Y2 = corr2d_multi_in_out(X, K)
assert float(torch.abs(Y1 - Y2).sum()) < 1e-6
7.4.4. Discussion¶
- 计算成本
- 卷积操作复杂度:
- 给定一个大小为
ℎ×𝑤的图像,使用一个𝑘×𝑘的卷积核 计算复杂度是:
- 给定一个大小为
- 如果输入通道数是
复杂度增加为:
- 如果输入通道数是
- 计算示例:
对一个 256×256 的图像,使用 5×5 的卷积核,输入和输出通道数均为 128,计算量超过 530 亿次操作(乘法和加法分开计算)。
这是因为卷积操作不仅需要遍历整个图像,还要在所有通道上进行运算,计算量会迅速增加。
- 关键理解:
多通道增加了模型的表达能力,但也带来了计算成本的上升。
设计 CNN 结构时,需要在计算复杂度和模型表达能力之间找到平衡。
未来的模型设计中,降低计算成本是重要的研究方向之一。
7.5. Pooling¶
- 池化的目的:
减少卷积层对输入特征精确位置的敏感性,即提高平移不变性。这意味着即使特征稍微移动,模型仍然可以检测到它。
在空间上对特征表示进行下采样。这会降低特征图的空间分辨率,从而减少表示的大小,并加快计算速度
7.5.1. Maximum Pooling and Average Pooling¶
池化操作使用 固定形状的窗口(池化窗口) 在输入上滑动
与卷积层中 inputs 和 kernel 的互相关计算不同,池化层不包含任何参数(没有 kernel )
最大池化 (max-pooling) 计算每个池化窗口内的最大值
平均池化 (average pooling) 计算每个池化窗口内的平均值
在大多数情况下,最大池化优于平均池化。最大池化的概念源于认知神经科学,用于描述对象识别中信息的层级聚合
平均池化可以看作是对图像进行下采样的一种方式,通过组合多个相邻像素的信息来提高信噪比
- 池化如何工作:
池化窗口从左到右、从上到下滑动输入张量。
在每个位置,它计算窗口内输入子张量的最大值或平均值.
一个 (
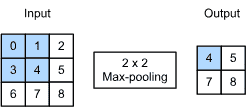
Fig. 7.5.1 Max-pooling with a pooling window shape of 2x2. The shaded portions are the first output element as well as the input tensor elements used for the output computation: max(0,1,3,4)=4 .说明:2x2滑动容器的最大池化就是,这获取4个元素里面的最大值¶
池化层的正向传播(不需要内核,将输出计算为输入中每个区域的最大值或平均值):
def pool2d(X, pool_size, mode='max'):
p_h, p_w = pool_size
Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
if mode == 'max':
Y[i, j] = X[i: i + p_h, j: j + p_w].max()
elif mode == 'avg':
Y[i, j] = X[i: i + p_h, j: j + p_w].mean()
return Y
验证二维最大池化层的输出:
X = torch.tensor([[0.0, 1.0, 2.0],
[3.0, 4.0, 5.0],
[6.0, 7.0, 8.0]])
pool2d(X, (2, 2))
# 输出
tensor([[4., 5.],
[7., 8.]])
平均池化层:
pool2d(X, (2, 2), 'avg')
# 输出
tensor([[2., 3.],
[5., 6.]])
7.5.2. Padding and Stride¶
用内置的二维 max-pooling 层来演示 padding 和 strides 在池化层中的使用:
X = torch.arange(16, dtype=torch.float32).reshape((1, 1, 4, 4))
X
# 输出
tensor([[[[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.]]]])
深度学习框架默认匹配池化窗口大小和步幅(if we use a pooling window of shape (3, 3) we get a stride shape of (3, 3) by default):
pool2d = nn.MaxPool2d(3)
# Pooling has no model parameters, hence it needs no initialization
pool2d(X)
# 输出
tensor([[[[10.]]]])
手动指定步幅和填充来覆盖框架默认值:
pool2d = nn.MaxPool2d(3, padding=1, stride=2)
pool2d(X)
# 输出
tensor([[[[ 5., 7.],
[13., 15.]]]])
指定一个任意高度和宽度的任意矩形池化窗口:
pool2d = nn.MaxPool2d((2, 3), stride=(2, 3), padding=(0, 1))
pool2d(X)
# 输出
tensor([[[[ 5., 7.],
[13., 15.]]]])
7.5.3. Multiple Channels¶
在处理多通道 input 数据时,pooling layer 单独池化每个 input 通道,而不是像卷积层那样在 channels 上对 inputs 求和。这意味着池化层的输出通道数与输入通道数相同
连接张 X 量 和 X + 1 通道维度,以构造具有两个通道的输入:
X = torch.cat((X, X + 1), 1) X # 输出 tensor([[[[ 0., 1., 2., 3.], [ 4., 5., 6., 7.], [ 8., 9., 10., 11.], [12., 13., 14., 15.]], [[ 1., 2., 3., 4.], [ 5., 6., 7., 8.], [ 9., 10., 11., 12.], [13., 14., 15., 16.]]]])
pooling 后 output channels 的数量仍然是 2:
pool2d = nn.MaxPool2d(3, padding=1, stride=2)
pool2d(X)
# tensor([[[[ 5., 7.],
[13., 15.]],
[[ 6., 8.],
[14., 16.]]]])
7.5.4. Summary¶
池化是一个非常简单的操作。
pooling 与 channels 无关,即,它保持 channels 数量不变,并且分别应用于每个 channel。
在两种流行的池化选项中,max-pooling 比 average pooling 更可取,因为它为 output 赋予了一定程度的不变性。
一种常见的选择是选择池化窗口大小 2x2 ,以将输出的原空间分辨率的四分之一。
- 扩展
stochastic pooling (Zeiler and Fergus, 2013)
fractional max-pooling (Graham, 2014)
7.6. Convolutional Neural Networks (LeNet)¶
7.6.1. LeNet¶
Fig. 7.6.1 Data flow in LeNet. The input is a handwritten digit, the output is a probability over 10 possible outcomes.¶
The basic units in each convolutional block are a convolutional layer, a sigmoid activation function, and a subsequent average pooling operation.
Each convolutional layer uses a 5x5 kernel and a sigmoid activation function.
这些层将空间排列的输入映射到许多二维特征图,通常会增加通道的数量。第一个卷积层有 6 个输出通道,而第二个卷积层有 16 个输出通道。
代码实现此类模型:
def init_cnn(module): #@save
"""Initialize weights for CNNs."""
if type(module) == nn.Linear or type(module) == nn.Conv2d:
nn.init.xavier_uniform_(module.weight)
class LeNet(d2l.Classifier): #@save
"""The LeNet-5 model."""
def __init__(self, lr=0.1, num_classes=10):
super().__init__()
self.save_hyperparameters()
self.net = nn.Sequential(
nn.LazyConv2d(6, kernel_size=5, padding=2), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.LazyConv2d(16, kernel_size=5), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Flatten(),
nn.LazyLinear(120), nn.Sigmoid(),
nn.LazyLinear(84), nn.Sigmoid(),
nn.LazyLinear(num_classes))
Fig. 7.6.2 Compressed notation for LeNet-5.¶
@d2l.add_to_class(d2l.Classifier) #@save
def layer_summary(self, X_shape):
X = torch.randn(*X_shape)
for layer in self.net:
X = layer(X)
print(layer.__class__.__name__, 'output shape:\t', X.shape)
model = LeNet()
model.layer_summary((1, 1, 28, 28))
# 输出
Conv2d output shape: torch.Size([1, 6, 28, 28])
Sigmoid output shape: torch.Size([1, 6, 28, 28])
AvgPool2d output shape: torch.Size([1, 6, 14, 14])
Conv2d output shape: torch.Size([1, 16, 10, 10])
Sigmoid output shape: torch.Size([1, 16, 10, 10])
AvgPool2d output shape: torch.Size([1, 16, 5, 5])
Flatten output shape: torch.Size([1, 400])
Linear output shape: torch.Size([1, 120])
Sigmoid output shape: torch.Size([1, 120])
Linear output shape: torch.Size([1, 84])
Sigmoid output shape: torch.Size([1, 84])
Linear output shape: torch.Size([1, 10])
7.6.2. Training¶
计算成本比类似深度的 MLP 更高:
trainer = d2l.Trainer(max_epochs=10, num_gpus=1)
data = d2l.FashionMNIST(batch_size=128)
model = LeNet(lr=0.1)
model.apply_init([next(iter(data.get_dataloader(True)))[0]], init_cnn)
trainer.fit(model, data)
8. Modern Convolutional Neural Networks¶
现代 CNN 不仅可以被使用 直接用于视觉任务,但它们也作为基本特征 用于更高级任务(例如跟踪)的生成器 ( Zhang et al. ,2021 ) ,分割 ( Long et al. ,2015 ) ,物体检测 ( Redmon 和 Farhadi,2018 ) ,或风格转变 (盖蒂斯等人,2016 ) 。
从 AlexNet 开始现代 CNN 之旅 ( Krizhevsky et al. ,2012 ) ,第一个大规模部署网络以击败传统计算机视觉方法 大规模的视力挑战;
VGG网络 ( Simonyan 和 Zisserman,2014 ) ,它利用了一些 重复的元素块;
网络中的网络 (NiN) 在输入上逐块卷积整个神经网络 (林等人,2013 ) ;
GoogLeNet 使用多分支卷积网络( Szegedy等人,2015 ) ;
残差网络(ResNet) ( He et al. ,2016 ) ,它仍然是计算机视觉中最流行的现成架构之一; ResNeXt 块( Xie et al. , 2017 )用于稀疏连接;
DenseNet ( Huang et al. ,2017 )用于残差架构的泛化。
8.1. Deep Convolutional Neural Networks (AlexNet)¶
8.1.1. Representation Learning¶
在 AlexNet 出现之前,卷积神经网络(CNN)在计算机视觉领域并未占据主导地位。尽管 LeNet 在早期的小型数据集上取得了不错的效果,但在更大的、更真实的数据集上训练 CNN 的性能和可行性尚未得到证实。
第一个现代 CNN(Krizhevsky 等人,2012)以其发明者之一 Alex Krizhevsky 的名字命名为 AlexNet,很大程度上是对 LeNet 的进化改进。它在2012年ImageNet挑战赛中取得了优异的表现。
AlexNet (2012) 及其前身 LeNet (1995) 共享许多架构元素。这就引出了一个问题:为什么花了这么长时间?一个关键的区别是,在过去的二十年里,可用的数据量和计算能力显着增加。因此,AlexNet 规模要大得多:与 1995 年可用的 CPU 相比,它使用更多的数据和更快的 GPU 进行训练。
8.1.2. AlexNet¶
AlexNet 采用 8 层 CNN,以大幅优势赢得了 2012 年 ImageNet 大规模视觉识别挑战赛 (Russakovsky et al., 2013)。该网络首次表明,通过学习获得的特征可以超越人工设计的特征,打破了计算机视觉以往的范式。
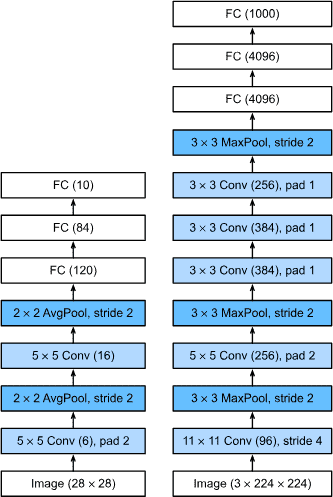
Fig. 8.1.2 From LeNet (left) to AlexNet (right).¶
class AlexNet(d2l.Classifier):
def __init__(self, lr=0.1, num_classes=10):
super().__init__()
self.save_hyperparameters()
self.net = nn.Sequential(
nn.LazyConv2d(96, kernel_size=11, stride=4, padding=1),
nn.ReLU(), nn.MaxPool2d(kernel_size=3, stride=2),
nn.LazyConv2d(256, kernel_size=5, padding=2), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.LazyConv2d(384, kernel_size=3, padding=1), nn.ReLU(),
nn.LazyConv2d(384, kernel_size=3, padding=1), nn.ReLU(),
nn.LazyConv2d(256, kernel_size=3, padding=1), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2), nn.Flatten(),
nn.LazyLinear(4096), nn.ReLU(), nn.Dropout(p=0.5),
nn.LazyLinear(4096), nn.ReLU(),nn.Dropout(p=0.5),
nn.LazyLinear(num_classes))
self.net.apply(d2l.init_cnn)
def layer_summary(self, X_shape):
X = d2l.randn(*X_shape)
for layer in self.net:
X = layer(X)
print(layer.__class__.__name__, 'output shape:\t', X.shape)
构造一个高和宽均为224的单通道数据示例来观察每一层的输出形状:
AlexNet().layer_summary((1, 1, 224, 224))
# 输出
Conv2d output shape: torch.Size([1, 96, 54, 54])
ReLU output shape: torch.Size([1, 96, 54, 54])
MaxPool2d output shape: torch.Size([1, 96, 26, 26])
Conv2d output shape: torch.Size([1, 256, 26, 26])
ReLU output shape: torch.Size([1, 256, 26, 26])
MaxPool2d output shape: torch.Size([1, 256, 12, 12])
Conv2d output shape: torch.Size([1, 384, 12, 12])
ReLU output shape: torch.Size([1, 384, 12, 12])
Conv2d output shape: torch.Size([1, 384, 12, 12])
ReLU output shape: torch.Size([1, 384, 12, 12])
Conv2d output shape: torch.Size([1, 256, 12, 12])
ReLU output shape: torch.Size([1, 256, 12, 12])
MaxPool2d output shape: torch.Size([1, 256, 5, 5])
Flatten output shape: torch.Size([1, 6400])
Linear output shape: torch.Size([1, 4096])
ReLU output shape: torch.Size([1, 4096])
Dropout output shape: torch.Size([1, 4096])
Linear output shape: torch.Size([1, 4096])
ReLU output shape: torch.Size([1, 4096])
Dropout output shape: torch.Size([1, 4096])
Linear output shape: torch.Size([1, 10])
8.1.3. Training¶
model = AlexNet(lr=0.01)
data = d2l.FashionMNIST(batch_size=128, resize=(224, 224)) # 使用 resize 参数执行此大小调整,为了适配模型改造的数据
trainer = d2l.Trainer(max_epochs=10, num_gpus=1)
trainer.fit(model, data)
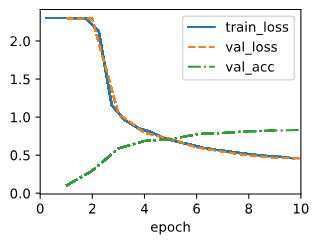
8.2. Networks Using Blocks (VGG)¶
VGG (Visual Geometry Group)
背景和概念演进¶
- 深度网络设计的演变
AlexNet 证明了深度卷积神经网络(CNN)的有效性,但没有提供通用的设计模板。
随着研究的发展,网络设计逐渐从单个神经元扩展到整层,再到如今的“模块化设计”,即基于重复模式的块(blocks)。这种模块化理念源自芯片设计领域中逻辑单元到逻辑块的抽象过程。
- VGG 的提出
VGG 是由牛津大学的视觉几何组(Visual Geometry Group)提出的网络,其核心创新是通过重复的卷积块设计深度网络。
VGG 的设计旨在探索深层网络与宽网络的性能差异,最终验证了深而窄的网络在性能上优于浅而宽的网络。
VGG 的核心设计¶
8.2.1. VGG Blocks¶
一个 VGG 块由多个 3x3 的卷积层组成,每个卷积层后接一个非线性激活(如 ReLU),再接一个 2x2 的最大池化层(stride 为 2)。
使用多个 3x3 卷积层替代单个较大卷积(如 5x5 或 7x7),既能减少参数数量,又能提高性能。
def vgg_block(num_convs, out_channels):
layers = []
for _ in range(num_convs):
layers.append(nn.LazyConv2d(out_channels, kernel_size=3, padding=1))
layers.append(nn.ReLU())
layers.append(nn.MaxPool2d(kernel_size=2,stride=2))
return nn.Sequential(*layers)
8.2.2. VGG Network¶
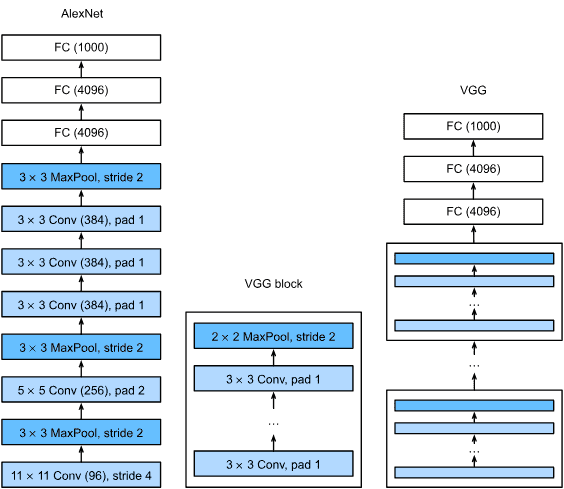
Fig. 8.2.1 From AlexNet to VGG. The key difference is that VGG consists of blocks of layers, whereas AlexNet’s layers are all designed individually.¶
- VGG 网络可以划分为两部分:
卷积部分:由多个 VGG 块组成,逐渐减少空间分辨率。
全连接部分:与 AlexNet 类似,包含多个全连接层。
原始 VGG-11 网络包括 5 个卷积块,最初的两个块各有 1 层卷积,后三个块各有 2 层卷积。每个块的输出通道数逐步翻倍,从 64 增加到 512。
class VGG(d2l.Classifier):
def __init__(self, arch, lr=0.1, num_classes=10):
super().__init__()
self.save_hyperparameters()
conv_blks = []
for (num_convs, out_channels) in arch:
conv_blks.append(vgg_block(num_convs, out_channels))
self.net = nn.Sequential(
*conv_blks,
nn.Flatten(),
nn.LazyLinear(4096), nn.ReLU(), nn.Dropout(0.5),
nn.LazyLinear(4096), nn.ReLU(), nn.Dropout(0.5),
nn.LazyLinear(num_classes))
self.net.apply(d2l.init_cnn)
8.2.3. Training¶
model = VGG(arch=((1, 16), (1, 32), (2, 64), (2, 128), (2, 128)), lr=0.01)
trainer = d2l.Trainer(max_epochs=10, num_gpus=1)
data = d2l.FashionMNIST(batch_size=128, resize=(224, 224))
model.apply_init([next(iter(data.get_dataloader(True)))[0]], d2l.init_cnn)
trainer.fit(model, data)
意义和扩展¶
- VGG 的贡献
VGG 是首个真正现代化的 CNN 网络,引入了“模块化设计”的理念,通过深而窄的架构显著提升性能。
它开创了设计“网络家族”的趋势,即通过调整块的数量和参数,形成具有不同性能和复杂度的网络变体。
- 性能权衡
在实际应用中,设计者可以根据需要在速度和精度之间找到适合的平衡点。
- 新方向
最近的研究(如 ParNet)表明,通过更多并行计算,浅层网络也可以实现竞争性性能,这可能为未来的网络架构设计提供新思路。
总结¶
VGG 的设计不仅奠定了现代深度学习网络的基础,也为深度学习的普及和快速实现提供了便利。其模块化设计思想至今仍被后续研究广泛借鉴。
8.3. Network in Network (NiN)¶
NiN 网络在 LeNet、AlexNet 和 VGG 的基础上进一步改进
VGG 等这些网络通过卷积层和池化层提取空间特征,并通过全连接层进行后续处理。
- 这种设计存在两个主要问题:
全连接层参数量大:传统的全连接层需要大量的参数和内存,例如 VGG-11 的全连接层就占据了近 400MB 内存。这在移动设备和嵌入式设备上难以实现。
无法在网络早期引入全连接层:在网络早期引入全连接层会破坏空间结构,同时还会进一步增加内存需求。
- NiN 的创新点
1x1 卷积:作为局部全连接层,在不改变空间维度的情况下为每个像素位置添加非线性。
全局平均池化:在网络最后一层通过全局平均池化整合空间信息,完全替代全连接层,大幅减少参数量。
8.3.1. NiN Blocks¶
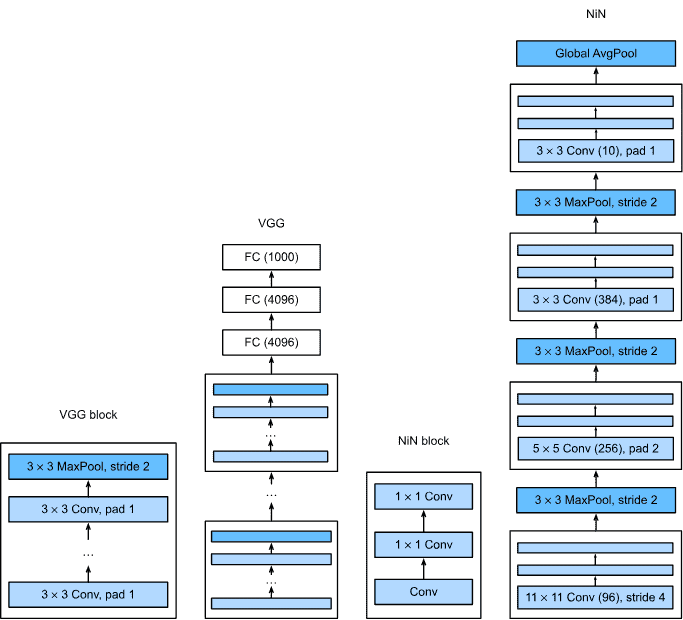
Fig. 8.3.1 Comparing the architectures of VGG and NiN, and of their blocks.¶
注意 NiN 块中的差异(初始卷积后面是 1x1 卷积,而 VGG 保留 3x3 卷积)以及最后我们不再需要巨大的全连接层。
- 结构特点
卷积设计:初始卷积层与 AlexNet 类似,使用 11x11、5x5 和 3x3 的卷积核。
NiN 块:每个块包含一个标准卷积层,后接两个 1x1 卷积层,提升特征提取效率。
全局平均池化:在最后的特征表示层通过全局平均池化代替全连接层,用于生成分类的 logits。
- 优势
参数量显著减少:不需要大型的全连接层,适合内存受限的设备。
提升平移不变性:全局平均池化增强了模型对平移的鲁棒性。
提高非线性建模能力:通过 1x1 卷积在每个位置捕获通道间的交互,提高网络表达能力。
def nin_block(out_channels, kernel_size, strides, padding):
return nn.Sequential(
nn.LazyConv2d(out_channels, kernel_size, strides, padding), nn.ReLU(),
nn.LazyConv2d(out_channels, kernel_size=1), nn.ReLU(),
nn.LazyConv2d(out_channels, kernel_size=1), nn.ReLU())
8.3.2. NiN Model¶
NiN 与 AlexNet 和 VGG 之间的第二个显着区别是 NiN 完全避免了全连接层。
NiN 使用 NiN 块,其输出通道数等于标签类的数量,后跟全局平均池化层,产生 logits 向量。这种设计显着减少了所需模型参数的数量,但代价是可能会增加训练时间。
class NiN(d2l.Classifier):
def __init__(self, lr=0.1, num_classes=10):
super().__init__()
self.save_hyperparameters()
self.net = nn.Sequential(
nin_block(96, kernel_size=11, strides=4, padding=0),
nn.MaxPool2d(3, stride=2),
nin_block(256, kernel_size=5, strides=1, padding=2),
nn.MaxPool2d(3, stride=2),
nin_block(384, kernel_size=3, strides=1, padding=1),
nn.MaxPool2d(3, stride=2),
nn.Dropout(0.5),
nin_block(num_classes, kernel_size=3, strides=1, padding=1),
nn.AdaptiveAvgPool2d((1, 1)),
nn.Flatten())
self.net.apply(d2l.init_cnn)
创建一个数据示例来查看每个块的输出形状:
NiN().layer_summary((1, 1, 224, 224))
# 输出
Sequential output shape: torch.Size([1, 96, 54, 54])
MaxPool2d output shape: torch.Size([1, 96, 26, 26])
Sequential output shape: torch.Size([1, 256, 26, 26])
MaxPool2d output shape: torch.Size([1, 256, 12, 12])
Sequential output shape: torch.Size([1, 384, 12, 12])
MaxPool2d output shape: torch.Size([1, 384, 5, 5])
Dropout output shape: torch.Size([1, 384, 5, 5])
Sequential output shape: torch.Size([1, 10, 5, 5])
AdaptiveAvgPool2d output shape: torch.Size([1, 10, 1, 1])
Flatten output shape: torch.Size([1, 10])
8.3.3. Training¶
model = NiN(lr=0.05)
trainer = d2l.Trainer(max_epochs=10, num_gpus=1)
data = d2l.FashionMNIST(batch_size=128, resize=(224, 224))
model.apply_init([next(iter(data.get_dataloader(True)))[0]], d2l.init_cnn)
trainer.fit(model, data)
8.3.4. Summary¶
NiN 的参数比 AlexNet 和 VGG 少得多。这主要源于这样一个事实:它不需要巨大的全连接层。相反,它使用全局平均池来聚合网络主体最后阶段之后的所有图像位置。这消除了对昂贵的(学习的)归约操作的需要,并用简单的平均值代替它们。
选择较少的宽核卷积并将其替换为 1x1 卷积有助于进一步减少参数。它可以满足任何给定位置内跨通道的大量非线性。 1x1 卷积和全局平均池化都显着影响了后续的 CNN 设计。
【影响】NiN 的 1x1 卷积和全局平均池化设计对后续的 CNN 网络架构产生了深远影响,使得模型在保持高准确率的同时变得更加高效。
8.4. Multi-Branch Networks (GoogLeNet)¶
2014 年,GoogLeNet 赢得了 ImageNet 挑战赛(Szegedy 等人,2015 年),其结构结合了 NiN(Lin 等人,2013 年)、重复块(Simonyan 和 Zisserman,2014 年)以及混合卷积的优点内核。
GoogLeNet 的关键贡献是网络主体的设计。它巧妙地解决了卷积核选择的问题。
设计概述¶
- 创新点
NiN(Network in Network) 的思想,即利用 1x1 卷积来提取特征并减少计算量。
重复模块的设计,类似于VGG网络的模块化思想。
多种卷积核的结合,通过多分支结构同时使用不同大小的卷积核,而不是单独选择某一种。
- GoogLeNet首次明确了卷积神经网络的三部分结构:
- Stem(输入部分):
前两三个卷积层,用于提取低级特征。
以AlexNet和LeNet为基础的 7x7 卷积和最大池化。
- Body(主体部分):
多个卷积块,用于深层次特征提取。
每组包含多个Inception块,依次增加通道数。
- Head(输出部分):
将提取的特征映射到特定的任务(分类、检测等)。
通过全局平均池化,直接输出分类结果。
8.4.1. Inception Blocks¶
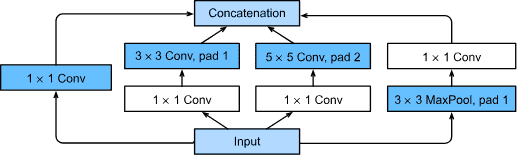
Fig. 8.4.1 Structure of the Inception block.(GoogLeNet 中的基本卷积块称为 Inception 块)¶
- 起始块由四个并行分支组成。
使用 1x1 卷积提取低级特征。
使用 1x1 卷积降维后,再用 3x3 卷积提取中等尺度特征。
使用 1x1 卷积降维后,再用 5x5 卷积提取更大尺度特征。
使用 3x3 最大池化后,再用 1x1 卷积改变通道数。
最后,每个分支的输出沿着通道维度连接并构成块的输出。
关键超参数:每层的输出通道数,决定了不同分支分配的容量大小。
class Inception(nn.Module):
# c1--c4 are the number of output channels for each branch
def __init__(self, c1, c2, c3, c4, **kwargs):
super(Inception, self).__init__(**kwargs)
# Branch 1
self.b1_1 = nn.LazyConv2d(c1, kernel_size=1)
# Branch 2
self.b2_1 = nn.LazyConv2d(c2[0], kernel_size=1)
self.b2_2 = nn.LazyConv2d(c2[1], kernel_size=3, padding=1)
# Branch 3
self.b3_1 = nn.LazyConv2d(c3[0], kernel_size=1)
self.b3_2 = nn.LazyConv2d(c3[1], kernel_size=5, padding=2)
# Branch 4
self.b4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
self.b4_2 = nn.LazyConv2d(c4, kernel_size=1)
def forward(self, x):
b1 = F.relu(self.b1_1(x))
b2 = F.relu(self.b2_2(F.relu(self.b2_1(x))))
b3 = F.relu(self.b3_2(F.relu(self.b3_1(x))))
b4 = F.relu(self.b4_2(self.b4_1(x)))
return torch.cat((b1, b2, b3, b4), dim=1)
8.4.2. GoogLeNet Model¶
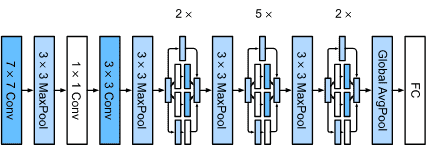
Fig. 8.4.2 The GoogLeNet architecture.¶
GoogLeNet 使用总共 9 个初始块的堆栈,分为三组,中间有最大池化,头部有全局平均池化来生成估计。
初始块之间的最大池化降低了维度。
第一个模块使用 64 通道 7x7 卷积层:
class GoogleNet(d2l.Classifier):
def b1(self):
return nn.Sequential(
nn.LazyConv2d(64, kernel_size=7, stride=2, padding=3),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
第二个模块使用两个卷积层:首先是 64 通道 1x1 卷积层,然后是通道数量增加三倍的 3x3 卷积层:
@d2l.add_to_class(GoogleNet)
def b2(self):
return nn.Sequential(
nn.LazyConv2d(64, kernel_size=1), nn.ReLU(),
nn.LazyConv2d(192, kernel_size=3, padding=1), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
第三个模块串联两个完整的Inception块:
# 第一个 Inception 块的输出通道数为: 64+128+32+32 = 256
# 第二个 Inception 块的输出通道数为: 128+192+96+64 = 480
@d2l.add_to_class(GoogleNet)
def b3(self):
return nn.Sequential(Inception(64, (96, 128), (16, 32), 32),
Inception(128, (128, 192), (32, 96), 64),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
第四个模块比较复杂。它串联连接了五个 Inception 块:
@d2l.add_to_class(GoogleNet)
def b4(self):
return nn.Sequential(Inception(192, (96, 208), (16, 48), 64),
Inception(160, (112, 224), (24, 64), 64),
Inception(128, (128, 256), (24, 64), 64),
Inception(112, (144, 288), (32, 64), 64),
Inception(256, (160, 320), (32, 128), 128),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
第五个模块带有两个 Inception 块:
@d2l.add_to_class(GoogleNet)
def b5(self):
return nn.Sequential(Inception(256, (160, 320), (32, 128), 128),
Inception(384, (192, 384), (48, 128), 128),
nn.AdaptiveAvgPool2d((1,1)), nn.Flatten())
将它们全部组装成一个完整的网络:
@d2l.add_to_class(GoogleNet)
def __init__(self, lr=0.1, num_classes=10):
super(GoogleNet, self).__init__()
self.save_hyperparameters()
self.net = nn.Sequential(self.b1(), self.b2(), self.b3(), self.b4(),
self.b5(), nn.LazyLinear(num_classes))
self.net.apply(d2l.init_cnn)
看看各个模块之间输出形状的变化:
model = GoogleNet().layer_summary((1, 1, 96, 96))
# 输出
Sequential output shape: torch.Size([1, 64, 24, 24])
Sequential output shape: torch.Size([1, 192, 12, 12])
Sequential output shape: torch.Size([1, 480, 6, 6])
Sequential output shape: torch.Size([1, 832, 3, 3])
Sequential output shape: torch.Size([1, 1024])
Linear output shape: torch.Size([1, 10])
8.4.3. Training¶
model = GoogleNet(lr=0.01)
trainer = d2l.Trainer(max_epochs=10, num_gpus=1)
data = d2l.FashionMNIST(batch_size=128, resize=(96, 96))
model.apply_init([next(iter(data.get_dataloader(True)))[0]], d2l.init_cnn)
trainer.fit(model, data)
8.4.4. Discussion¶
GoogLeNet 的一个关键特征是,它的计算成本实际上比其前身更便宜,同时提供更高的准确性。
现在,您可以自豪地实现了可以说是第一个真正现代的 CNN。
- 优势
多尺度特征提取:通过并行使用不同大小的卷积核,能够有效捕获图像的细节和全局信息。
参数高效:利用 1x1 卷积降维和全局平均池化,显著减少了参数量。
模块化设计:方便扩展和调整,适合深度学习模型的快速迭代。
8.5. Batch Normalization¶
训练深度神经网络很难,特别是在收敛速度和稳定性上。
批量归一化通过标准化中间层的激活值,解决了激活分布漂移的问题,从而加速训练并提高模型稳定性。
它还有额外的正则化效果,可以减少过拟合。
8.5.1. Training Deep Networks¶
批量归一化通过在每个训练步骤中对输入进行标准化,得到零均值和单位方差:
- 批量归一化具有以下优点:
预处理:标准化激活值,减少梯度爆炸或消失问题。
数值稳定性:使优化器能使用更大的学习率。
正则化:引入了噪声,有效减少过拟合。
8.5.2. Batch Normalization Layers¶
8.5.2.1. Fully Connected Layers¶
通常应用在仿射变换之后,激活函数之前:
8.5.2.2. Convolutional Layers¶
对于卷积层,我们可以在卷积之后但非线性激活函数之前应用批量归一化。与全连接层中的批量归一化的主要区别在于,我们在所有位置的每个通道的基础上应用该操作。
- 对每个通道独立标准化:
汇总所有空间位置的值(例如卷积输出的高度和宽度)来计算均值和方差。
每个通道有自己的缩放和偏移参数。
8.5.2.3. Layer Normalization¶
针对小批量(甚至批量大小为1)或序列任务,层归一化对每个样本的所有特征进行标准化:
独立于批量大小,适用于单样本场景。
避免了因小批量引入的不稳定性。
8.5.2.4. Batch Normalization During Prediction¶
8.5.3. Implementation from Scratch¶
def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
# Use is_grad_enabled to determine whether we are in training mode
if not torch.is_grad_enabled():
# In prediction mode, use mean and variance obtained by moving average
X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
else:
assert len(X.shape) in (2, 4)
if len(X.shape) == 2:
# When using a fully connected layer, calculate the mean and
# variance on the feature dimension
mean = X.mean(dim=0)
var = ((X - mean) ** 2).mean(dim=0)
else:
# When using a two-dimensional convolutional layer, calculate the
# mean and variance on the channel dimension (axis=1). Here we
# need to maintain the shape of X, so that the broadcasting
# operation can be carried out later
mean = X.mean(dim=(0, 2, 3), keepdim=True)
var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)
# In training mode, the current mean and variance are used
X_hat = (X - mean) / torch.sqrt(var + eps)
# Update the mean and variance using moving average
moving_mean = (1.0 - momentum) * moving_mean + momentum * mean
moving_var = (1.0 - momentum) * moving_var + momentum * var
Y = gamma * X_hat + beta # Scale and shift
return Y, moving_mean.data, moving_var.data
class BatchNorm(nn.Module):
# num_features: the number of outputs for a fully connected layer
# or the number of output channels for a convolutional layer.
# num_dims: 2 for a fully connected layer and 4 for a convolutional layer
def __init__(self, num_features, num_dims):
super().__init__()
if num_dims == 2:
shape = (1, num_features)
else:
shape = (1, num_features, 1, 1)
# The scale parameter and the shift parameter (model parameters) are initialized to 1 and 0
self.gamma = nn.Parameter(torch.ones(shape))
self.beta = nn.Parameter(torch.zeros(shape))
# The variables that are not model parameters are initialized to 0 and 1
self.moving_mean = torch.zeros(shape)
self.moving_var = torch.ones(shape)
def forward(self, X):
# If X is not on the main memory, copy moving_mean and moving_var to the device where X is located
if self.moving_mean.device != X.device:
self.moving_mean = self.moving_mean.to(X.device)
self.moving_var = self.moving_var.to(X.device)
# Save the updated moving_mean and moving_var
Y, self.moving_mean, self.moving_var = batch_norm(
X, self.gamma, self.beta, self.moving_mean,
self.moving_var, eps=1e-5, momentum=0.1)
return Y
8.5.4. LeNet with Batch Normalization¶
class BNLeNetScratch(d2l.Classifier):
def __init__(self, lr=0.1, num_classes=10):
super().__init__()
self.save_hyperparameters()
self.net = nn.Sequential(
nn.LazyConv2d(6, kernel_size=5), BatchNorm(6, num_dims=4),
nn.Sigmoid(), nn.AvgPool2d(kernel_size=2, stride=2),
nn.LazyConv2d(16, kernel_size=5), BatchNorm(16, num_dims=4),
nn.Sigmoid(), nn.AvgPool2d(kernel_size=2, stride=2),
nn.Flatten(), nn.LazyLinear(120),
BatchNorm(120, num_dims=2), nn.Sigmoid(), nn.LazyLinear(84),
BatchNorm(84, num_dims=2), nn.Sigmoid(),
nn.LazyLinear(num_classes))
trainer = d2l.Trainer(max_epochs=10, num_gpus=1)
data = d2l.FashionMNIST(batch_size=128)
model = BNLeNetScratch(lr=0.1)
model.apply_init([next(iter(data.get_dataloader(True)))[0]], d2l.init_cnn)
trainer.fit(model, data)
model.net[1].gamma.reshape((-1,)), model.net[1].beta.reshape((-1,))
8.5.5. Concise Implementation¶
class BNLeNet(d2l.Classifier):
def __init__(self, lr=0.1, num_classes=10):
super().__init__()
self.save_hyperparameters()
self.net = nn.Sequential(
nn.LazyConv2d(6, kernel_size=5), nn.LazyBatchNorm2d(),
nn.Sigmoid(), nn.AvgPool2d(kernel_size=2, stride=2),
nn.LazyConv2d(16, kernel_size=5), nn.LazyBatchNorm2d(),
nn.Sigmoid(), nn.AvgPool2d(kernel_size=2, stride=2),
nn.Flatten(), nn.LazyLinear(120), nn.LazyBatchNorm1d(),
nn.Sigmoid(), nn.LazyLinear(84), nn.LazyBatchNorm1d(),
nn.Sigmoid(), nn.LazyLinear(num_classes))
trainer = d2l.Trainer(max_epochs=10, num_gpus=1)
data = d2l.FashionMNIST(batch_size=128)
model = BNLeNet(lr=0.1)
model.apply_init([next(iter(data.get_dataloader(True)))[0]], d2l.init_cnn)
trainer.fit(model, data)
8.6. Residual Networks (ResNet) and ResNeXt¶
残差网络 (ResNet)
何凯明等人2016年提出的残差网络(ResNet),该网络引入了残差块(residual block),其核心思想是让每一层除了学习到期望的底层映射外,还能更轻松地包含恒等映射作为一个元素。这解决了非常深的网络难以训练的问题,并且ResNet在2015年的ImageNet大规模视觉识别挑战赛中取得了胜利。此设计对后续深度神经网络的发展有着深远的影响。
残差块的工作原理:输入可以直接跳过某些层传递到后面的层,形成所谓的“残差连接”或“捷径连接”。这样做的好处是可以使网络更容易学习到恒等映射,因为当需要学习的映射为恒等映射时,网络只需将权重调整为零即可。
8.7. Densely Connected Networks (DenseNet)¶
主要讲了DenseNet(密集连接网络)相较于 ResNet 的特点、数学原理以及实现方式。
核心概念¶
密集连接模式:DenseNet 的每一层与之前所有层相连接。这种连接方式通过 特征级拼接(concatenation) 来保留和复用特征,而不是像 ResNet 中通过相加(addition)连接。
特征复用:每一层的输出作为后续层的输入,这样可以确保每层都能直接访问最初输入和每层中间结果,从而减少信息丢失。
关键组成部分¶
- Dense Block(密集块):
每个 Dense Block 包括多个卷积块,输入和每个卷积块的输出在通道维度上拼接。
生长率:每个 Dense Block 增加输出通道数的速率。
- Transition Layer(过渡层):
控制模型复杂度,减少通道数并通过平均池化降低分辨率。
使用
DenseNet 的优点¶
高效特征复用:每层的特征都直接提供给后续层,减少冗余计算。
更轻的模型:相比 ResNet,DenseNet 在参数量上更高效。
缓解梯度消失问题:密集连接模式提供了更短的梯度传播路径。
8.8. Designing Convolution Network Architectures¶
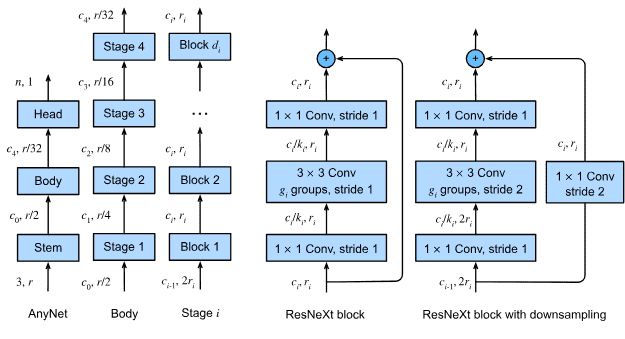
Fig. 8.8.1 The AnyNet design space.¶
The numbers
cand the resolution- From left to right: generic network structure composed of
stem,body, andhead; body composed of four stages;
detailed structure of a stage;
- two alternative structures for blocks,
one without downsampling and one that halves the resolution in each dimension.
- Design choices include
depth
the number of output channels
the number of groups
and bottleneck ratio
- From left to right: generic network structure composed of
传统架构设计的直觉性¶
早期的 CNN 架构(如 AlexNet 和 VGG)依赖科学家的直觉设计。
常见方法包括堆叠卷积层(如 3x3 卷积)来增加深度,以提升网络性能。
NiN 引入了 1x1 卷积,解决了局部非线性问题,并优化了信息聚合。
GoogLeNet 的多分支设计(Inception 模块)结合了 VGG 和 NiN 的优点。
ResNet 改变了归纳偏置,通过引入残差连接使得训练更深的网络成为可能。
SENet 和 ResNeXt 等后续架构进一步优化了网络计算效率和参数权衡。
神经架构搜索(NAS)¶
NAS 是通过自动化方法(如遗传算法、强化学习)探索最佳网络架构。
虽然 NAS 能生成高性能网络(如 EfficientNets),但其计算成本极高。
RegNet 与设计空间优化¶
相比寻找“单一最佳网络”,探索整个网络设计空间更有价值。
Radosavovic 等人提出了一种结合手动设计和 NAS 优势的方法,通过优化网络分布,而非单一实例,得到了 RegNet 系列。
RegNet 提供了性能良好的 CNN 设计指导原则,强调在设计过程中既要科学探索,又要保证计算成本低廉。
AnyNet 设计空间¶
AnyNet 是一个通用的设计模板,由“stem”(初始处理)、“body”(核心计算)和“head”(输出层)组成。
设计的核心在于“body”,它通过多个阶段和模块(如 ResNeXt 块)逐步提取特征。
为了有效探索设计空间,需要调整诸多参数(如通道数、深度、分组数等)并优化它们的组合。
分布优化与假设¶
网络性能优化的目标从寻找单一最佳参数,转为寻找“好的参数分布”。
- 假设包括:
好的设计原则存在,并适用于多个网络。
不需要完全训练网络,早期性能可以提供指导。
小规模实验结果可以推广到大规模网络。
设计问题可以分解成相对独立的模块。
9. Recurrent Neural Networks¶
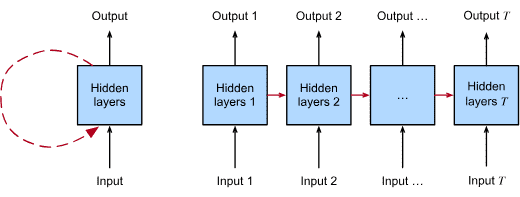
Fig. 9.1 On the left recurrent connections are depicted via cyclic edges. On the right, we unfold the RNN over time steps. Here, recurrent edges span adjacent time steps, while conventional connections are computed synchronously.¶
RNN 在 2010 年代开始流行(Graves 等人,2008 年) )、机器翻译(Sutskever 等人,2014)以及识别医疗诊断(Lipton 等人,2016)。
9.1. Working with Sequences¶
1. 序列数据的特点¶
传统单输入模型:之前我们讨论的模型输入是单一特征向量
序列输入的区别:序列输入由一组按时间顺序排列的特征向量
序列数据的例子包括:
文档序列:每个文档是一组单词序列。
医院患者数据:一个住院过程由一系列事件组成。
股票价格序列:按时间记录的股价数据。
在序列数据中,相邻时间步的数据通常存在依赖关系(如单词之间的上下文关系或患者治疗方案的时间顺序),而不是独立采样的。
2. 序列建模的目标¶
预测固定目标:如根据影评文本判断情感(正向或负向)。
预测序列目标:如根据图片生成描述文本。
序列到序列建模:如机器翻译,将一个语言的句子转换为另一语言。
3. 序列建模的基本方法¶
9.1.1. Autoregressive Models¶
目标:通过历史数据
问题:历史数据的长度随着时间增长,输入特征的数量也随之越来越长。
- 解决方法:
限制窗口大小:仅考虑固定长度窗口
隐变量表示:用一个隐藏状态
9.1.2. Sequence Models(Markov Models)¶
如果可以仅依赖最近的
一阶马尔科夫模型:只考虑最近的一个时间步
虽然实际数据可能不完全符合马尔科夫条件,但在实际应用中,这种近似简化了计算。
4. 语言模型与序列模型¶
语言模型 (Language Model)¶
用于估计整个序列(如句子)的联合概率
利用链式法则,将联合概率分解为条件概率的乘积:
语言模型可用于自然语言生成、语音识别、机器翻译等任务。
解码顺序¶
一般从左到右建模(与阅读习惯一致),因为预测相邻单词更容易。
未来事件可能影响后续结果,但不会影响过去。
5. 实际应用¶
股票价格预测:如通过历史股价数据预测下一时刻价格。
患者病程建模:根据前几天的治疗方案,预测第十天的用药。
文本生成与补全:基于已知前缀,预测可能的后续文本。
9.2. Converting Raw Text into Sequence Data¶
Typical preprocessing pipelines execute the following steps:
1. Load text as strings into memory.
2. Split the strings into tokens (e.g., words or characters).
3. Build a vocabulary dictionary to associate each vocabulary element with a numerical index.
4. Convert the text into sequences of numerical indices.
9.2.1. Reading the Dataset¶
class TimeMachine(d2l.DataModule): #@save
"""The Time Machine dataset."""
def _download(self):
fname = d2l.download(d2l.DATA_URL + 'timemachine.txt', self.root,
'090b5e7e70c295757f55df93cb0a180b9691891a')
with open(fname) as f:
return f.read()
data = TimeMachine()
raw_text = data._download()
raw_text[:60]
@d2l.add_to_class(TimeMachine) #@save
def _preprocess(self, text):
return re.sub('[^A-Za-z]+', ' ', text).lower()
text = data._preprocess(raw_text)
text[:60]
# 输出
# 'the time machine by h g wells i the time traveller for so it'
9.2.2. Tokenization¶
@d2l.add_to_class(TimeMachine) #@save
def _tokenize(self, text):
return list(text)
tokens = data._tokenize(text)
','.join(tokens[:30])
# 输出
# 't,h,e, ,t,i,m,e, ,m,a,c,h,i,n,e, ,b,y, ,h, ,g, ,w,e,l,l,s, '
9.2.3. Vocabulary¶
class Vocab: #@save
"""Vocabulary for text."""
def __init__(self, tokens=[], min_freq=0, reserved_tokens=[]):
# Flatten a 2D list if needed
if tokens and isinstance(tokens[0], list):
tokens = [token for line in tokens for token in line]
# Count token frequencies
counter = collections.Counter(tokens)
self.token_freqs = sorted(counter.items(), key=lambda x: x[1],
reverse=True)
# The list of unique tokens
self.idx_to_token = list(sorted(set(['<unk>'] + reserved_tokens + [
token for token, freq in self.token_freqs if freq >= min_freq])))
self.token_to_idx = {token: idx
for idx, token in enumerate(self.idx_to_token)}
def __len__(self):
return len(self.idx_to_token)
def __getitem__(self, tokens):
if not isinstance(tokens, (list, tuple)):
return self.token_to_idx.get(tokens, self.unk)
return [self.__getitem__(token) for token in tokens]
def to_tokens(self, indices):
if hasattr(indices, '__len__') and len(indices) > 1:
return [self.idx_to_token[int(index)] for index in indices]
return self.idx_to_token[indices]
@property
def unk(self): # Index for the unknown token
return self.token_to_idx['<unk>']
使用:
vocab = Vocab(tokens)
indices = vocab[tokens[:10]]
print('indices:', indices)
print('words:', vocab.to_tokens(indices))
# 输出
# indices: [21, 9, 6, 0, 21, 10, 14, 6, 0, 14]
# words: ['t', 'h', 'e', ' ', 't', 'i', 'm', 'e', ' ', 'm']
9.2.4. Putting It All Together¶
@d2l.add_to_class(TimeMachine) #@save
def build(self, raw_text, vocab=None):
tokens = self._tokenize(self._preprocess(raw_text))
if vocab is None: vocab = Vocab(tokens)
corpus = [vocab[token] for token in tokens]
return corpus, vocab
corpus, vocab = data.build(raw_text)
len(corpus), len(vocab)
# (173428, 28)
9.2.5. Exploratory Language Statistics¶
使用真实的语料库和针对单词定义的 Vocab 类:
words = text.split()
vocab = Vocab(words)
vocab.token_freqs[:10]
# 输出
[('the', 2261),
('i', 1267),
('and', 1245),
('of', 1155),
('a', 816),
('to', 695),
('was', 552),
('in', 541),
('that', 443),
('my', 440)]
bigram_tokens = ['--'.join(pair) for pair in zip(words[:-1], words[1:])]
bigram_vocab = Vocab(bigram_tokens)
bigram_vocab.token_freqs[:10]
# 输出
[('of--the', 309),
('in--the', 169),
('i--had', 130),
('i--was', 112),
('and--the', 109),
('the--time', 102),
('it--was', 99),
('to--the', 85),
('as--i', 78),
('of--a', 73)]
9.2.6. Summary¶
文本是深度学习中最常见的序列数据形式之一。
构成标记的常见选择是字符、单词和单词片段。
- 为了预处理文本,我们通常
将文本拆分为标记;
构建词汇表以将标记字符串映射到数字索引;
将文本数据转换为标记索引以供模型操作。
在实践中,单词的频率往往遵循齐普夫定律。这不仅适用于单个单词(一元语法),也适用于 n-gram
9.3. Language Models¶
9.3.1. Learning Language Models¶
语言模型的基础公式
例如,包含四个单词的文本序列的概率(联合概率)如下:
9.3.1.1. Markov Models and n-grams¶
- 为了简化计算,语言模型通常假设序列满足马尔可夫性质,即只考虑有限长度的上下文:
Unigram(单词独立):
Bigram(二元组):
Trigram(三元组):
9.3.1.2. Word Frequency¶
在大规模语料库(如Wikipedia或Project Gutenberg)中,词的概率可以通过频率计算:
9.3.1.3. Laplace Smoothing¶
拉普拉斯平滑
- 为了解决低频或未见词组的问题,使用平滑方法在计数中加入小常数
单词概率:
二元组概率:
- 为了解决低频或未见词组的问题,使用平滑方法在计数中加入小常数
尽管平滑方法有效,它依然有局限性,例如高阶组合的稀疏性和存储成本问题。
9.3.2. Perplexity¶
困惑度衡量语言模型对文本预测的好坏:
定义为交叉熵的指数形式:
- 理解:
最优模型:困惑度=1(完美预测)。
随机模型:困惑度接近词汇表大小。
9.3.3. Partitioning Sequences¶
训练语言模型时,将长序列分割成多个子序列,并将输入与目标错开一位。
- 例如:
输入:
目标:
这种分区方式使模型能够学习预测下一个词的能力。
9.4. Recurrent Neural Networks¶
1. 语言模型的局限性与改进¶
- 传统的 n元(n-grams)模型假设一个时间步 t 的词
缺点:如果要捕捉更长的上下文信息,需要增加 n ,但这样参数数量会指数级增长(
- 传统的 n元(n-grams)模型假设一个时间步 t 的词
解决方案:引入隐变量模型,用一个“隐藏状态” h_{t-1} 来存储从 t-1 之前的序列信息:
2. 隐藏状态的定义与作用¶
隐藏状态(hidden state):
好处:相比 n-grams 模型,隐藏状态允许我们在参数不随时间步增加的情况下捕获长程依赖。
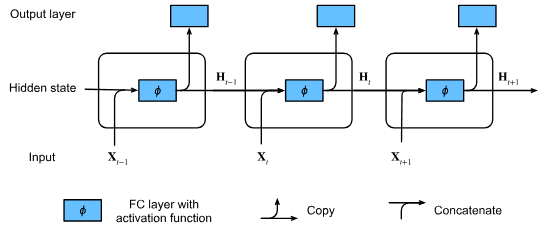
Fig. 9.4.1 An RNN with a hidden state.¶
3. RNN的计算逻辑¶
RNN的隐藏层输出(即隐藏状态)公式:
- 其中
输出层的计算:
- c.特点:
隐藏状态的计算是递归的(recurrent)。
参数(
4. RNN与MLP的区别¶
- MLP(多层感知机):
每个输入样本独立处理,不考虑时间步之间的关联。
隐藏层的输出公式:
- RNN:
利用隐藏状态捕获时间步之间的依赖关系。
隐藏状态递归计算,具备“记忆”能力。
5. RNN的应用¶
- 字符级语言模型(character-level language model):
输入序列(如“machin”)的每个字符作为一个时间步的输入。
输出序列是预测的下一个字符(如“achine”)。
RNN通过隐藏状态捕捉历史上下文信息,并逐步预测下一个字符。
Fig. 9.4.2 A character-level language model based on the RNN. The input and target sequences are “machin” and “achine”, respectively.¶
6. RNN的优点与局限¶
优点:
捕获序列数据的依赖关系。
参数共享,适合处理长序列。
局限:
可能存在梯度消失或梯度爆炸问题,特别是处理长序列时。
为此,通常会改进为LSTM或GRU等变种模型。
总结¶
RNN是一种能够捕获序列信息的神经网络,通过递归计算隐藏状态,实现了对时间序列数据的有效建模。
它的关键思想在于共享模型参数并利用隐藏状态记录序列历史信息,在语言模型等任务中具有广泛的应用。
9.5. Recurrent Neural Network Implementation from Scratch¶
9.5.1. RNN Model¶
class RNNScratch(d2l.Module): #@save
"""The RNN model implemented from scratch."""
def __init__(self, num_inputs, num_hiddens, sigma=0.01):
super().__init__()
self.save_hyperparameters()
self.W_xh = nn.Parameter(
torch.randn(num_inputs, num_hiddens) * sigma)
self.W_hh = nn.Parameter(
torch.randn(num_hiddens, num_hiddens) * sigma)
self.b_h = nn.Parameter(torch.zeros(num_hiddens))
@d2l.add_to_class(RNNScratch) #@save
def forward(self, inputs, state=None):
if state is None:
# Initial state with shape: (batch_size, num_hiddens)
state = torch.zeros((inputs.shape[1], self.num_hiddens),
device=inputs.device)
else:
state, = state
outputs = []
for X in inputs: # Shape of inputs: (num_steps, batch_size, num_inputs)
state = torch.tanh(torch.matmul(X, self.W_xh) +
torch.matmul(state, self.W_hh) + self.b_h)
outputs.append(state)
return outputs, state
应用:
batch_size, num_inputs, num_hiddens, num_steps = 2, 16, 32, 100
rnn = RNNScratch(num_inputs, num_hiddens)
X = torch.ones((num_steps, batch_size, num_inputs))
outputs, state = rnn(X)
def check_len(a, n): #@save
"""Check the length of a list."""
assert len(a) == n, f'list\'s length {len(a)} != expected length {n}'
def check_shape(a, shape): #@save
"""Check the shape of a tensor."""
assert a.shape == shape, \
f'tensor\'s shape {a.shape} != expected shape {shape}'
check_len(outputs, num_steps)
check_shape(outputs[0], (batch_size, num_hiddens))
check_shape(state, (batch_size, num_hiddens))
9.5.2. RNN-Based Language Model¶
class RNNLMScratch(d2l.Classifier): #@save
"""The RNN-based language model implemented from scratch."""
def __init__(self, rnn, vocab_size, lr=0.01):
super().__init__()
self.save_hyperparameters()
self.init_params()
def init_params(self):
self.W_hq = nn.Parameter(
torch.randn(self.rnn.num_hiddens, self.vocab_size) * self.rnn.sigma)
self.b_q = nn.Parameter(torch.zeros(self.vocab_size))
def training_step(self, batch):
l = self.loss(self(*batch[:-1]), batch[-1])
self.plot('ppl', torch.exp(l), train=True)
return l
def validation_step(self, batch):
l = self.loss(self(*batch[:-1]), batch[-1])
self.plot('ppl', torch.exp(l), train=False)
9.5.2.1. One-Hot Encoding¶
示例:
F.one_hot(torch.tensor([0, 2]), 5)
# 输出
tensor([[1, 0, 0, 0, 0],
[0, 0, 1, 0, 0]])
@d2l.add_to_class(RNNLMScratch) #@save
def one_hot(self, X):
# Output shape: (num_steps, batch_size, vocab_size)
return F.one_hot(X.T, self.vocab_size).type(torch.float32)
9.5.2.2. Transforming RNN Outputs¶
@d2l.add_to_class(RNNLMScratch) #@save
def output_layer(self, rnn_outputs):
outputs = [torch.matmul(H, self.W_hq) + self.b_q for H in rnn_outputs]
return torch.stack(outputs, 1)
@d2l.add_to_class(RNNLMScratch) #@save
def forward(self, X, state=None):
embs = self.one_hot(X)
rnn_outputs, _ = self.rnn(embs, state)
return self.output_layer(rnn_outputs)
检查前向计算是否产生具有正确形状的输出:
model = RNNLMScratch(rnn, num_inputs)
outputs = model(torch.ones((batch_size, num_steps), dtype=torch.int64))
check_shape(outputs, (batch_size, num_steps, num_inputs))
9.5.3. Gradient Clipping¶
梯度截断(gradient clipping)
【序列长度与深度】神经网络之所以被称为“深”网络,是因为它们通常有许多层从输入到输出的传递。而在RNN中,由于处理的是时间序列数据,序列的长度引入了一种新的“深度”概念。具体来说,RNN不仅仅是处理输入到输出的网络,它还需要在时间维度上跨越多个时间步长,因此在一个输入序列的前期时间步上的信息必须通过每一个时间步的“层”逐步传递,以影响最终的输出。
【反向传播中的时间维度】在反向传播过程中,梯度是通过时间反向传播的,也就是说,不仅是网络的层之间传递信息,还涉及每个时间步之间的传播。随着时间步数的增加,反向传播需要通过的矩阵乘法链条长度为 T(时间步长),这使得梯度的计算变得更复杂,可能导致数值不稳定。
【梯度剪切(Gradient Clipping)】为了解决梯度爆炸问题,一种常用的“hack”是梯度剪切。梯度剪切通过对梯度进行限制,确保它们的范数不会超过一个设定的最大值
@d2l.add_to_class(d2l.Trainer) #@save
def clip_gradients(self, grad_clip_val, model):
params = [p for p in model.parameters() if p.requires_grad]
norm = torch.sqrt(sum(torch.sum((p.grad ** 2)) for p in params))
if norm > grad_clip_val:
for param in params:
param.grad[:] *= grad_clip_val / norm
9.5.4. Training¶
data = d2l.TimeMachine(batch_size=1024, num_steps=32)
rnn = RNNScratch(num_inputs=len(data.vocab), num_hiddens=32)
model = RNNLMScratch(rnn, vocab_size=len(data.vocab), lr=1)
trainer = d2l.Trainer(max_epochs=100, gradient_clip_val=1, num_gpus=1)
trainer.fit(model, data)
9.5.5. Decoding¶
@d2l.add_to_class(RNNLMScratch) #@save
def predict(self, prefix, num_preds, vocab, device=None):
state, outputs = None, [vocab[prefix[0]]]
for i in range(len(prefix) + num_preds - 1):
X = torch.tensor([[outputs[-1]]], device=device)
embs = self.one_hot(X)
rnn_outputs, state = self.rnn(embs, state)
if i < len(prefix) - 1: # Warm-up period
outputs.append(vocab[prefix[i + 1]])
else: # Predict num_preds steps
Y = self.output_layer(rnn_outputs)
outputs.append(int(Y.argmax(axis=2).reshape(1)))
return ''.join([vocab.idx_to_token[i] for i in outputs])
model.predict('it has', 20, data.vocab, d2l.try_gpu())
# 输出
'it has in the the the the '
9.6. Concise Implementation of Recurrent Neural Networks¶
9.6.1. Defining the Model¶
class RNN(d2l.Module): #@save
"""The RNN model implemented with high-level APIs."""
def __init__(self, num_inputs, num_hiddens):
super().__init__()
self.save_hyperparameters()
self.rnn = nn.RNN(num_inputs, num_hiddens)
def forward(self, inputs, H=None):
return self.rnn(inputs, H)
class RNNLM(d2l.RNNLMScratch): #@save
"""The RNN-based language model implemented with high-level APIs."""
def init_params(self):
self.linear = nn.LazyLinear(self.vocab_size)
def output_layer(self, hiddens):
return self.linear(hiddens).swapaxes(0, 1)
9.6.2. Training and Predicting¶
data = d2l.TimeMachine(batch_size=1024, num_steps=32)
rnn = RNN(num_inputs=len(data.vocab), num_hiddens=32)
model = RNNLM(rnn, vocab_size=len(data.vocab), lr=1)
model.predict('it has', 20, data.vocab)
# 输出
'it hasoadd dd dd dd dd dd '
训练:
trainer = d2l.Trainer(max_epochs=100, gradient_clip_val=1, num_gpus=1)
trainer.fit(model, data)
训练后推理:
model.predict('it has', 20, data.vocab, d2l.try_gpu())
9.7. Backpropagation Through Time¶
时间反向传播(Backpropagation Through Time, BPTT)
应对梯度问题的方法¶
- 全计算(Full Computation):完整计算所有时间步的梯度。
- 缺点:
计算代价高。
容易受到梯度爆炸和数值不稳定的影响。
实际上很少使用。
- 时间步截断(Truncating Time Steps):只计算最近
- 优点:
简化计算,避免梯度爆炸。
偏向短期依赖,有一定正则化效果。
- 缺点:
可能丢失长期依赖的信息。
- 时间步截断(Truncating Time Steps):只计算最近
- 随机截断(Randomized Truncation):用随机变量替代部分梯度计算,以截断序列长度。
- 优点:
截断位置随机化,可能提升训练的泛化能力。
- 缺点:
增加梯度估计的方差,实际效果不显著。
数学分析¶
- 每个时间步的隐藏状态和输出是
f 是隐藏层的变换
g 是输出层的变换
- 前向传播相当简单
通过所有 T 时间步长的目标函数来评估输出
- 反向传播,事情有点棘手
根据链式法则
乘积的第一和第二因子很容易计算。第三个因素
为了导出上述梯度,假设我们有三个序列
由于:
把上面两公式代入一起,即可删除循环计算可得如下公式
总结与实践意义¶
在实际中,时间步截断(Truncated BPTT)是最常用的方法,它在计算效率和模型稳定性之间达成了平衡。
对于处理长序列数据的任务(如文本序列),这种方法既能捕获短期依赖,又能避免梯度问题带来的训练困难。
10. Modern Recurrent Neural Networks¶
10.1. Long Short-Term Memory (LSTM)¶
虽然梯度裁剪有助于梯度爆炸,但处理梯度消失似乎需要更复杂的解决方案。
Hochreiter 和 Schmidhuber (1997) 提出的解决梯度消失问题的第一个也是最成功的技术之一是长短期记忆 (LSTM) 模型。
LSTM 类似于标准的循环神经网络,但这里每个普通的循环节点都被一个记忆单元取代。
每个记忆单元包含一个内部状态,即具有固定权重1的自连接循环边的节点,确保梯度可以跨越许多时间步而不会消失或爆炸。
- “长短期记忆”一词来自以下直觉:
- 简单的循环神经网络具有权重形式的长期记忆。
权重在训练过程中缓慢变化,编码有关数据的一般知识。
它们还具有短暂激活形式的短期记忆,从每个节点传递到连续的节点。
LSTM 模型通过记忆单元引入了中间类型的存储。
存储单元是一个复合单元,由特定连接模式中的简单节点构建而成,并新颖地包含乘法节点。
10.1.1. Gated Memory Cell¶
10.1.1.2. Input Gate, Forget Gate, and Output Gate¶
Fig. 10.1.1 Computing the input gate, the forget gate, and the output gate in an LSTM model.¶
The data feeding into the LSTM gates are the
inputat the current time step and thehidden stateof the previous time stepThe
inputgate determines how much of the input node’s value should be added to the current memory cell internal state.The
forgetgate determines whether to keep the current value of the memory or flush it.The
outputgate determines whether the memory cell should influence the output at the current time step.从数学上讲,假设有 h 个隐藏单元,批量大小为 n ,输入数量为 d
因此,输入是
- Correspondingly, the gates at time step
tare defined as follows: the input gate is
the forget gate is
the output gate is
- Correspondingly, the gates at time step
公式:
where
and
and
10.1.1.3. Input Node¶
公式和上述三个门类似,但使用取值范围为 (-1, 1) 的
tanh函数作为激活函数。
input node :
where
and
Fig. 10.1.2 Computing the input node in an LSTM model.¶
10.1.1.4. Memory Cell Internal State¶
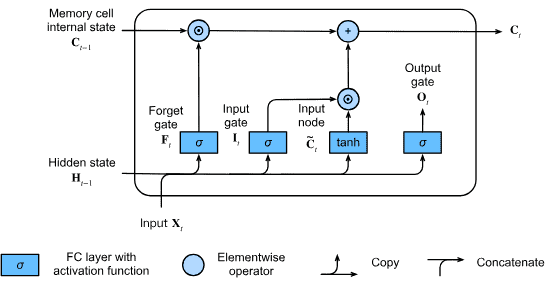
Fig. 10.1.3 Computing the memory cell internal state in an LSTM model.¶
- In LSTMs, the input gate
and the forget gate
- In LSTMs, the input gate
Using the Hadamard (elementwise) product operator
10.1.2. Implementation from Scratch¶
10.1.2.1. Initializing Model Parameters¶
class LSTMScratch(d2l.Module):
def __init__(self, num_inputs, num_hiddens, sigma=0.01):
super().__init__()
self.save_hyperparameters()
init_weight = lambda *shape: nn.Parameter(torch.randn(*shape) * sigma)
triple = lambda: (init_weight(num_inputs, num_hiddens),
init_weight(num_hiddens, num_hiddens),
nn.Parameter(torch.zeros(num_hiddens)))
self.W_xi, self.W_hi, self.b_i = triple() # Input gate
self.W_xf, self.W_hf, self.b_f = triple() # Forget gate
self.W_xo, self.W_ho, self.b_o = triple() # Output gate
self.W_xc, self.W_hc, self.b_c = triple() # Input node
@d2l.add_to_class(LSTMScratch)
def forward(self, inputs, H_C=None):
if H_C is None:
# Initial state with shape: (batch_size, num_hiddens)
H = torch.zeros((inputs.shape[1], self.num_hiddens),
device=inputs.device)
C = torch.zeros((inputs.shape[1], self.num_hiddens),
device=inputs.device)
else:
H, C = H_C
outputs = []
for X in inputs:
I = torch.sigmoid(torch.matmul(X, self.W_xi) +
torch.matmul(H, self.W_hi) + self.b_i)
F = torch.sigmoid(torch.matmul(X, self.W_xf) +
torch.matmul(H, self.W_hf) + self.b_f)
O = torch.sigmoid(torch.matmul(X, self.W_xo) +
torch.matmul(H, self.W_ho) + self.b_o)
C_tilde = torch.tanh(torch.matmul(X, self.W_xc) +
torch.matmul(H, self.W_hc) + self.b_c)
C = F * C + I * C_tilde
H = O * torch.tanh(C)
outputs.append(H)
return outputs, (H, C)
10.1.2.2. Training and Prediction¶
data = d2l.TimeMachine(batch_size=1024, num_steps=32)
lstm = LSTMScratch(num_inputs=len(data.vocab), num_hiddens=32)
model = d2l.RNNLMScratch(lstm, vocab_size=len(data.vocab), lr=4)
trainer = d2l.Trainer(max_epochs=50, gradient_clip_val=1, num_gpus=1)
trainer.fit(model, data)
10.1.3. Concise Implementation¶
class LSTM(d2l.RNN):
def __init__(self, num_inputs, num_hiddens):
d2l.Module.__init__(self)
self.save_hyperparameters()
self.rnn = nn.LSTM(num_inputs, num_hiddens)
def forward(self, inputs, H_C=None):
return self.rnn(inputs, H_C)
lstm = LSTM(num_inputs=len(data.vocab), num_hiddens=32)
model = d2l.RNNLM(lstm, vocab_size=len(data.vocab), lr=4)
trainer.fit(model, data)
使用:
model.predict('it has', 20, data.vocab, d2l.try_gpu())
# 输出
'it has a the time travelly'
10.1.4. Summary¶
LSTM 于 1997 年发布,但在 2000 年代中期的预测竞赛中取得了一些胜利,使其声名鹊起,并从 2011 年开始成为序列学习的主导模型,直到 2017 年开始 Transformer 模型的兴起。
LSTM 具有三种类型的门:输入门、遗忘门和控制信息流的输出门。 LSTM的隐藏层输出包括隐藏状态和记忆单元内部状态。只有隐藏状态被传递到输出层,而存储单元内部状态完全保持在内部。 LSTM 可以缓解梯度消失和爆炸。
10.2. Gated Recurrent Units (GRU)¶
门控循环单元 (GRU)(Cho 等人,2014)提供了 LSTM 存储单元的简化版本,通常可以实现相当的性能,但具有计算速度更快的优点(Chung 等人,2014)。
10.2.1. Reset Gate and Update Gate¶
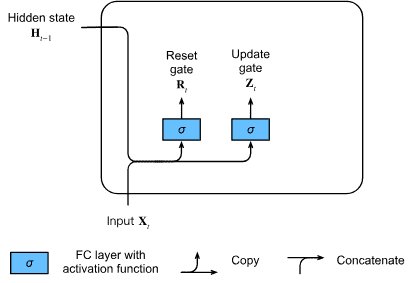
Fig. 10.2.1 Computing the reset gate and the update gate in a GRU model. 给定当前时间步的输入和前一个时间步的隐藏状态。¶
LSTM 的三个门被替换为两个:重置门和更新门。
- 直观上,
重置门控制着我们可能仍想记住多少先前的状态。
更新门将允许我们控制新状态中有多少只是旧状态的副本。
Mathematically, for a given time step
t, suppose that the input is a minibatchnumber of examples =n; number of inputs =d)and the hidden state of the previous time step is
number of hidden units =h).Then the reset gate
10.2.3. Hidden State¶
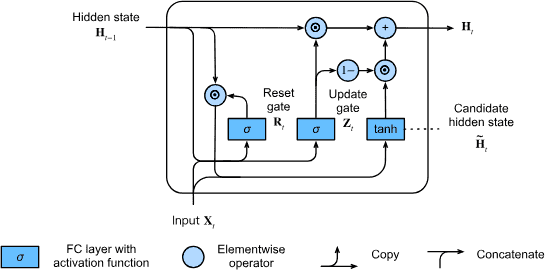
Fig. 10.2.3 Computing the hidden state in a GRU model.¶
每当更新门
相反,每当
- GRU有以下两个显着特征:
Reset gates help capture short-term dependencies in sequences.
Update gates help capture long-term dependencies in sequences.
10.2.4. Implementation from Scratch¶
10.2.4.1. Initializing Model Parameters¶
class GRUScratch(d2l.Module):
def __init__(self, num_inputs, num_hiddens, sigma=0.01):
super().__init__()
self.save_hyperparameters()
init_weight = lambda *shape: nn.Parameter(torch.randn(*shape) * sigma)
triple = lambda: (init_weight(num_inputs, num_hiddens),
init_weight(num_hiddens, num_hiddens),
nn.Parameter(torch.zeros(num_hiddens)))
self.W_xz, self.W_hz, self.b_z = triple() # Update gate
self.W_xr, self.W_hr, self.b_r = triple() # Reset gate
self.W_xh, self.W_hh, self.b_h = triple() # Candidate hidden state
10.2.4.2. Defining the Model¶
@d2l.add_to_class(GRUScratch)
def forward(self, inputs, H=None):
if H is None:
# Initial state with shape: (batch_size, num_hiddens)
H = torch.zeros((inputs.shape[1], self.num_hiddens),
device=inputs.device)
outputs = []
for X in inputs:
Z = torch.sigmoid(torch.matmul(X, self.W_xz) +
torch.matmul(H, self.W_hz) + self.b_z)
R = torch.sigmoid(torch.matmul(X, self.W_xr) +
torch.matmul(H, self.W_hr) + self.b_r)
H_tilde = torch.tanh(torch.matmul(X, self.W_xh) +
torch.matmul(R * H, self.W_hh) + self.b_h)
H = Z * H + (1 - Z) * H_tilde
outputs.append(H)
return outputs, H
10.2.4.3. Training¶
data = d2l.TimeMachine(batch_size=1024, num_steps=32)
gru = GRUScratch(num_inputs=len(data.vocab), num_hiddens=32)
model = d2l.RNNLMScratch(gru, vocab_size=len(data.vocab), lr=4)
trainer = d2l.Trainer(max_epochs=50, gradient_clip_val=1, num_gpus=1)
trainer.fit(model, data)
10.2.5. Concise Implementation¶
class GRU(d2l.RNN):
def __init__(self, num_inputs, num_hiddens):
d2l.Module.__init__(self)
self.save_hyperparameters()
self.rnn = nn.GRU(num_inputs, num_hiddens)
gru = GRU(num_inputs=len(data.vocab), num_hiddens=32)
model = d2l.RNNLM(gru, vocab_size=len(data.vocab), lr=4)
trainer.fit(model, data)
使用:
model.predict('it has', 20, data.vocab, d2l.try_gpu())
# 输出
'it has so it and the time '
10.2.6. Summary¶
与 LSTM 相比,GRU 实现了相似的性能,但计算量往往更轻。
当重置门打开时,GRU 包含基本的 RNN 作为其极端情况。
当更新门打开时,可以用来跳过子序列。
10.3. Deep Recurrent Neural Networks¶
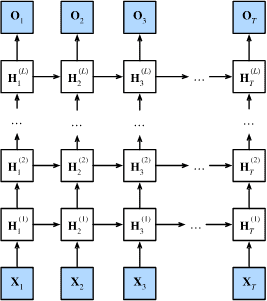
Fig. 10.3.1 Architecture of a deep RNN.¶
the hidden state of the
number of hidden units =h)the output layer variable be
number of outputs: q).Setting
the hidden state of the
最后,输出层的计算仅基于最终
10.3.1. Implementation from Scratch¶
class StackedRNNScratch(d2l.Module):
def __init__(self, num_inputs, num_hiddens, num_layers, sigma=0.01):
super().__init__()
self.save_hyperparameters()
self.rnns = nn.Sequential(*[d2l.RNNScratch(
num_inputs if i==0 else num_hiddens, num_hiddens, sigma)
for i in range(num_layers)])
@d2l.add_to_class(StackedRNNScratch)
def forward(self, inputs, Hs=None):
outputs = inputs
if Hs is None: Hs = [None] * self.num_layers
for i in range(self.num_layers):
outputs, Hs[i] = self.rnns[i](outputs, Hs[i])
outputs = torch.stack(outputs, 0)
return outputs, Hs
使用(为了简单起见,我们将层数设置为 2):
data = d2l.TimeMachine(batch_size=1024, num_steps=32)
rnn_block = StackedRNNScratch(num_inputs=len(data.vocab),
num_hiddens=32, num_layers=2)
model = d2l.RNNLMScratch(rnn_block, vocab_size=len(data.vocab), lr=2)
trainer = d2l.Trainer(max_epochs=100, gradient_clip_val=1, num_gpus=1)
trainer.fit(model, data)
10.3.2. Concise Implementation¶
class GRU(d2l.RNN): #@save
"""The multilayer GRU model."""
def __init__(self, num_inputs, num_hiddens, num_layers, dropout=0):
d2l.Module.__init__(self)
self.save_hyperparameters()
self.rnn = nn.GRU(num_inputs, num_hiddens, num_layers,
dropout=dropout)
gru = GRU(num_inputs=len(data.vocab), num_hiddens=32, num_layers=2)
model = d2l.RNNLM(gru, vocab_size=len(data.vocab), lr=2)
trainer.fit(model, data)
使用:
model.predict('it has', 20, data.vocab, d2l.try_gpu())
# 输出
'it has for and the time th'
10.3.3. Summary¶
在深度 RNN 中,隐藏状态信息被传递到当前层的下一个时间步和下一层的当前时间步。
存在许多不同风格的深度 RNN,例如 LSTM、GRU 或普通 RNN。
10.4. Bidirectional Recurrent Neural Networks¶
将任何单向 RNN 转换为双向 RNN(Schuster 和 Paliwal,1997)。
实现两个单向 RNN 层,它们以相反的方向链接在一起并作用于相同的输入
对于第一个 RNN 层,第一个输入是
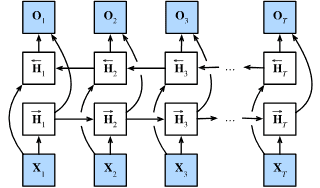
Fig. 10.4.1 Architecture of a bidirectional RNN.¶
前向和后向隐藏状态更新:
最后,输出层计算输出
number of outputs =q):
10.4.1. Implementation from Scratch¶
class BiRNNScratch(d2l.Module):
def __init__(self, num_inputs, num_hiddens, sigma=0.01):
super().__init__()
self.save_hyperparameters()
self.f_rnn = d2l.RNNScratch(num_inputs, num_hiddens, sigma)
self.b_rnn = d2l.RNNScratch(num_inputs, num_hiddens, sigma)
self.num_hiddens *= 2 # The output dimension will be doubled
@d2l.add_to_class(BiRNNScratch)
def forward(self, inputs, Hs=None):
f_H, b_H = Hs if Hs is not None else (None, None)
f_outputs, f_H = self.f_rnn(inputs, f_H)
b_outputs, b_H = self.b_rnn(reversed(inputs), b_H)
outputs = [torch.cat((f, b), -1) for f, b in zip(
f_outputs, reversed(b_outputs))]
return outputs, (f_H, b_H)
10.4.2. Concise Implementation¶
class BiGRU(d2l.RNN):
def __init__(self, num_inputs, num_hiddens):
d2l.Module.__init__(self)
self.save_hyperparameters()
self.rnn = nn.GRU(num_inputs, num_hiddens, bidirectional=True)
self.num_hiddens *= 2
10.4.3. Summary¶
在双向 RNN 中,每个时间步的隐藏状态由当前时间步之前和之后的数据同时确定。
双向 RNN 最适用于序列编码和给定双向上下文的观测值估计。由于梯度链较长,双向 RNN 的训练成本非常高。
10.5. Machine Translation and the Dataset¶
10.5.1. Downloading and Preprocessing the Dataset¶
class MTFraEng(d2l.DataModule): #@save
"""The English-French dataset."""
def _download(self):
d2l.extract(d2l.download(
d2l.DATA_URL+'fra-eng.zip', self.root,
'94646ad1522d915e7b0f9296181140edcf86a4f5'))
with open(self.root + '/fra-eng/fra.txt', encoding='utf-8') as f:
return f.read()
data = MTFraEng()
raw_text = data._download()
print(raw_text[:75])
# 输出
Downloading ../data/fra-eng.zip from http://d2l-data.s3-accelerate.amazonaws.com/fra-eng.zip...
Go. Va !
Hi. Salut !
Run! Cours !
Run! Courez !
Who? Qui ?
Wow! Ça alors !
预处理(用空格替换不间断空格,将大写字母转换为小写字母,以及在单词和标点符号之间插入空格):
@d2l.add_to_class(MTFraEng) #@save
def _preprocess(self, text):
# Replace non-breaking space with space
text = text.replace('\u202f', ' ').replace('\xa0', ' ')
# Insert space between words and punctuation marks
no_space = lambda char, prev_char: char in ',.!?' and prev_char != ' '
out = [' ' + char if i > 0 and no_space(char, text[i - 1]) else char
for i, char in enumerate(text.lower())]
return ''.join(out)
text = data._preprocess(raw_text)
print(text[:80])
# 输出
go . va !
hi . salut !
run ! cours !
run ! courez !
who ? qui ?
wow ! ça alors !
10.5.2. Tokenization¶
src[i] 是源语言(此处为英语)的文本序列中的标记列表, tgt[i] 是目标语言(此处为法语)的标记列表:
@d2l.add_to_class(MTFraEng) #@save
def _tokenize(self, text, max_examples=None):
src, tgt = [], []
for i, line in enumerate(text.split('\n')):
if max_examples and i > max_examples: break
parts = line.split('\t')
if len(parts) == 2:
# Skip empty tokens
src.append([t for t in f'{parts[0]} <eos>'.split(' ') if t])
tgt.append([t for t in f'{parts[1]} <eos>'.split(' ') if t])
return src, tgt
src, tgt = data._tokenize(text)
src[:6], tgt[:6]
# 输出
([['go', '.', '<eos>'],
['hi', '.', '<eos>'],
['run', '!', '<eos>'],
['run', '!', '<eos>'],
['who', '?', '<eos>'],
['wow', '!', '<eos>']],
[['va', '!', '<eos>'],
['salut', '!', '<eos>'],
['cours', '!', '<eos>'],
['courez', '!', '<eos>'],
['qui', '?', '<eos>'],
['ça', 'alors', '!', '<eos>']])
10.5.3. Loading Sequences of Fixed Length¶
@d2l.add_to_class(MTFraEng) #@save
def __init__(self, batch_size, num_steps=9, num_train=512, num_val=128):
super(MTFraEng, self).__init__()
self.save_hyperparameters()
self.arrays, self.src_vocab, self.tgt_vocab = self._build_arrays(
self._download())
@d2l.add_to_class(MTFraEng) #@save
def _build_arrays(self, raw_text, src_vocab=None, tgt_vocab=None):
def _build_array(sentences, vocab, is_tgt=False):
pad_or_trim = lambda seq, t: (
seq[:t] if len(seq) > t else seq + ['<pad>'] * (t - len(seq)))
sentences = [pad_or_trim(s, self.num_steps) for s in sentences]
if is_tgt:
sentences = [['<bos>'] + s for s in sentences]
if vocab is None:
vocab = d2l.Vocab(sentences, min_freq=2)
array = torch.tensor([vocab[s] for s in sentences])
valid_len = (array != vocab['<pad>']).type(torch.int32).sum(1)
return array, vocab, valid_len
src, tgt = self._tokenize(self._preprocess(raw_text),
self.num_train + self.num_val)
src_array, src_vocab, src_valid_len = _build_array(src, src_vocab)
tgt_array, tgt_vocab, _ = _build_array(tgt, tgt_vocab, True)
return ((src_array, tgt_array[:,:-1], src_valid_len, tgt_array[:,1:]),
src_vocab, tgt_vocab)
10.5.4. Reading the Dataset¶
定义 get_dataloader 方法来返回数据迭代器:
@d2l.add_to_class(MTFraEng) #@save
def get_dataloader(self, train):
idx = slice(0, self.num_train) if train else slice(self.num_train, None)
return self.get_tensorloader(self.arrays, train, idx)
读取英语-法语数据集中的第一个小批量:
data = MTFraEng(batch_size=3)
src, tgt, src_valid_len, label = next(iter(data.train_dataloader()))
print('source:', src.type(torch.int32))
print('decoder input:', tgt.type(torch.int32))
print('source len excluding pad:', src_valid_len.type(torch.int32))
print('label:', label.type(torch.int32))
# 输出
source: tensor([
[117, 182, 0, 3, 4, 4, 4, 4, 4],
[ 62, 72, 2, 3, 4, 4, 4, 4, 4],
[ 57, 124, 0, 3, 4, 4, 4, 4, 4]], dtype=torch.int32)
decoder input: tensor([
[ 3, 37, 100, 58, 160, 0, 4, 5, 5],
[ 3, 6, 2, 4, 5, 5, 5, 5, 5],
[ 3, 180, 0, 4, 5, 5, 5, 5, 5]], dtype=torch.int32)
source len excluding pad: tensor([4, 4, 4], dtype=torch.int32)
label: tensor([
[ 37, 100, 58, 160, 0, 4, 5, 5, 5],
[ 6, 2, 4, 5, 5, 5, 5, 5, 5],
[180, 0, 4, 5, 5, 5, 5, 5, 5]], dtype=torch.int32)
@d2l.add_to_class(MTFraEng) #@save
def build(self, src_sentences, tgt_sentences):
raw_text = '\n'.join([src + '\t' + tgt for src, tgt in zip(
src_sentences, tgt_sentences)])
arrays, _, _ = self._build_arrays(
raw_text, self.src_vocab, self.tgt_vocab)
return arrays
src, tgt, _, _ = data.build(['hi .'], ['salut .'])
print('source:', data.src_vocab.to_tokens(src[0].type(torch.int32)))
print('target:', data.tgt_vocab.to_tokens(tgt[0].type(torch.int32)))
# 输出
source: ['hi', '.', '<eos>', '<pad>', '<pad>', '<pad>', '<pad>', '<pad>', '<pad>']
target: ['<bos>', 'salut', '.', '<eos>', '<pad>', '<pad>', '<pad>', '<pad>', '<pad>']
10.5.5. Summary¶
在自然语言处理中,机器翻译是指将源语言中表示文本字符串的序列自动映射到目标语言中表示合理翻译的字符串的任务。
使用单词级标记化,词汇量将明显大于使用字符级标记化,但序列长度会短得多。
为了减轻词汇量过大的影响,我们可以将不常见的标记视为一些“未知”标记。
我们可以截断和填充文本序列,以便所有文本序列都具有相同的长度以小批量加载。
现代实现通常对具有相似长度的序列进行存储,以避免在填充上浪费过多的计算。
10.6. The Encoder–Decoder Architecture¶
在一般的序列到序列问题中,例如机器翻译,输入和输出的长度不同且未对齐。
处理此类数据的标准方法是设计一个编码器-解码器架构
该架构由两个主要组件组成: 将可变长度序列作为输入的编码器,以及解码器充当条件语言模型,接收编码输入和目标序列的左侧上下文,并预测目标序列中的后续标记。
目标:通过将输入序列编码为固定形状的状态,再解码为输出序列,解决输入输出不对齐的问题。

Fig. 10.6.1 The encoder–decoder architecture.¶
10.6.1. Encoder¶
class Encoder(nn.Module): #@save
"""The base encoder interface for the encoder--decoder architecture."""
def __init__(self):
super().__init__()
# Later there can be additional arguments (e.g., length excluding padding)
def forward(self, X, *args):
raise NotImplementedError
- Encoder 接口
功能:接收输入序列(X),并将其转换为固定形状的状态。
方法:forward 或 call,由继承类实现具体逻辑。
10.6.2. Decoder¶
class Decoder(nn.Module): #@save
"""The base decoder interface for the encoder--decoder architecture."""
def __init__(self):
super().__init__()
# Later there can be additional arguments (e.g., length excluding padding)
def init_state(self, enc_all_outputs, *args):
raise NotImplementedError
def forward(self, X, state):
raise NotImplementedError
- Decoder 接口
- 功能:
初始化状态:将编码器的输出转换为解码器的初始状态。
序列生成:基于初始状态和当前输入(如上一步生成的词),逐步生成目标序列。
- 方法:
init_state:初始化状态。
forward 或 call:处理输入并生成输出。
10.6.3. Putting the Encoder and Decoder Together¶
class EncoderDecoder(d2l.Classifier): #@save
"""The base class for the encoder--decoder architecture."""
def __init__(self, encoder, decoder):
super().__init__()
self.encoder = encoder
self.decoder = decoder
def forward(self, enc_X, dec_X, *args):
enc_all_outputs = self.encoder(enc_X, *args)
dec_state = self.decoder.init_state(enc_all_outputs, *args)
# Return decoder output only
return self.decoder(dec_X, dec_state)[0]
10.6.4. Summary¶
编码器-解码器架构可以处理由可变长度序列组成的输入和输出,因此适用于序列到序列的问题,例如机器翻译。
编码器将可变长度序列作为输入,并将其转换为具有固定形状的状态。解码器将固定形状的编码状态映射到可变长度序列。
- 架构的优点
适应性强:适用于任意长度的输入输出序列。
基础性:是后续复杂序列模型(如基于 RNN 的序列模型)的基础。
10.7. Sequence-to-Sequence Learning for Machine Translation¶
在本节中,我们将演示编码器-解码器架构在机器翻译任务中的应用,其中编码器和解码器均实现为 RNN
Fig. 10.7.1 Sequence-to-sequence learning with an RNN encoder and an RNN decoder.¶
特点:输入和输出是长度可变的非对齐序列,例如机器翻译。
- 模型结构:
编码器(Encoder):RNN(如GRU)将可变长度的输入序列压缩为固定形状的隐藏状态,称为上下文变量(context variable)。
解码器(Decoder):RNN从编码器生成的上下文变量和先前输出的目标序列中,逐步预测下一个输出标记。
注意机制的预告:未来章节会引入注意力机制,可以避免将整个输入压缩为固定长度,增强模型性能。
10.7.1. Teacher Forcing¶
- 训练方法:Teacher Forcing
解码器的输入为真实目标序列(即“ground truth”)的偏移版本,例如:<bos>、”Ils”、”regardent”、”.” 对应 “Ils”、”regardent”、”.”、<eos>。
通过这种方式,解码器始终以正确的先前标记作为输入,帮助模型更快收敛。
10.7.2. Encoder¶
- 接受输入序列,将每个时间步的特征向量(
即:
- 接受输入序列,将每个时间步的特征向量(
- 上下文变量可以是最后一个时间步的隐藏状态,或者经过自定义函数处理的所有隐藏状态。
编码器通过自定义函数 q 将所有时间步的隐藏状态转换为上下文变量
可以使用单向或双向RNN,双向RNN可以捕获更多序列信息。
def init_seq2seq(module): #@save
"""Initialize weights for sequence-to-sequence learning."""
if type(module) == nn.Linear:
nn.init.xavier_uniform_(module.weight)
if type(module) == nn.GRU:
for param in module._flat_weights_names:
if "weight" in param:
nn.init.xavier_uniform_(module._parameters[param])
class Seq2SeqEncoder(d2l.Encoder): #@save
"""The RNN encoder for sequence-to-sequence learning."""
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers, dropout=0):
super().__init__()
self.embedding = nn.Embedding(vocab_size, embed_size)
self.rnn = d2l.GRU(embed_size, num_hiddens, num_layers, dropout)
self.apply(init_seq2seq)
def forward(self, X, *args):
# X shape: (batch_size, num_steps)
embs = self.embedding(X.t().type(torch.int64))
# embs shape: (num_steps, batch_size, embed_size)
outputs, state = self.rnn(embs)
# outputs shape: (num_steps, batch_size, num_hiddens)
# state shape: (num_layers, batch_size, num_hiddens)
return outputs, state
实例化一个两层 GRU 编码器,其隐藏单元数为 16。给定一个小批量序列输入 X (批量大小 =4 ;时间步数 =9 )是一个形状张量(时间步数、批量大小、隐藏层数)单位):
vocab_size, embed_size, num_hiddens, num_layers = 10, 8, 16, 2
batch_size, num_steps = 4, 9
encoder = Seq2SeqEncoder(vocab_size, embed_size, num_hiddens, num_layers)
X = torch.zeros((batch_size, num_steps))
enc_outputs, enc_state = encoder(X)
d2l.check_shape(enc_outputs, (num_steps, batch_size, num_hiddens))
10.7.3. Decoder¶
- 输入包括先前时间步的输出序列(
用一个函数 g() 来表达解码器隐藏层的变换
- 输入包括先前时间步的输出序列(
计算出新的隐藏状态后,通过softmax计算输出标记
通常,解码器的初始隐藏状态由编码器的最终隐藏状态初始化。
class Seq2SeqDecoder(d2l.Decoder):
"""The RNN decoder for sequence to sequence learning."""
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
dropout=0):
super().__init__()
self.embedding = nn.Embedding(vocab_size, embed_size)
self.rnn = d2l.GRU(embed_size+num_hiddens, num_hiddens, num_layers, dropout)
self.dense = nn.LazyLinear(vocab_size)
self.apply(init_seq2seq)
def init_state(self, enc_all_outputs, *args):
return enc_all_outputs
def forward(self, X, state):
# X shape: (batch_size, num_steps)
# embs shape: (num_steps, batch_size, embed_size)
embs = self.embedding(X.t().type(torch.int32))
enc_output, hidden_state = state
# context shape: (batch_size, num_hiddens)
context = enc_output[-1]
# Broadcast context to (num_steps, batch_size, num_hiddens)
context = context.repeat(embs.shape[0], 1, 1)
# Concat at the feature dimension
embs_and_context = torch.cat((embs, context), -1)
outputs, hidden_state = self.rnn(embs_and_context, hidden_state)
outputs = self.dense(outputs).swapaxes(0, 1)
# outputs shape: (batch_size, num_steps, vocab_size)
# hidden_state shape: (num_layers, batch_size, num_hiddens)
return outputs, [enc_output, hidden_state]
解码器的输出形状变为(批量大小、时间步数、词汇大小),其中张量的最终维度存储预测的标记分布:
decoder = Seq2SeqDecoder(vocab_size, embed_size, num_hiddens, num_layers)
state = decoder.init_state(encoder(X))
dec_outputs, state = decoder(X, state)
d2l.check_shape(dec_outputs, (batch_size, num_steps, vocab_size))
d2l.check_shape(state[1], (num_layers, batch_size, num_hiddens))
Fig. 10.7.2 Layers in an RNN encoder–decoder model.¶
10.7.4. Encoder–Decoder for Sequence-to-Sequence Learning¶
class Seq2Seq(d2l.EncoderDecoder): #@save
"""The RNN encoder--decoder for sequence to sequence learning."""
def __init__(self, encoder, decoder, tgt_pad, lr):
super().__init__(encoder, decoder)
self.save_hyperparameters()
def validation_step(self, batch):
Y_hat = self(*batch[:-1])
self.plot('loss', self.loss(Y_hat, batch[-1]), train=False)
def configure_optimizers(self):
# Adam optimizer is used here
return torch.optim.Adam(self.parameters(), lr=self.lr)
10.7.5. Loss Function with Masking¶
@d2l.add_to_class(Seq2Seq)
def loss(self, Y_hat, Y):
l = super(Seq2Seq, self).loss(Y_hat, Y, averaged=False)
mask = (Y.reshape(-1) != self.tgt_pad).type(torch.float32)
return (l * mask).sum() / mask.sum()
使用交叉熵损失函数,排除填充标记(padding tokens)的计算以避免对模型优化的干扰。
掩码机制通过将无关位置设置为零实现。
10.7.6. Training¶
data = d2l.MTFraEng(batch_size=128)
embed_size, num_hiddens, num_layers, dropout = 256, 256, 2, 0.2
encoder = Seq2SeqEncoder(
len(data.src_vocab), embed_size, num_hiddens, num_layers, dropout)
decoder = Seq2SeqDecoder(
len(data.tgt_vocab), embed_size, num_hiddens, num_layers, dropout)
model = Seq2Seq(encoder, decoder, tgt_pad=data.tgt_vocab['<pad>'],
lr=0.005)
trainer = d2l.Trainer(max_epochs=30, gradient_clip_val=1, num_gpus=1)
trainer.fit(model, data)
10.7.7. Prediction¶
Fig. 10.7.3 Predicting the output sequence token by token using an RNN encoder–decoder.¶
- 预测方法
解码器在测试时基于已预测的标记作为输入逐步生成输出,直到预测到结束标记<eos>。
流程如图所示,逐个标记预测,直到序列结束。
@d2l.add_to_class(d2l.EncoderDecoder) #@save
def predict_step(self, batch, device, num_steps, save_attention_weights=False):
batch = [a.to(device) for a in batch]
src, tgt, src_valid_len, _ = batch
enc_all_outputs = self.encoder(src, src_valid_len)
dec_state = self.decoder.init_state(enc_all_outputs, src_valid_len)
outputs, attention_weights = [tgt[:, (0)].unsqueeze(1), ], []
for _ in range(num_steps):
Y, dec_state = self.decoder(outputs[-1], dec_state)
outputs.append(Y.argmax(2))
# Save attention weights (to be covered later)
if save_attention_weights:
attention_weights.append(self.decoder.attention_weights)
return torch.cat(outputs[1:], 1), attention_weights
10.7.8. Evaluation of Predicted Sequences¶
- BLEU: Bilingual Evaluation Understudy
测量预测序列与目标序列之间的匹配度,基于 n-gram 的精确度计算。
- 权重机制:
匹配更长的 n-gram 赋予更高权重。
短序列惩罚项防止模型生成过短的结果。
def bleu(pred_seq, label_seq, k): #@save
"""Compute the BLEU."""
pred_tokens, label_tokens = pred_seq.split(' '), label_seq.split(' ')
len_pred, len_label = len(pred_tokens), len(label_tokens)
score = math.exp(min(0, 1 - len_label / len_pred))
for n in range(1, min(k, len_pred) + 1):
num_matches, label_subs = 0, collections.defaultdict(int)
for i in range(len_label - n + 1):
label_subs[' '.join(label_tokens[i: i + n])] += 1
for i in range(len_pred - n + 1):
if label_subs[' '.join(pred_tokens[i: i + n])] > 0:
num_matches += 1
label_subs[' '.join(pred_tokens[i: i + n])] -= 1
score *= math.pow(num_matches / (len_pred - n + 1), math.pow(0.5, n))
return score
示例:
engs = ['go .', 'i lost .', 'he\'s calm .', 'i\'m home .']
fras = ['va !', 'j\'ai perdu .', 'il est calme .', 'je suis chez moi .']
preds, _ = model.predict_step(
data.build(engs, fras), d2l.try_gpu(), data.num_steps)
for en, fr, p in zip(engs, fras, preds):
translation = []
for token in data.tgt_vocab.to_tokens(p):
if token == '<eos>':
break
translation.append(token)
print(f'{en} => {translation}, bleu,'
f'{bleu(" ".join(translation), fr, k=2):.3f}')
# 输出
go . => ['va', '!'], bleu,1.000
i lost . => ["j'ai", 'perdu', '.'], bleu,1.000
he's calm . => ['elle', 'court', '.'], bleu,0.000
i'm home . => ['je', 'suis', 'chez', 'moi', '.'], bleu,1.000
10.8. Beam Search¶
在序列生成任务中使用的三种搜索策略:贪婪搜索(Greedy Search)、穷举搜索(Exhaustive Search)和束搜索(Beam Search)。
前面章节只提到了贪婪策略
10.8.1. Greedy Search¶
在任何时间步骤 t’ ,我们只需从 y 中选择条件概率最高的标记

Fig. 10.8.1 At each time step, greedy search selects the token with the highest conditional probability.¶
在每个时间步,贪婪搜索都会选择条件概率最高的标记。因此,将预测输出序列“A”、“B”、“C”和“”(图10.8.1)。该输出序列的条件概率为

Fig. 10.8.2 The four numbers under each time step represent the conditional probabilities of generating “A”, “B”, “C”, and “<eos>” at that time step. At time step 2, the token “C”, which has the second highest conditional probability, is selected.¶
输出序列“A”、“C”、“B”、“”的条件概率为
10.8.2. Exhaustive Search¶
枚举所有可能的输出序列及其条件概率,然后输出预测概率最高的序列。
它会带来令人望而却步的计算成本
例如,当
另一方面,贪婪搜索的计算成本是
例如,当
10.8.3. Beam Search¶
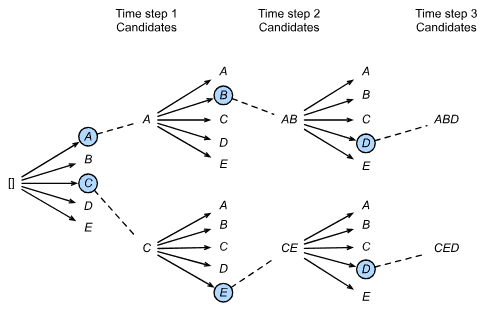
Fig. 10.8.3 The process of beam search (beam size =2; maximum length of an output sequence =3). The candidate output sequences are A, C, AB, CE, ABD, and CED.¶
集束搜索的计算成本为
11. Attention Mechanisms and Transformers¶
11.1. Queries, Keys, and Values¶
【1. 传统网络的局限性(Fixed Input Size)】最初的神经网络(如CNN、RNN等)依赖于输入的大小是固定的,比如ImageNet中的图像大小是
- 【2. 数据库类比(Databases and Key-Value Pairs)】数据库通常包含由
键(k)和值(v)组成的键值对。 例如,假设有一组姓氏和名字的键值对。如果我们查询某个特定的键(如“Li”),我们会得到相应的值(“Mu”)。这里的
查询(q)可以返回一个结果,也可以返回多个近似结果,具体取决于数据库中的内容。- 重要的概念:
查询可以不依赖于数据库的大小,这表明深度学习模型可以扩展到较大的数据集。
查询可以得到不同的答案,这与深度学习中的模型预测类似。
操作不需要对数据库进行复杂的压缩或简化。
- 【2. 数据库类比(Databases and Key-Value Pairs)】数据库通常包含由
【3. 引入注意力机制(Attention Mechanism)】随着深度学习的发展,注意力机制作为一个非常有用的工具被引入。它模拟了查询与一组键值对之间的关系,允许模型在进行决策时重点关注重要的键(
k)及其对应的值(v)。具体来说,注意力机制定义如下:
这里的
- 【4. 不同的权重分配方法(Weighting Mechanisms)】几种常见的权重分配方式:
非负权重:权重
归一化权重:权重
精确匹配:只有一个权重为1,其余为0,这类似于传统的数据库查询。
平均池化:所有权重相等,这相当于对整个数据库进行平均池化。
Fig. 11.1.1 The attention mechanism computes a linear combination over values
11.1.1. Visualization¶
注意力机制的一个优势是其直观性,尤其是在权重为非负并且总和为1时。
通过观察注意力权重的分布,我们可以理解哪些部分对模型的预测最为重要。
#@save
def show_heatmaps(matrices, xlabel, ylabel, titles=None, figsize=(2.5, 2.5),
cmap='Reds'):
"""Show heatmaps of matrices."""
d2l.use_svg_display()
num_rows, num_cols, _, _ = matrices.shape
fig, axes = d2l.plt.subplots(num_rows, num_cols, figsize=figsize,
sharex=True, sharey=True, squeeze=False)
for i, (row_axes, row_matrices) in enumerate(zip(axes, matrices)):
for j, (ax, matrix) in enumerate(zip(row_axes, row_matrices)):
pcm = ax.imshow(matrix.detach().numpy(), cmap=cmap)
if i == num_rows - 1:
ax.set_xlabel(xlabel)
if j == 0:
ax.set_ylabel(ylabel)
if titles:
ax.set_title(titles[j])
fig.colorbar(pcm, ax=axes, shrink=0.6);
使用:
attention_weights = torch.eye(10).reshape((1, 1, 10, 10))
show_heatmaps(attention_weights, xlabel='Keys', ylabel='Queries')
11.1.2. Summary¶
到目前为止,我们的讨论非常抽象,只是描述了一种池化数据的方法。
我们还没有解释这些神秘的查询、键和值可能从何而来。
一些直觉可能会有所帮助:例如,在回归设置中,查询可能对应于应执行回归的位置。键是观察过去数据的位置,值是(回归)值本身。
11.2. Attention Pooling by Similarity¶
Nadaraya–Watson estimators的核心依赖于一些将查询 q 与键 k 相关联的相似性内核
一些常见的内核:
核心点-fromGPT¶
核心概念¶
【Nadaraya-Watson 核回归】:统计学方法,用于回归和分类任务。该方法通过查询点与训练数据点之间的相似度(或核函数)来计算预测值。
【核函数】:核函数是计算两个点(查询点和键)之间相似度的函数。高斯核给出一个平滑的、随着距离增加而衰减的相似度,而 Boxcar 核仅对在某个特定范围内的点赋予非零相似度,Epanechikov 核的效果类似,但它的截断更加柔和。
【与注意力机制的联系】:在机器学习模型中,特别是深度学习中,注意力机制的工作方式与此相似:它根据不同输入对当前任务的相关性赋予不同的权重。在这里,”查询”是我们想要进行预测的点,”键”是训练数据点。每个训练点的注意力权重是通过查询点与训练点的相似度来计算的,这与 Nadaraya-Watson 回归中的核函数计算方式类似。
关键见解¶
无需训练: Nadaraya-Watson 回归不需要像传统机器学习模型那样进行训练,模型通过计算查询点与训练数据点的相似度来直接做出预测。这是一种简单的、非参数化的方法,与需要学习参数的复杂神经网络模型有所不同。
核函数的可调性: 核函数的宽度(尤其是高斯核)对估计函数的平滑度有重要影响。更窄的核函数会导致估计结果更加敏感于局部变化,而更宽的核函数则会平滑掉噪声。
关键总结¶
早期的注意力机制: Nadaraya-Watson 回归方法是现代注意力机制的前身之一,展示了如何基于数据点之间的相似性进行加权预测。
简单有效的估计: 这种方法是一种简单的非参数方法,适用于回归和分类任务,尤其在数据丰富时特别有效。
核函数的选择: 核函数的选择,尤其是核函数宽度的设置,能显著影响模型的表现。这与现代注意力机制对注意力函数结构的敏感性类似。
为什么重要¶
这一部分非常重要,因为它将经典的统计学方法与现代深度学习中的注意力机制联系起来。通过了解注意力机制的简单起源,读者可以更清楚地理解为什么注意力机制在深度学习中如此关键,并能够理解其演化过程。
11.2.1. Kernels and Data¶
本节中定义的所有内核
# Define some kernels
def gaussian(x):
return torch.exp(-x**2 / 2)
def boxcar(x):
return torch.abs(x) < 1.0
def constant(x):
return 1.0 + 0 * x
def epanechikov(x):
return torch.max(1 - torch.abs(x), torch.zeros_like(x))
fig, axes = d2l.plt.subplots(1, 4, sharey=True, figsize=(12, 3))
kernels = (gaussian, boxcar, constant, epanechikov)
names = ('Gaussian', 'Boxcar', 'Constant', 'Epanechikov')
x = torch.arange(-2.5, 2.5, 0.1)
for kernel, name, ax in zip(kernels, names, axes):
ax.plot(x.detach().numpy(), kernel(x).detach().numpy())
ax.set_xlabel(name)
d2l.plt.show()
11.2.2. Attention Pooling via Nadaraya–Watson Regression¶
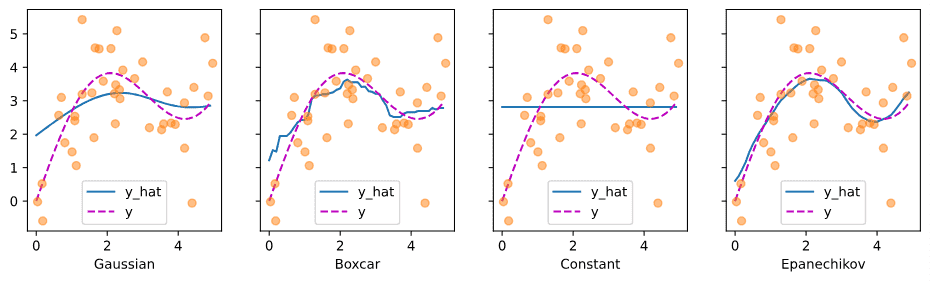
三个非平凡核(Gaussian、Boxcar 和 Epanechikov)都会产生相当可行的估计,与真实函数相差不远。¶
11.2.3. Adapting Attention Pooling¶
用不同宽度的核替换高斯核。也就是说,我们可以使用
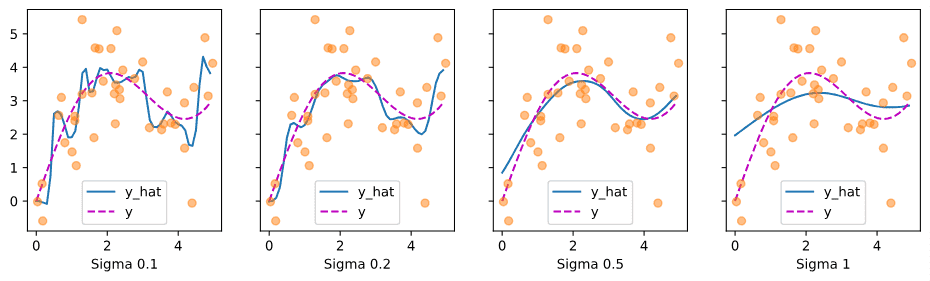
核越窄,估计就越不平滑。同时,它能更好地适应当地的变化。¶
11.2.4. Summary¶
学习这个半个多世纪历史的方法的原因:首先,它是现代注意力机制最早的先驱之一。其次,它非常适合可视化。第三,同样重要的是,它展示了手工注意力机制的局限性。更好的策略是通过学习查询和键的表示来学习该机制。
Nadaraya – Watson内核回归是当前注意机制的早期起源。它可以直接使用,几乎没有培训或调整,无论是用于分类还是回归。注意力的重量是根据查询和钥匙之间的相似性(或距离)分配的,并且根据有多少相似观察结果。
11.3. Attention Scoring Functions¶
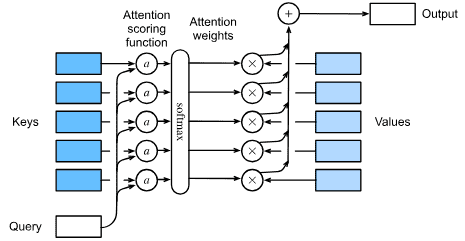
Computing the output of attention pooling as a weighted average of values, where weights are computed with the attention scoring function
核心点-fromGPT¶
注意力评分函数(attention scoring functions)是计算注意力权重的核心函数,通常用于加权求和输入的值(values),从而产生输出。
两种常见的评分函数:点积注意力(Dot Product Attention)和加法注意力(Additive Attention)
11.3.1. Dot Product Attention¶
高斯内核(Gaussian kernel)的注意力评分函数
点积注意力是最常用的注意力机制之一,广泛应用于现代的Transformer架构。核心思想是通过计算查询(query)与键(key)之间的点积来评估它们的相似性。这个相似性得分再通过softmax函数归一化,得到注意力权重。
然后,通过变形公式简化得到点积注意力的公式:
其中,d 是查询向量和键向量的维度。这个公式表明,点积注意力的核心是计算查询和键的标准化点积。
最终,得到的注意力权重
这样做的好处是,可以保证所有的注意力权重是非负的,并且它们的和为1,确保了后续加权求和时的稳定性。
11.3.2. Convenience Functions¶
11.3.2.1. Masked Softmax Operation¶
在序列模型中,常常需要处理不同长度的序列。在这种情况下,我们需要掩蔽操作来忽略填充(padding)部分对注意力计算的影响。
例如,如果一个批次中有三个句子,其中一个句子较短,包含填充符 <blank>,我们需要确保这些填充部分不会影响最终的注意力计算。掩蔽操作通过将填充部分的注意力权重设置为非常小的负数(如
11.3.2.2. Batch Matrix Multiplication¶
在实际应用中,通常会处理多个查询、键和值,因此需要对多个矩阵进行批量矩阵乘法(BMM)。BMM 是一种高效的操作,可以在一个步骤中同时计算多个查询与键的点积。
公式如下:
11.3.3. Scaled Dot Product Attention¶
为了控制点积值的规模,通常使用“缩放”操作,将点积结果除以查询和键的维度的平方根
这种缩放有助于避免随着向量维度增加,点积值变得过大,导致梯度不稳定的问题。
11.3.4. Additive Attention¶
当查询向量和键向量的维度不一致时,可以使用加法注意力。加法注意力通过将查询和键向量结合(例如,使用一个权重矩阵)进行变换,之后再使用一个激活函数(通常是tanh)计算评分。
其评分函数为:
其中
最后,通过softmax对得分进行归一化,得到最终的注意力权重。
11.4. The Bahdanau Attention Mechanism¶
在第10.7节中遇到机器翻译时,我们设计了一个基于两个RNN的序列到序列学习的 encoder–decoder 体系结构(Sutskever等,2014)。具体而言,RNN编码器将变量长度序列转换为固定形状上下文变量。然后,RNN解码器基于生成的令牌和上下文变量生成输出(目标)序列令牌。
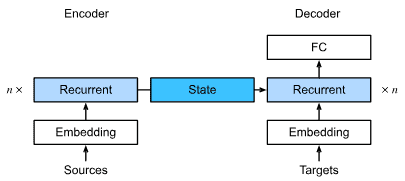
Fig. 11.4.1 Sequence-to-sequence model. The state, as generated by the encoder, is the only piece of information shared between the encoder and the decoder.¶
这对于简短序列来说是很合理的,但很明显,对于长篇小说,例如章节甚至是很长的句子都是不可行的。毕竟,不久之后,中间表示中根本没有足够的“空间”来存储所有重要的内容。因此,解码器将无法翻译长而复杂的句子。
核心点-fromGPT¶
【定义】Bahdanau Attention Mechanism:是一个在序列到序列(sequence-to-sequence, seq2seq)模型中使用的注意力机制,它能够根据输入序列的不同部分选择性地聚焦(“注意”)最相关的信息,特别是在长序列的情况下。
关键点分析¶
背景(Sequence-to-Sequence模型):在经典的seq2seq模型中,使用了两个RNN,一个是编码器(encoder),将输入序列编码成一个固定维度的状态变量;另一个是解码器(decoder),根据编码器的输出生成目标序列。这个固定维度的状态变量通常无法很好地处理长序列,因为它将整个输入序列压缩成一个向量,导致信息丢失。因此,模型对长句子的翻译效果较差。
Bahdanau Attention机制: 问题 : 当输入序列较长时,传统的seq2seq模型中的固定状态(context variable)无法包含足够的信息,导致解码器无法准确生成目标序列。 解决方案 : Bahdanau Attention机制提出了在解码时,不是依赖固定的上下文向量,而是根据当前解码器的状态(即上一时刻的隐藏状态)动态选择输入序列中最相关的部分。具体来说,解码器每次生成一个新token时,会基于当前的解码器状态(上一时刻的隐藏状态)作为查询(query),在编码器的所有隐藏状态中计算注意力权重,选择最相关的部分来更新上下文向量。这个上下文向量(context variable)然后用于生成下一个token。
关键概念¶
注意力机制(Attention Mechanism):通过动态计算和聚焦在输入的不同部分,让模型能够根据当前需要的信息来生成输出,而不是依赖一个固定的上下文向量。
加性注意力(Additive Attention):通过计算当前查询和所有键之间的相关性,生成权重并对值进行加权求和,以此来动态调整上下文。
动态上下文(Dynamic Context):不是使用固定的上下文,而是根据解码器的当前状态和编码器的输出动态更新上下文向量。
11.4.1. Model¶
context variable
encoder hidden states
decoder hidden states
The key idea is that instead of keeping the state, i.e., the
context variablesummarizing the source sentence, as fixed, we dynamically update it, as a function of both the original text (encoder hidden states) and the text that was already generated (decoder hidden states).This yields
We used
Note that
In particular, the attention weight
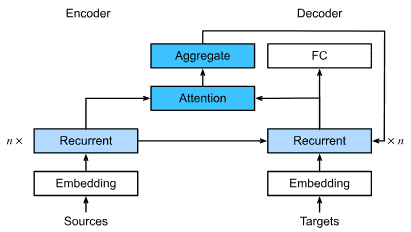
Fig. 11.4.2 Layers in an RNN encoder–decoder model with the Bahdanau attention mechanism.¶
11.4.2. Defining the Decoder with Attention¶
class AttentionDecoder(d2l.Decoder): #@save
"""The base attention-based decoder interface."""
def __init__(self):
super().__init__()
@property
def attention_weights(self):
raise NotImplementedError
class Seq2SeqAttentionDecoder(AttentionDecoder):
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers, dropout=0):
super().__init__()
self.attention = d2l.AdditiveAttention(num_hiddens, dropout)
self.embedding = nn.Embedding(vocab_size, embed_size)
self.rnn = nn.GRU(embed_size + num_hiddens, num_hiddens, num_layers, dropout=dropout)
self.dense = nn.LazyLinear(vocab_size)
self.apply(d2l.init_seq2seq)
def init_state(self, enc_outputs, enc_valid_lens):
# Shape of outputs: (num_steps, batch_size, num_hiddens).
# Shape of hidden_state: (num_layers, batch_size, num_hiddens)
outputs, hidden_state = enc_outputs
return (outputs.permute(1, 0, 2), hidden_state, enc_valid_lens)
def forward(self, X, state):
# Shape of enc_outputs: (batch_size, num_steps, num_hiddens).
# Shape of hidden_state: (num_layers, batch_size, num_hiddens)
enc_outputs, hidden_state, enc_valid_lens = state
# Shape of the output X: (num_steps, batch_size, embed_size)
X = self.embedding(X).permute(1, 0, 2)
outputs, self._attention_weights = [], []
for x in X:
# Shape of query: (batch_size, 1, num_hiddens)
query = torch.unsqueeze(hidden_state[-1], dim=1)
# Shape of context: (batch_size, 1, num_hiddens)
context = self.attention(query, enc_outputs, enc_outputs, enc_valid_lens)
# Concatenate on the feature dimension
x = torch.cat((context, torch.unsqueeze(x, dim=1)), dim=-1)
# Reshape x as (1, batch_size, embed_size + num_hiddens)
out, hidden_state = self.rnn(x.permute(1, 0, 2), hidden_state)
outputs.append(out)
self._attention_weights.append(self.attention.attention_weights)
# After fully connected layer transformation, shape of outputs:
# (num_steps, batch_size, vocab_size)
outputs = self.dense(torch.cat(outputs, dim=0))
return outputs.permute(1, 0, 2), [enc_outputs, hidden_state, enc_valid_lens]
@property
def attention_weights(self):
return self._attention_weights
使用四个序列的小匹配来测试实现的解码器,每个序列长七个时间步长:
vocab_size, embed_size, num_hiddens, num_layers = 10, 8, 16, 2
batch_size, num_steps = 4, 7
encoder = d2l.Seq2SeqEncoder(vocab_size, embed_size, num_hiddens, num_layers)
decoder = Seq2SeqAttentionDecoder(vocab_size, embed_size, num_hiddens, num_layers)
X = torch.zeros((batch_size, num_steps), dtype=torch.long)
state = decoder.init_state(encoder(X), None)
output, state = decoder(X, state)
d2l.check_shape(output, (batch_size, num_steps, vocab_size))
d2l.check_shape(state[0], (batch_size, num_steps, num_hiddens))
d2l.check_shape(state[1][0], (batch_size, num_hiddens))
11.4.3. Training¶
指定超参数,实例化常规编码器和引起注意的解码器,然后将此模型训练以进行机器翻译:
data = d2l.MTFraEng(batch_size=128)
embed_size, num_hiddens, num_layers, dropout = 256, 256, 2, 0.2
encoder = d2l.Seq2SeqEncoder(len(data.src_vocab), embed_size, num_hiddens, num_layers, dropout)
decoder = Seq2SeqAttentionDecoder(len(data.tgt_vocab), embed_size, num_hiddens, num_layers, dropout)
model = d2l.Seq2Seq(encoder, decoder, tgt_pad=data.tgt_vocab['<pad>'], lr=0.005)
trainer = d2l.Trainer(max_epochs=30, gradient_clip_val=1, num_gpus=1)
trainer.fit(model, data)
将一些英语句子翻译成法语并计算其BLEU分数:
engs = ['go .', 'i lost .', 'he\'s calm .', 'i\'m home .']
fras = ['va !', 'j\'ai perdu .', 'il est calme .', 'je suis chez moi .']
preds, _ = model.predict_step(
data.build(engs, fras), d2l.try_gpu(), data.num_steps)
for en, fr, p in zip(engs, fras, preds):
translation = []
for token in data.tgt_vocab.to_tokens(p):
if token == '<eos>':
break
translation.append(token)
print(f'{en} => {translation}, bleu,'
f'{d2l.bleu(" ".join(translation), fr, k=2):.3f}')
# 输出
go . => ['va', '!'], bleu,1.000
i lost . => ["j'ai", 'perdu', '.'], bleu,1.000
he's calm . => ['il', 'court', '.'], bleu,0.000
i'm home . => ['je', 'suis', 'chez', 'moi', '.'], bleu,1.000
11.4.4. Summary¶
Bahdanau Attention机制的核心思想是在生成每个token时,解码器不再只依赖一个固定的上下文向量,而是通过注意力机制动态地选择和聚焦在输入序列的最相关部分。这使得模型能够更好地处理长序列,避免了传统seq2seq模型在处理长文本时遇到的瓶颈。
11.5. Multi-Head Attention¶
在实践中,给定相同的查询,键和值,我们可能希望我们的模型结合相同注意力机制的不同行为的知识,例如捕获各种范围的依赖性(例如,较短范围与较长范围)在序列中。因此,允许我们的注意机制共同使用查询,键和值的不同表示子空间可能是有益的。
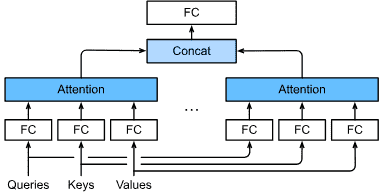
Fig. 11.5.1 Multi-head attention, where multiple heads are concatenated then linearly transformed.¶
FC: fully connected layers
核心点-fromGPT¶
关键点分析¶
【背景和动机】:单头注意力机制通常用于从查询(query)、键(key)和值(value)中计算注意力。在实践中,我们可能希望模型能够从同一注意力机制中获得不同的行为表现,比如捕捉不同范围的依赖关系(例如,短程依赖和长程依赖)。为了实现这一目标,Multi-Head Attention机制让模型能够在多个子空间中并行计算不同的注意力,以便捕捉更多的信息。每个头(head)独立处理一个注意力池化过程,并且可以关注输入序列的不同部分。
【多头注意力的优势】:每个头可以关注输入的不同部分,从而能够捕捉到不同的信息,特别是在处理复杂的、长序列时,它能够有效地捕获不同的依赖关系。通过并行计算多个头,模型可以高效地同时学习多个表示子空间的信息,增强模型的表达能力。
【实现中的优化】:在实际实现中,选择缩放点积注意力(scaled dot product attention)作为每个头的注意力函数,以避免计算成本和参数量的剧烈增长。为了保证计算的高效性,查询、键和值的输出维度通常会设置为
关键概念¶
注意力头(Attention Head):每个头独立计算一个注意力过程,关注输入序列的不同部分,最终将多个头的输出进行拼接并线性变换得到最终的结果。
多头注意力(Multi-Head Attention):通过多个头的并行计算,可以在不同的子空间中学习到更多的信息,提高模型的表示能力。
缩放点积注意力(Scaled Dot Product Attention):通常用于每个头的注意力计算,采用点积方式,并通过缩放因子来避免点积过大导致梯度消失的问题。
11.5.1. Model¶
【具体实现】:在多头注意力中,首先通过对查询、键和值进行线性变换,将它们映射到不同的子空间(这一步通过h个不同的线性变换实现),每个头会得到一个独立的查询、键和值。之后,将这些头的结果并行计算注意力。
query:
key:
value:
attention head:
计算过程的公式
其中
最终的多头注意力输出是将所有头的输出拼接在一起后,再通过一个线性变换生成:
11.5.2. Implementation¶
class MultiHeadAttention(d2l.Module): #@save
"""Multi-head attention."""
def __init__(self, num_hiddens, num_heads, dropout, bias=False, **kwargs):
super().__init__()
self.num_heads = num_heads
self.attention = d2l.DotProductAttention(dropout)
self.W_q = nn.LazyLinear(num_hiddens, bias=bias)
self.W_k = nn.LazyLinear(num_hiddens, bias=bias)
self.W_v = nn.LazyLinear(num_hiddens, bias=bias)
self.W_o = nn.LazyLinear(num_hiddens, bias=bias)
def forward(self, queries, keys, values, valid_lens):
# Shape of queries, keys, or values:
# (batch_size, no. of queries or key-value pairs, num_hiddens)
# Shape of valid_lens: (batch_size,) or (batch_size, no. of queries)
# After transposing, shape of output queries, keys, or values:
# (batch_size * num_heads, no. of queries or key-value pairs,
# num_hiddens / num_heads)
queries = self.transpose_qkv(self.W_q(queries))
keys = self.transpose_qkv(self.W_k(keys))
values = self.transpose_qkv(self.W_v(values))
if valid_lens is not None:
# On axis 0, copy the first item (scalar or vector) for num_heads
# times, then copy the next item, and so on
valid_lens = torch.repeat_interleave(
valid_lens, repeats=self.num_heads, dim=0)
# Shape of output: (batch_size * num_heads, no. of queries,
# num_hiddens / num_heads)
output = self.attention(queries, keys, values, valid_lens)
# Shape of output_concat: (batch_size, no. of queries, num_hiddens)
output_concat = self.transpose_output(output)
return self.W_o(output_concat)
为了允许多个头部的并行计算,上述 MultiHeadAttention 类使用下面定义的两个换位方法:
@d2l.add_to_class(MultiHeadAttention) #@save
def transpose_qkv(self, X):
"""Transposition for parallel computation of multiple attention heads."""
# Shape of input X: (batch_size, no. of queries or key-value pairs,
# num_hiddens). Shape of output X: (batch_size, no. of queries or
# key-value pairs, num_heads, num_hiddens / num_heads)
X = X.reshape(X.shape[0], X.shape[1], self.num_heads, -1)
# Shape of output X: (batch_size, num_heads, no. of queries or key-value
# pairs, num_hiddens / num_heads)
X = X.permute(0, 2, 1, 3)
# Shape of output: (batch_size * num_heads, no. of queries or key-value
# pairs, num_hiddens / num_heads)
return X.reshape(-1, X.shape[2], X.shape[3])
@d2l.add_to_class(MultiHeadAttention) #@save
def transpose_output(self, X):
"""Reverse the operation of transpose_qkv."""
X = X.reshape(-1, self.num_heads, X.shape[1], X.shape[2])
X = X.permute(0, 2, 1, 3)
return X.reshape(X.shape[0], X.shape[1], -1)
示例测试我们实现的 MultiHeadAttention 类:
num_hiddens, num_heads = 100, 5
attention = MultiHeadAttention(num_hiddens, num_heads, 0.5)
batch_size, num_queries, num_kvpairs = 2, 4, 6
valid_lens = torch.tensor([3, 2])
X = torch.ones((batch_size, num_queries, num_hiddens))
Y = torch.ones((batch_size, num_kvpairs, num_hiddens))
d2l.check_shape(attention(X, Y, Y, valid_lens),
(batch_size, num_queries, num_hiddens))
11.5.3. Summary¶
多头注意力通过查询,键和值的不同表示子空间结合了相同注意力集合的知识。要平行计算多头注意的多个头部,需要进行适当的张量操作。
Multi-head Attention机制通过并行计算多个头来从不同的表示子空间中学习注意力,捕捉输入的多种特征和依赖关系,尤其在长序列的情况下具有重要作用。
通过适当的张量操作(tensor manipulation),可以高效地计算多个头,避免计算成本和参数量的过度增长。
11.6. Self-Attention and Positional Encoding¶
自注意力机制是Transformer模型的核心,广泛应用于自然语言处理等领域,而位置编码用于补偿自注意力机制无法捕捉序列中位置信息的不足。
11.6.1. Self-Attention¶
自注意力机制的关键是每个输入序列中的token都可以根据其查询(query)与其他所有token的键(key)进行计算,从而决定如何更新该token的表示。
具体来说,每个token的查询会与其他所有token的键进行匹配,得出兼容性分数,然后基于这些分数,按权重求和所有token的值(value),以生成最终的token表示。
- 自注意力机制的计算过程:
给定输入序列
输出是一个与输入长度相同的序列
11.6.2. Comparing CNNs, RNNs, and Self-Attention¶
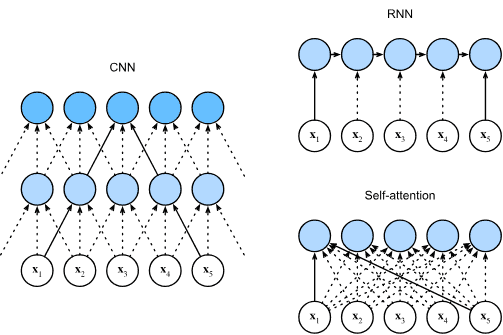
Fig. 11.6.1 Comparing CNN (padding tokens are omitted), RNN, and self-attention architectures.¶
自注意力的计算复杂度为
- CNN
CNN主要用于处理局部特征,通过卷积操作捕捉局部上下文信息。
其计算复杂度为
其中 k 是卷积核的大小。
CNN具有较短的路径长度,但计算过程中存在层级结构,因此最大路径长度为
- RNN
RNN按顺序处理每个token
其计算复杂度为
RNN的最大路径长度为
由于其顺序依赖性,无法并行化计算。
- Self-Attention
相比于CNN和RNN,自注意力能够并行计算,并且每个token都能直接与其他token建立连接(即路径长度为
但是,计算复杂度是
备注
All in all, both CNNs and self-attention enjoy parallel computation and self-attention has the shortest maximum path length. However, the quadratic computational complexity with respect to the sequence length makes self-attention prohibitively slow for very long sequences.
11.6.3. Positional Encoding¶
自注意力机制不包含顺序信息,因此无法直接捕捉序列中token的相对位置。为了弥补这一点,引入了位置编码,它为每个token添加了额外的位置信息,使得模型可以感知序列的顺序。
11.6.3.1. Absolute Positional Information¶
一种基于正弦和余弦函数的固定位置编码的简单方案
class PositionalEncoding(nn.Module): #@save
"""Positional encoding."""
def __init__(self, num_hiddens, dropout, max_len=1000):
super().__init__()
self.dropout = nn.Dropout(dropout)
# Create a long enough P
self.P = torch.zeros((1, max_len, num_hiddens))
X = torch.arange(max_len, dtype=torch.float32).reshape(
-1, 1) / torch.pow(10000, torch.arange(
0, num_hiddens, 2, dtype=torch.float32) / num_hiddens)
self.P[:, :, 0::2] = torch.sin(X)
self.P[:, :, 1::2] = torch.cos(X)
def forward(self, X):
X = X + self.P[:, :X.shape[1], :].to(X.device)
return self.dropout(X)
11.6.3.2. Relative Positional Information¶
除了绝对位置编码,位置编码也能捕捉相对位置关系。
通过对位置编码进行线性变换,可以表示任意两个token之间的相对位置偏移,从而使模型更容易学习到基于相对位置的注意力模式。
对于任何固定位置偏移
其中
对于任何固定偏移
11.6.4. Summary¶
自注意力机制使得每个token可以与其他所有token进行直接交互,从而捕捉长距离依赖。相比于CNN和RNN,自注意力计算可以并行化,最大路径长度最短,但由于计算复杂度是二次的,长序列处理的开销较大。
位置编码通过为每个token添加位置信息,使得自注意力机制能够处理顺序问题。位置编码可以是绝对的,也可以是相对的,帮助模型捕捉序列中的位置关系。
这两种机制结合起来,构成了Transformer的强大表达能力,使得它在许多自然语言处理任务中取得了显著的成功。
11.7. The Transformer Architecture¶
Transformer 就是 堆叠自注意力机制 + 残差连接 + 前馈网络,通过 Encoder 编码输入序列,再通过 Decoder 逐步自回归地生成输出序列,整套架构灵活且高度并行化,是现代大多数大型语言模型的基础。
11.7.1. Model¶
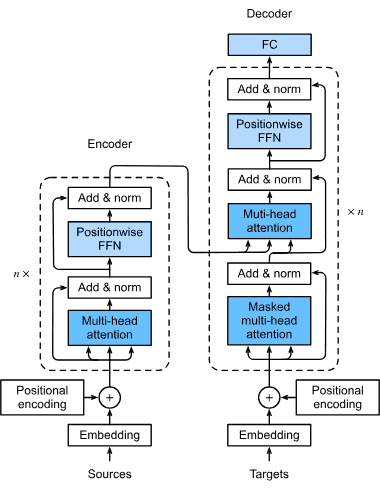
Fig. 11.7.1 The Transformer architecture.¶
- 整体结构
- Transformer 是一种 Encoder-Decoder 架构,整体分为两大块:
Encoder(编码器)
Decoder(解码器)
它是 序列到序列学习(seq2seq learning) 的一种改进方法,相比于之前流行的 Bahdanau Attention(注意力机制),Transformer 完全基于自注意力(self-attention) 机制来处理输入和输出序列。
- 输入处理
输入的 source sequence(输入序列) 和 target sequence(输出序列) 都要 先经过 embedding(词向量嵌入)
然后,位置编码(Positional Encoding) 被加到 embedding 上,告诉模型单词在序列中的位置,因为 Transformer 本身不具备序列顺序感知能力
之后,这些加了位置编码的向量会分别被送进 Encoder 和 Decoder
- Encoder 结构
- Encoder 是由 多个相同的层叠在一起,每一层包含 两个子层(sublayers):
- 多头自注意力层(Multi-Head Self-Attention)
自注意力机制,输入序列内部的各个词相互关注,捕捉上下文信息。
这里的 Query、Key、Value 都来自上一层 Encoder 的输出。
- 前馈神经网络(Feed-Forward Network)
逐位置应用的全连接网络,作用是增加模型的非线性表达能力。
- 残差连接(Residual Connection) 和 Layer Normalization
每个子层外面都有一个 残差连接(和 ResNet 类似),形式是:
保证输入和输出维度一致(
残差之后再做 LayerNorm,有助于训练稳定性。
Encoder 最终输出:每个位置一个 d 维向量,表示输入序列中每个词的表示。
- Decoder 结构
- Decoder 也由 多个相同层堆叠,但它比 Encoder 多了一个子层,总共 三个子层:
- Masked 多头自注意力层(Masked Multi-Head Self-Attention)
也是 Query、Key、Value 都来自 Decoder 的前一层输出。
但加了 mask,防止模型看到当前时间步之后的 token,保证自回归(autoregressive)性质。
Encoder-Decoder Attention - 这是 Decoder 特有的。 - Query 来自 Decoder,而 Key 和 Value 来自 Encoder 输出,实现输入输出序列之间的联系。
前馈神经网络
- 同样,每个子层也带有:
残差连接(输入 + 子层输出)
Layer Normalization
- 总结
- Transformer 整个设计理念:
完全基于 Attention,没有 RNN/CNN
位置编码补充序列顺序信息
残差连接 + LayerNorm 保证训练深层网络时的稳定性
Encoder 用于理解输入序列,Decoder 用于生成输出序列
Decoder 的 Masked Attention 保证 自回归生成(只看当前和之前的 token)
- 定义:残差连接(Residual Connection)
深度神经网络中常用的一种技巧,特别是在 ResNet(残差网络) 和 Transformer 里用得很多
核心思想:残差连接就是“跳过一层”直接把输入加到输出上。
公式:
- 直观理解: 模型学的不是直接输出,而是“输入和输出的差值”,即 residual(残差)
传统网络:
输入 x → 神经网络层 → 输出 y
残差连接:
输入 x → 神经网络层 → 得到 F(x) ↘ 加上输入 x 输出:y = F(x) + x
- 为什么要这样设计
- 解决深度网络训练困难
随着层数加深,容易出现 梯度消失或梯度爆炸,导致训练困难
残差连接可以让梯度 直接从后层传到前层,缓解这个问题
- 避免性能退化
实际上,如果网络没学到什么有用的东西,残差连接至少可以让网络学到“恒等映射”(即输出和输入一样)
这样网络至少不会比浅层网络表现更差,避免“加层反而效果下降”的问题
11.7.2. Positionwise Feed-Forward Networks¶
位置前馈网络(Positionwise Feed-Forward Network)
- 为什么称为”positionwise”(位置前馈)
- 关键点:
每个位置的向量是独立、逐个位置处理的!
同一个 FFN(同样的参数
- → 这就叫 positionwise —— 对每个“位置”单独应用相同的 FFN。
序列有很多 token,每个 token 有自己的表示(embedding 向量)。
所有 token 的向量都用同一个 FFN 进行处理,但每个 token 是单独处理,不考虑别的位置的信息。
- 输入和输出的形状:
输入X的形状是(batch size, number of time steps or sequence length in tokens, number of hidden units or feature dimension)。
输出Y的形状是(batch size, number of time steps, ffn_num_outputs)
结构:
class PositionWiseFFN(nn.Module): #@save
"""The positionwise feed-forward network."""
def __init__(self, ffn_num_hiddens, ffn_num_outputs):
super().__init__()
self.dense1 = nn.LazyLinear(ffn_num_hiddens)
self.relu = nn.ReLU()
self.dense2 = nn.LazyLinear(ffn_num_outputs)
def forward(self, X):
return self.dense2(self.relu(self.dense1(X)))
使用:
ffn = PositionWiseFFN(4, 8)
ffn.eval()
ffn(torch.ones((2, 3, 4)))[0]
# 输出
tensor([[ 0.6300, 0.7739, 0.0278, 0.2508, -0.0519, 0.4881, -0.4105, 0.5163],
[ 0.6300, 0.7739, 0.0278, 0.2508, -0.0519, 0.4881, -0.4105, 0.5163],
[ 0.6300, 0.7739, 0.0278, 0.2508, -0.0519, 0.4881, -0.4105, 0.5163]],
grad_fn=<SelectBackward0>)
11.7.3. Residual Connection and Layer Normalization¶
通过层规范化和批量规范化比较了不同维度上的规范化:
ln = nn.LayerNorm(2) bn = nn.LazyBatchNorm1d() X = torch.tensor([[1, 2], [2, 3]], dtype=torch.float32) # Compute mean and variance from X in the training mode print('layer norm:', ln(X), '\nbatch norm:', bn(X))
11.7.4. Encoder¶
11.7.5. Decoder¶
11.7.6. Training¶
11.7.7. Summary¶
11.8. Transformers for Vision¶
11.8.1. Model 11.8.2. Patch Embedding 11.8.3. Vision Transformer Encoder 11.8.4. Putting It All Together 11.8.5. Training 11.8.6. Summary and Discussion
11.9. Large-Scale Pretraining with Transformers¶
11.9.1. Encoder-Only 11.9.2. Encoder–Decoder 11.9.3. Decoder-Only 11.9.4. Scalability 11.9.5. Large Language Models 11.9.6. Summary and Discussion