Deep vanishing point detection: Geometric priors make dataset variations vanish¶

https://arxiv.org/abs/2203.08586
GitHub: https://github.com/yanconglin/VanishingPoint_HoughTransform_GaussianSphere
Google Scholar(28, 2025-04-21)
组织: Delft University of Technology, The Netherlands

概念¶

消失点（Vanishing Point）
- 在二维图像中，三维世界中一组平行线在透视投影(（Perspective Projection）)下交汇的点。
- 消失点就是你在照片里看到的「远方的汇聚点」，是平行线在透视下“看起来”会交汇的地方。
- 例子：站在铁路上看远方，两条铁轨本来是平行的，但在照片里，它们最终汇聚成一个点，这个点就是消失点。
- 对于常见的曼哈顿世界（建筑类图像），常常有三个主要消失点，分别对应 𝑥、𝑦、z 三个方向
- 消失点在图像中的应用：
  1. 三维结构恢复
    - 从 2D 图像反推出相机姿态或三维方向（如单图重建）
  2. 图像校正 / 拉直
    - 将倾斜的图像或透视畸变校正回正视图（如建筑图像矫正）
  3. 几何先验提取
    - 消失点可以揭示图像中的方向结构
    - 结合高斯球，可以用于方向聚类、曼哈顿方向识别
  4. 视觉SLAM / AR / 机器人定位
    - 用消失点辅助估计相机方向或场景结构
霍夫空间中的”bin” 是什么
- 霍夫变换会把图像中的点映射到参数空间（通常是极坐标的 θ-ρ 空间），为了计算机能处理，我们会把这个空间离散化，例如：
- θ 从 0° 到 180°，我们分成 180 个角度（每格 1°）
- ρ 从 -R 到 +R，我们分成 256 个距离格
- 这样整个 (θ, ρ) 参数空间就被分割成很多格子 ——每个格子就是一个 bin，它表示一条具体的直线！

Abstract¶

核心意思：作者提出了一种结合几何先验知识的新方法，用以改进图像中的消失点（Vanishing Point）检测，尤其是为了解决深度学习方法存在的几个关键问题。

Deep learning has improved vanishing point detection in images.
深度学习已经提升了图像中消失点检测的性能。

Yet, deep networks require expensive annotated datasets trained on costly hardware and do not generalize to even slightly different domains, and minor problem variants.
但是，深度网络存在一些缺点：需要昂贵的数据标注、依赖高成本的硬件，而且对稍有不同的领域或问题变种（比如稍微不同的消失点分布）泛化能力差。

Here, we address these issues by injecting deep vanishing point detection networks with prior knowledge.
本文通过向深度网络中注入先验知识（prior knowledge），来解决上述问题。

This prior knowledge no longer needs to be learned from data, saving valuable annotation efforts and compute, unlocking realistic few-sample scenarios, and reducing the impact of domain changes.
使用先验知识后，这部分信息不再需要从数据中学习，从而可以减少标注成本和训练计算量，使得少量样本学习成为可能，同时也能更好地应对领域变化。

Moreover, the interpretability of the priors allows to adapt deep networks to minor problem variations such as switching between Manhattan and non-Manhattan worlds.
更进一步，这些具有可解释性的几何先验也帮助模型应对问题设定的细微变化，比如从曼哈顿世界（建筑结构规整、消失点分布明确）切换到非曼哈顿世界（结构不规则、消失点更自由）的问题。

We seamlessly incorporate two geometric priors: (i) Hough Transform – mapping image pixels to straight lines, and (ii) Gaussian sphere – mapping lines to great circles whose intersections denote vanishing points.
作者引入了两种几何先验信息，自然地融合进了深度网络中：

(i) Hough变换：将图像中的像素映射到直线上；
(ii) 高斯球（Gaussian Sphere）：把图像中的直线映射到球面上的大圆，这些大圆的交点对应着消失点。

Experimentally, we ablate our choices and show comparable accuracy to existing models in the large-data setting.
通过实验，作者对各个设计进行了消融分析，并证明在大数据量场景中，他们的方法可以达到与现有方法相当的准确率。

We validate our model’s improved data efficiency, robustness to domain changes, adaptability to non-Manhattan settings.
并进一步验证了模型在数据效率（用更少数据训练）、对领域变化的鲁棒性、以及适应非曼哈顿结构的能力上有明显提升。

总结一句话：
- 这篇论文通过把几何先验（Hough变换+高斯球）引入深度网络，不仅提高了消失点检测的数据效率和泛化能力，还提升了模型在不同结构场景下的适应性和可解释性。

1. Introduction¶

引入了两个几何先验（geometric priors）来增强模型的泛化能力和数据效率。

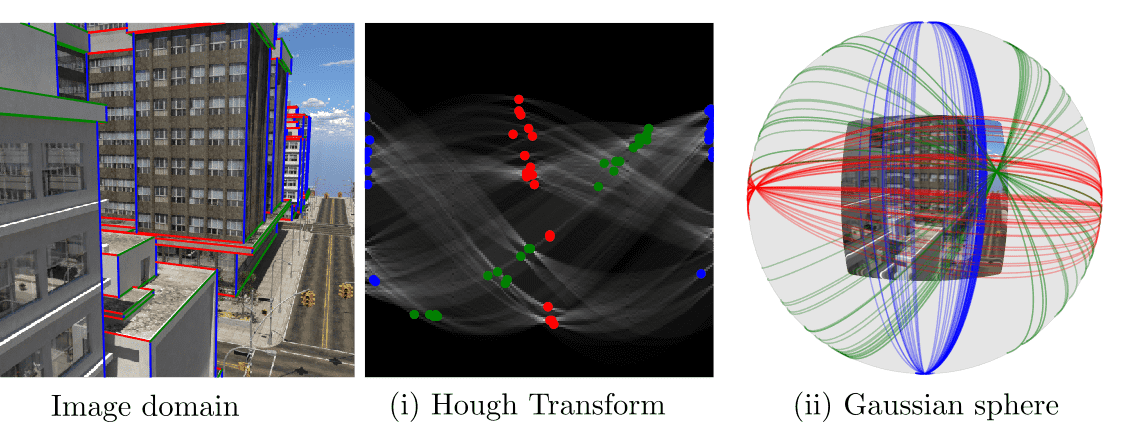
Figure 1:We add two geometric priors: (i) Hough Transform and (ii) Gaussian sphere mapping, for vanishing points detection. We transform learned image features to the Hough domain, where lines are mapped to individual bins. We further project the Hough bins to the Gaussian sphere, where lines become great circles and vanishing points are at the intersection of great circles. Each color represents a set of image lines related to a vanishing point. Adding geometric prior knowledge makes our model data-efficient, less dependent on domain-specifics, and easily adaptable to problem variations such as detecting a variable number of vanishing points.

作者在模型中加入了两种几何先验知识：

霍夫变换（Hough Transform）：用于将图像中的线段转换为参数空间中的“点(bin)”。
高斯球映射（Gaussian Sphere Mapping）：将这些 bin 映射到球面上，使线变成大圆（great circles），而消失点就是这些大圆的交点。

这张图可视化地展示了每组图像中的线如何映射成球面上的大圆，不同颜色表示归属于不同消失点的一组线。

研究背景与动机
- 消失点检测的重要性及其应用：
  - 应用场景：摄像机校准、场景理解、SLAM（同步定位与建图）、自动驾驶等。
  - 现有方法问题：
    - 深度学习方法虽然强大，但依赖大规模标注数据；
    - 标注过程昂贵，容易出错；
    - 培训资源消耗大；
    - 数据域变化（domain shift）时泛化能力差；
    - 问题稍变，网络就得重设计。

❗总结：现有深度学习方法太依赖数据，泛化差，调整成本高。

论文方法核心思路
- 通过引入几何先验来解决上述问题

Using geometric priors is data-efficient as this knowledge no longer needs to be learned from data.

核心优势：
- 不需要从头学习几何规则（比如“线的交点是消失点”），节省数据和计算；
- 更容易泛化到新场景；
- 更容易解释和适配任务变体。

方法细节-实现了以下两个可训练的模块：
1. 霍夫变换模块：将每条线表示成极坐标对的 (offset, angle)，变成 Hough 空间的 bin。
2. 高斯球映射模块：
  - 将 Hough 空间的 bin 映射到单位球面上；
  - 图像中的线 → 球面上的大圆；
  - 消失点 → 大圆的交点；
  - 好处是可以检测在图像视野外的消失点（例如透视中的点）。

两者都能端到端训练，并利用深度网络提取的特征进行优化。

贡献总结（Contributions）
1. 提出将 CNN 特征 → 霍夫空间 → 高斯球空间的方法，用于消失点检测；
2. 在 ScanNet 和 SceneCity Urban 数据集上达到与 SOTA 类似精度；
3. 添加先验后，在小数据集上表现更好（数据效率更高）；
4. 成功适配“消失点数不固定”的问题（NYU Depth 数据集上，消失点数量从 1 到 8）；
5. 在跨数据集测试中表现更稳健，减少了 domain shift 的影响。

总结一句话

这篇论文的核心理念是：通过引入霍夫变换和高斯球映射两种几何先验知识，把一些“理所当然的几何关系”注入模型中，从而减少对数据的依赖、增强泛化能力，并提高模型对任务变体的适应性。

2. Related Work¶

✅ 基于几何的消失点检测(Geometry-based vanishing point detection)¶

核心观点：
- 消失点本质是图像中直线的交点。
- 如何检测这些线：
  - 轮廓检测（contour detection）
  - 点-线双映射（point-to-line dual mapping）
  - 最常用的方式是 霍夫变换（Hough Transform）。
与本文关系：
- 本文正是将 霍夫变换当作几何先验引入模型，是对这一传统方法的现代深度学习扩展。
将线组合成消失点（Combining lines to vanishing points）
- 基于概率：计算线是否通过同一点；
- 投票机制：比如 RANSAC 或累加器；
- 假设检验：比如 J-Linkage 判断哪些线属于同一消失点；
- 线聚类（clustering）、EM算法、分支界定法（branch-and-bound） 等也可用于组合线。
- 局限点：
  
  这些方法虽然有效，但都没有引入真实 3D 世界中的先验知识（例如线→球面大圆→交点这样的几何逻辑）。
高斯球几何先验（Gaussian Sphere）
- 核心思想：
  - 图像中的线 = 高斯球上的大圆；
  - 大圆的交点 = 消失点；
  - 高斯球将“无界的图像平面”映射到“有界的球面”，更易建模。
- 优点：
  - 限制了搜索空间（正则化），对数据较少时的深度学习模型很有帮助；
  - 本文正是借助这个先验知识构建球面映射模块。

✅ 基于学习的消失点检测(Learning-based vanishing point detection)¶

关键思路：
- 使用深度学习模型（如 CNN）从大量标注数据中学习消失点；
- 常见流程包括：线检测 → 投影 → 网络训练 → 后处理；
- 一些工作还用了圆锥卷积（conic convolutions），更适合球面数据。
本文的不同之处：

本文不是追求更大的数据、更深的模型，而是关注小样本、跨域、非曼哈顿世界等更真实但困难的场景。

✅ 对抗领域偏移(Robustness to domain shifts)¶

问题：
- 传统方法靠几何先验，不依赖数据，所以天生跨域；
- 但这些方法没办法充分利用深度网络的表达能力；
- 反过来，深度模型对 domain shift（如跨数据集）非常敏感。
已有应对策略：
- 域自适应、通用化、多域训练等，但都需要复杂的架构变化。
本文策略：

提出一种方法，在不改变网络结构的前提下，结合几何知识与深度学习，提升对 domain shift 的鲁棒性。

✅ 曼哈顿 vs 非曼哈顿世界(Manhattan versus non-Manhattan world)¶

曼哈顿世界假设：
- 假设场景中有 3 个正交方向（所以有 3 个正交消失点）；
- 适合建筑场景，但很多真实情况（如斜坡、自由构架）不满足这个假设。
应对非曼哈顿世界的方法：
- 多模型拟合、地平线检测、球面上的非极大值抑制等。
本文的方法：

不强加曼哈顿假设，而是通过 Hough + Gaussian sphere + 聚类算法 来检测数量不固定的多个消失点。

🔚 总结¶

这部分工作回顾梳理了从几何方法、深度学习方法到对抗领域偏移和非曼哈顿情况的处理方式，凸显了本文的创新点在于：

利用几何先验（霍夫 + 球面）来约束模型；
不依赖大数据，鲁棒性强；
能自然适配不同的任务设定（如非曼哈顿、跨域）；
同时仍保留了深度学习的表达能力。

3. Geometric priors for VP detection¶

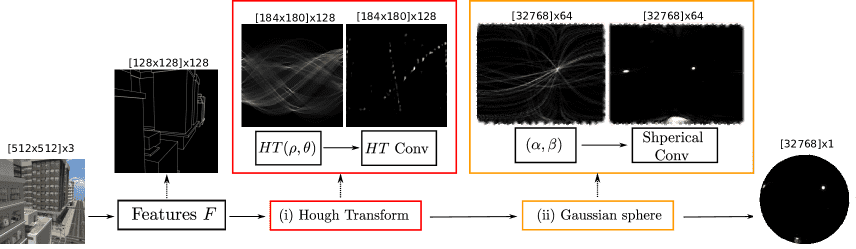
Figure 2:Overview: The model starts from in input image, and predicts vanishing points on the Gaussian hemisphere by relying on two geometric priors: (i) Hough Transform, and (ii) Gaussian sphere mapping. We use a convolutional network to learn features which are then mapped to Hough space, where each bin is a line. We filter the Hough space and project Hough bins to the Gaussian hemisphere and apply spherical convolutions to find vanishing points. We indicate the size of the learned features above, where the last dimension is the number of channels. We sample 32,768 points on the hemisphere using the Fibonacci lattice, resulting in features maps of size 32,768. Our model learns to classify spherical points as vanishing points or not using a binary cross-entropy loss. There is no intermediate supervision.

任务目标：
- 从一张图像中检测消失点。
- 消失点常用于理解图像的几何结构，尤其在结构化环境如城市街景中十分关键。
模型流程概览：
1. 输入图像 → 卷积网络提取特征。
2. 特征 → 投影到霍夫空间（Hough space），每个 bin 对应一条直线。
3. 过滤噪声 → 投影这些线条到高斯球面（Gaussian sphere）。
4. 在球面上进行卷积（EdgeConv） → 精确定位消失点。

🧩 (i) 霍夫变换（Hough Transform）¶

目的：
- 将图像中的像素特征转换为一组参数化直线。
核心公式：
- 图像中的一组像素点沿一条直线，投票给某个 (ρ, θ) 组合（即一条线）：
- $H T (ρ, θ) = \sum_{i} F (ρ \cos θ - i \sin θ, ρ \sin θ + i \cos θ)$
- 这意味着，我们对每一条可能的直线组合 (ρ, θ)，根据图像特征图 F 做加权投票。
参数设置：
- 图像特征图尺寸：128×128
- Hough 空间分辨率：184 个 ρ（距离），180 个 θ（角度）
去噪处理：
- 使用 1D 卷积 沿 ρ 轴平滑响应，保留局部最大值（对应于“潜在线条”）。

🧭 (ii.1) 高斯球面映射（Gaussian Sphere Mapping）¶

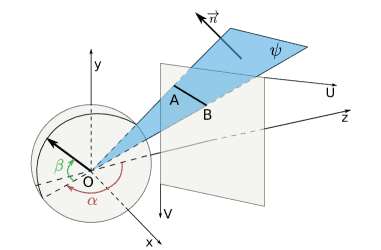
Figure 3: Gaussian sphere representations for vanishing points: (a) The Gaussian sphere is a unit sphere located at the camera center, $O$ . Points on the sphere are encoded by two angles: $(α, β)$ the azimuth and the elevation, respectively. A line segment $AB$ in the image plane together with the camera center $O$ forms a plane $ψ$ , highlighted in blue. To define the mapping from the image to the sphere, we only need to know the normal $\vec{n}$ to the plane $ψ$ . (b) Image lines are projected as great circles on the sphere. The intersection of multiple great circles on the sphere represents a vanishing point.

目标：
- 将霍夫空间中的直线（ρ, θ）映射到球面上的大圆弧（great circles），寻找交点作为候选消失点。
关键几何：
- 设相机中心为 O
- 图像中一条线段 AB，连同 O 构成一个平面 ψ
- 这个平面的法向量 $\vec{n} = \frac{\vec{O A} \times \vec{O B}}{‖ \vec{O A} \times \vec{O B} ‖}$
- 投影这条线段对应的大圆弧到高斯球（单位球）
球面坐标：
- 方位角（azimuth）α：从 z 轴在 xz 平面旋转的角度
- 仰角（elevation）β：从 xz 平面向 y 轴的角度
- 利用公式：$ $β (α, \vec{n}) = \tan^{- 1} (\frac{- n_{x} \sin α - n_{z} \cos α}{n_{y}})$ $
- 每条线都可以映射到球面上的一条大圆。多个大圆的交点就是潜在的消失点。
采样方式：
- 使用 Fibonacci lattice（斐波那契点阵）均匀采样高斯半球，共 32,768 个点
- 将所有 Hough 空间的线条映射到这些点上，最近邻匹配
- 映射关系预计算后存为形状 [N_ρ × N_θ × M] 的张量（其中 M 是 α 的采样数量，如 1024）

🧠 (ii.2) 球面卷积（Spherical Convolution）¶

目的：
- 在球面上定位精确的消失点。
方法：
- 将球面采样点视为点云，构建 KNN 图
- 使用 EdgeConv（边卷积）对每个点的局部邻域做聚合
- 共用 5 层 EdgeConv，每层使用：
  - 全连接层
  - BatchNorm
  - LeakyReLU
- 使用特征连接（concatenation）增强信息流
- 最后使用二分类（是否是消失点）进行训练

📌 总结一句话：
- 这套模型创新性地将消失点检测转换为先映射线到球面、再在球面上做分类的任务，核心优势是引入几何先验结构（线→大圆→交点），极大地提升了泛化能力与鲁棒性。

4. Experiments¶

作者设计的几何先验（HT变换 + 球面卷积）确实提升了性能，尤其是在小数据量和精度要求高的任务中。
在Manhattan世界假设下，我们的方法几乎能匹敌或超过现有SOTA，参数少，运行快。
在非Manhattan的NYU Depth数据集上也具备较好适应性，显示出模型较强的泛化能力。

4.1 Exp 1: Evaluating model choices¶

他们的模型在数据效率和稳定性方面表现优越。

4.2 Exp 2: Validation on large datasets¶

模型选择实验展示了他们设计中：
- 结合传统几何方法（如 Hough）与深度学习能显著提升表现；
- 球面卷积、精细量化和端到端训练都是关键；
数据效率实验说明他们的方法：
- 能在数据稀缺下保持稳定、优异表现；
- 比其他依赖手工特征的模型鲁棒性更强；
泛化与大数据验证：
- 在大规模训练下也不掉精度；
- 在小规模无微调时依然领先，说明具备良好的泛化能力；
- 并且具有较高的推理速度。

4.3 Exp 3: Challenging scenarios¶

作者模型通过引入几何先验（Geometric Priors），在以下挑战场景中都显著优于现有方法：
- 训练数据极少时
- 场景不符合曼哈顿假设（如真实世界复杂环境）
- 训练测试数据集分布不一致时（跨域泛化）

5. Conclusion and limitations¶

论文的贡献在于：
- 引入了霍夫变换和高斯球映射这两个几何先验，
- 在多样化、复杂的数据场景下表现优异，尤其能突破“曼哈顿世界”的限制。
但仍存在两大问题：
1. 预计算映射带来的量化误差限制了精度；
2. 需要大量标注数据，难以直接用于数据不足或弱监督的场景。