深度学习相关¶
computation graph(计算图)¶
一种用图形结构表示计算过程的方法,尤其在深度学习中,它用于表示模型的计算步骤和操作依赖关系
计算图(computation graph)的
节点表示操作(例如加法、乘法)或变量(例如输入、权重)
边表示数据流动或依赖关系
通过计算图,我们可以直观地追踪每一步计算过程,这在自动微分和反向传播中尤为重要
作用和特点
表示计算流程:计算图展示了从输入到输出的整个计算过程,将复杂的模型计算拆分成一系列简单操作。
依赖关系的直观表示:在图中,从输入到输出的路径展示了变量和操作之间的依赖关系。
例如,在深度神经网络中,图中每一层的输出是下一层的输入。
用于自动微分和反向传播:计算图让反向传播更高效。
在反向传播时,从输出层反向遍历计算图,应用链式法则逐步计算梯度,从而更新模型参数。
示例:
对于一个简单的神经网络,其中 z = x * w + b 是输出
计算图会表示 x 和 w 的乘法操作、b 的加法操作,并最终得出 z 的计算结果
Gradients Descent 梯度下降¶
概念:
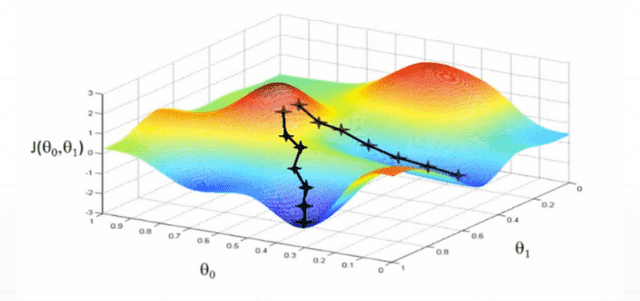
构建Loss(预测值与实际值之间的偏差)与相关权值变量θ(0)和θ(1)的函数关系J(θ(0), θ(1)),在函数图像上随机取初值点,然后求初值点的导数(也就是梯度),并沿着导数最倾斜的方向按照一定的步长更新J点,以及类推总能找到J(min)的局部最优解,也就是预测值与实际值偏差最小的状态。¶
激活函数¶
概念:在多层神经网络中,上层节点的输出和下层节点的输入之间具有一个函数关系,这个函数称为激活函数(激励函数)。
作用:不使用激活函数的话,神经网络的每层都只是做线性变换,多层输入叠加后也还是线性变换。因为线性模型的表达能力通常不够,所以这时候就体现了激活函数的作用了,激活函数可以引入非线性因素。
常用激活函数:有sigmoid、ReLu等。
Loss Function 损失函数¶
概念:也称为误差函数,是输出层的输出O与目标值t之间的偏差函数。这个偏差值有多种表示方式,如均方误差MSE、CEL等。





