权重衰减(L2正则化)¶
L2正则化（也称为权重衰减）是一种在机器学习模型训练中用于防止过拟合的技术。它通过在损失函数中添加一个与模型权重平方和成正比的惩罚项，限制模型参数的大小，从而提高模型的泛化能力。
数学定义¶
对于给定的损失函数 \(L(\mathbf{w}, b)\) ，L2正则化通过添加权重向量 \(\mathbf{w}\) 的平方和惩罚项来形成新的目标函数：
新的损失函数
\[L_{reg}(\mathbf{w}, b) = L(\mathbf{w}, b) + \frac{\lambda}{2} \|\mathbf{w}\|^2\]
标准 SGD 公式
\[w = w - \eta \cdot \nabla L(w)\]
加入权重衰减后的更新公式
\[\begin{split}w = w - \eta \cdot (\nabla L(w) + \lambda w) \\
= (1 - \eta \lambda)w - \eta \nabla L(w)\end{split}\]
L2正则化回归的小批量随机梯度下降更新
\[\begin{aligned}
\mathbf{w} & \leftarrow \left(1- \eta\lambda \right) \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \mathbf{x}^{(i)} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)
\end{aligned}\]
目标¶
控制模型复杂度：通过在损失函数中引入权重向量范数（ \(|\mathbf{w}|^2\) ）作为惩罚项，限制模型参数的大小，降低模型复杂度。
正则化目标函数： 原始目标：最小化训练集上的预测误差。 新目标：最小化训练误差与正则化项之和，即：
\[\begin{split}L(\mathbf{w}, b) + \frac{\lambda}{2} \|\mathbf{w}\|^2 \\
\lambda 是超参数，决定正则化的强度 \\
\lambda > 0 会约束权重向量\end{split}\]
作用¶
防止过拟合： 通过对大权重值施加更大的惩罚，L2正则化促使模型偏好于较小且分散的权重，从而降低模型对训练数据的过度拟合，提高对新数据的泛化能力。
权重衰减： 在每次参数更新时，L2正则化会使权重值逐渐减小，避免权重值过大导致模型复杂度增加。
由于 L2 正则化会促使权重趋近于 0，因此总体复杂性可能会降低。
L2 正则化绝不会将权重完全推向零，即从模型中移除一些特征。
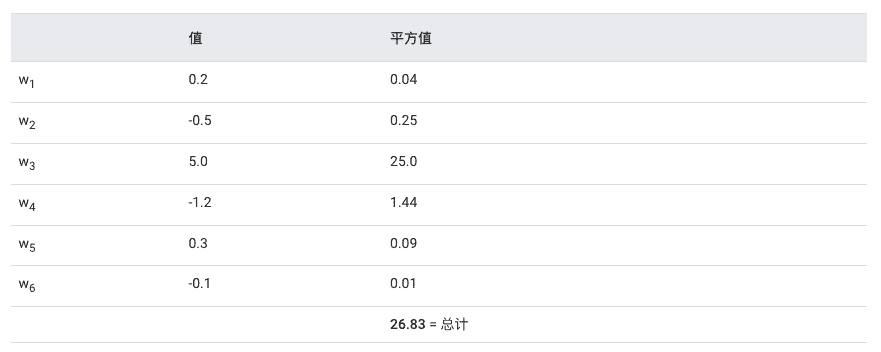
具有 6 个权重的模型计算 L2 正则化项的过程：接近零的权重对 L2 正则化影响不大，但较大的权重可能会产生巨大影响（单个权重 (w3) 约占总复杂度的 93%。）。L2 正则化会使权重趋近 0，但绝不会使权重完全为零。¶