损失函数-回归-均方误差(MSE)¶

Mean Squared Error
公式:

\[\begin{split}\begin{array}{l} L = \frac{1}{N} \sum_{i=1}^N{(y_i - \hat{y}_i)^2} \\ 说明: \\ \hat(y): 模型预测值，通常称为预测输出 \end{array}\end{split}\]

优点：对大误差更敏感，有助于减少显著偏差。
缺点：对异常值过于敏感，可能导致模型不鲁棒。

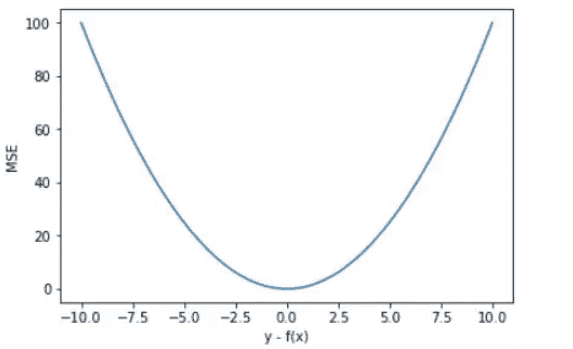
https://img.zhaoweiguo.com/uPic/2024/11/uxZltj.png — MSE 曲线的特点是光滑连续、可导，便于使用梯度下降算法，是比较常用的一种损失函数。而且，MSE 随着误差的减小，梯度也在减小，这有利于函数的收敛，即使固定学习因子，函数也能较快取得最小值。¶

平方误差有个特性，就是当 yi 与 f(xi) 的差值大于 1 时，会增大其误差；当 yi 与 f(xi) 的差值小于 1 时，会减小其误差。这是由平方的特性决定的。也就是说， MSE 会对误差较大（>1）的情况给予更大的惩罚，对误差较小（<1）的情况给予更小的惩罚。从训练的角度来看，模型会更加偏向于惩罚较大的点，赋予其更大的权重。

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(1, 20, 40)
y = x + [np.random.choice(4) for _ in range(40)]
y[-5:] -= 8
X = np.vstack((np.ones_like(x),x))    # 引入常数项 1
m = X.shape[1]
# 参数初始化
W = np.zeros((1,2))

# 迭代训练
num_iter = 20
lr = 0.01
J = []
for i in range(num_iter):
   y_pred = W.dot(X)
   loss = 1/(2*m) * np.sum((y-y_pred)**2)
   J.append(loss)
   W = W + lr * 1/m * (y-y_pred).dot(X.T)

# 作图
y1 = W[0,0] + W[0,1]*1
y2 = W[0,0] + W[0,1]*20
plt.scatter(x, y)
plt.plot([1,20],[y1,y2])
plt.show()