损失函数-回归-Huber 损失¶
平滑平均绝对误差
公式:
\[\begin{split}\begin{array}{l}
L_{\delta}(\alpha) = \left\{\begin{matrix}
\frac{1}{2}\alpha^2， & for |\alpha| \le \delta ,\\
\delta \cdot (|\alpha| - \frac{1}{2}\delta ) & for |\alpha| > \delta
\end{matrix}\right. \\
\end{array}\end{split}\]
参数 a 通常表示 residuals，写作 y−f(x)，当 a = y−f(x) 时，Huber loss 定义为
\[\begin{split}\begin{array}{l}
L_{\delta}(y, f(x)) = \left\{\begin{matrix}
\frac{1}{2}(y-f(x))^2， & for |y-f(x)| \le \delta ,\\
\delta \cdot (|y-f(x)| - \frac{1}{2}\delta ) & for |y-f(x)| > \delta
\end{matrix}\right. \\
\end{array}\end{split}\]
说明:
δ 是 HuberLoss 的参数，\\
y是真实值， \\
f(x)是模型的预测值
备注
这儿用 f(x) 而不用 \(\hat{y}\) 主要是为了表明这是从模型的函数形式出发推导的。 f(x) ：表示模型的函数表达式，是从输入特征 𝑥 到输出预测值的映射。 \(\hat{y}\) 表示具体的预测值，是模型 𝑓(𝑥) 在给定输入 𝑥 后的输出。
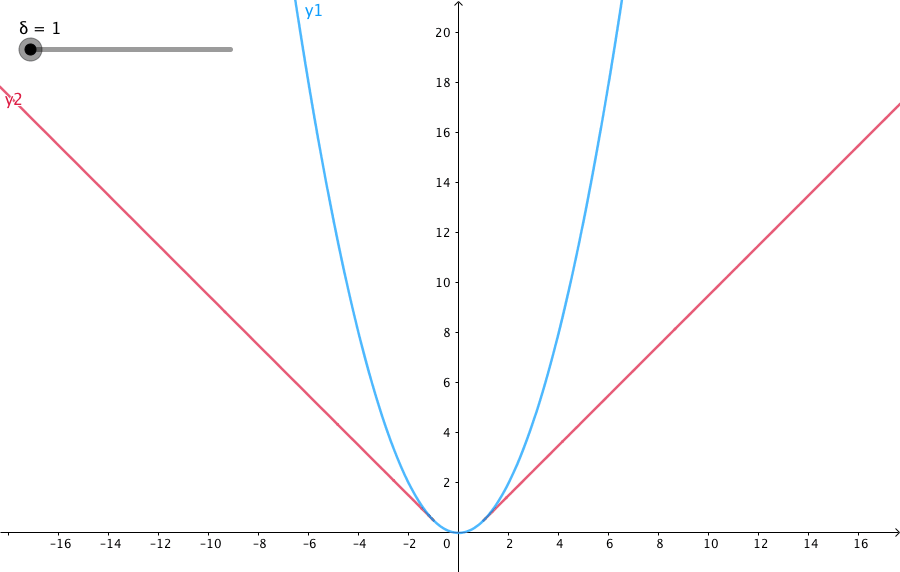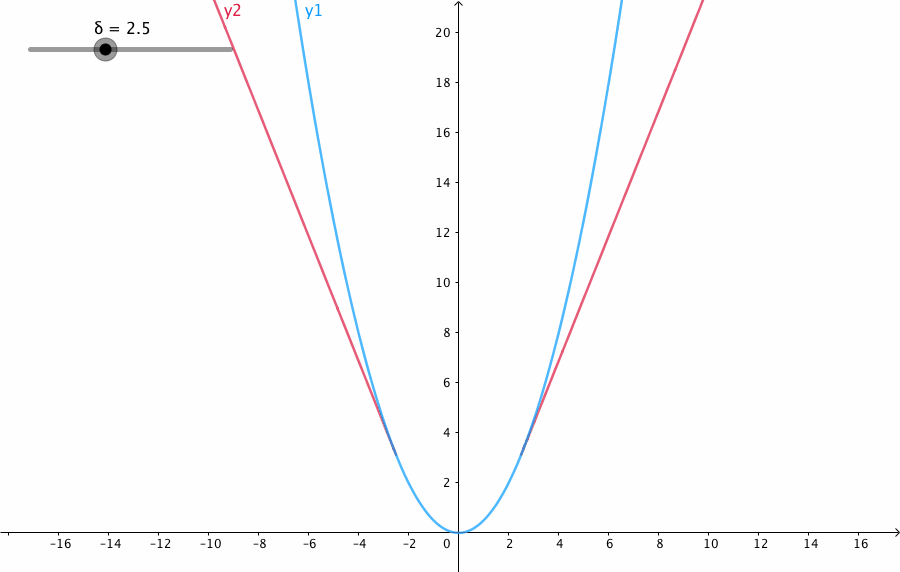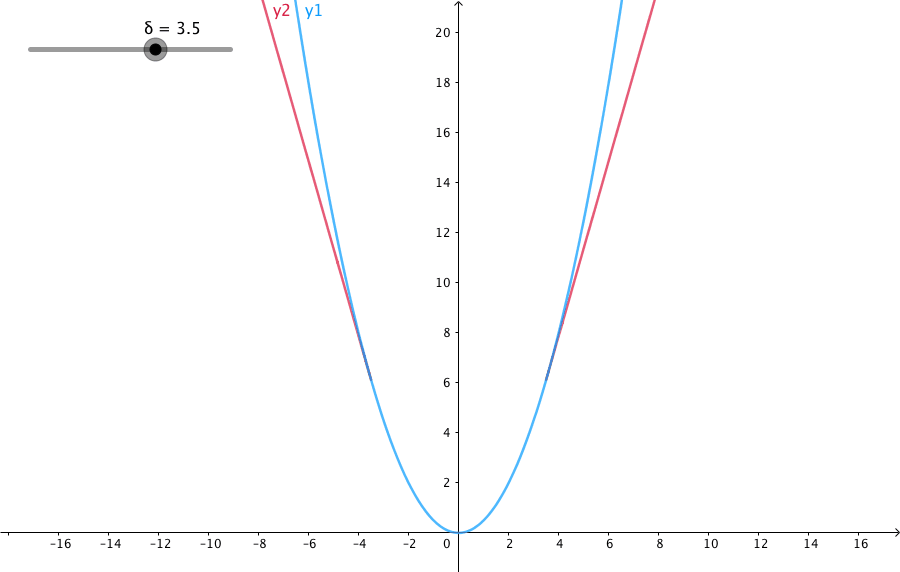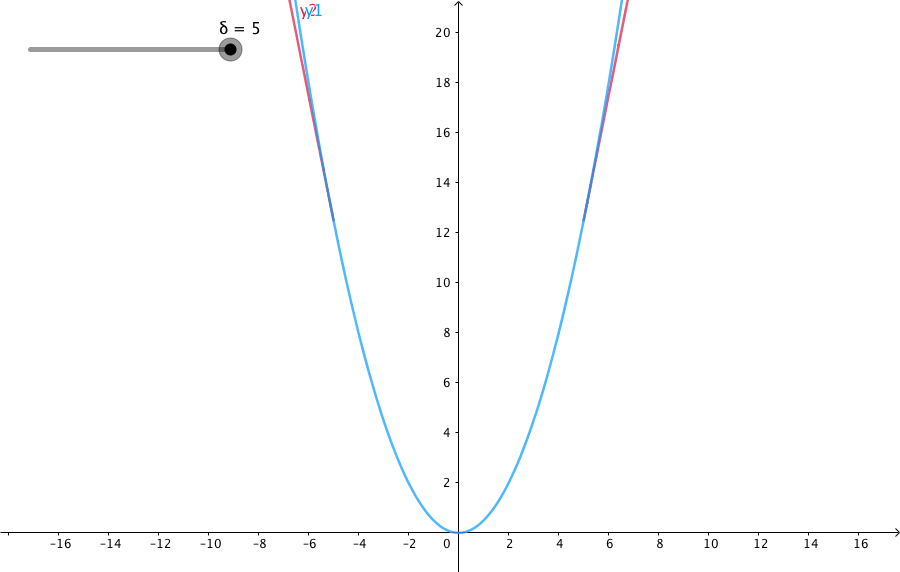
当预测偏差小于 δ 时，它采用平方误差,
当预测偏差大于 δ 时，采用的线性误差。
优点：结合了 MSE 和 MAE 的优点，对异常值更鲁棒。
应用场景：适用于数据中存在少量异常值的回归任务。
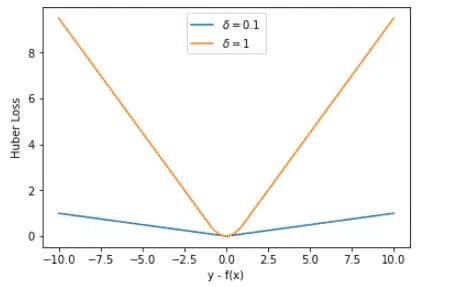
Huber Loss 在 |y−f(x)| > δ 时，梯度一直近似为 δ，能够保证模型以一个较快的速度更新参数。当 |y−f(x)| ≤ δ 时，梯度逐渐减小，能够保证模型更精确地得到全局最优值。因此，Huber Loss 同时具备了前两种损失函数的优点。¶
x = np.linspace(1, 20, 40)
X = np.vstack((np.ones_like(x),x)) # 引入常数项 1
m = X.shape[1]
# 参数初始化
W = np.zeros((1,2))
# 迭代训练
num_iter = 20
lr = 0.01
delta = 2
J = []
for i in range(num_iter):
y_pred = W.dot(X)
loss = 1/m * np.sum(np.abs(y-y_pred))
J.append(loss)
mask = (y-y_pred).copy()
mask[y-y_pred > delta] = delta
mask[mask < -delta] = -delta
W = W + lr * 1/m * mask.dot(X.T)
# 作图
y1 = W[0,0] + W[0,1]*1
y2 = W[0,0] + W[0,1]*20
plt.scatter(x, y)
plt.plot([1,20],[y1,y2],'r--')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Huber')
plt.show()
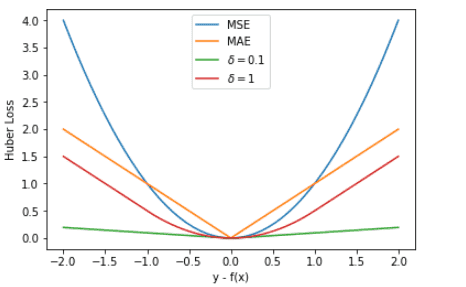
MSE、MAE、Huber Loss: MSE 的 Loss 下降得最快，MAE 的 Loss 下降得最慢，Huber Loss 下降速度介于 MSE 和 MAE 之间。¶