分布-正态分布(Normal Distribution)¶
正态分布（Normal Distribution），又称高斯分布，是一种重要的连续概率分布，广泛应用于自然科学和社会科学领域。正态分布是描述随机变量的一种理想化模型，它的概率密度函数呈钟形，具有对称性和特定的数学特性。
\[f(x)=\frac{1}{\sqrt{2 \pi \sigma^2}} e^{-\frac{(x-\mu)^2}{2 \sigma^2}}\]
其中:
μ：均值（mean），表示分布的中心。
𝜎^2 ：方差（variance），表示分布的宽度，反映数据的离散程度
𝜎 越大，分布越宽、越平
𝜎 越小，分布越窄、越尖
当随机变量 𝑋 服从正态分布时，记作:
𝑋 ∼ 𝑁(𝜇, 𝜎^2)
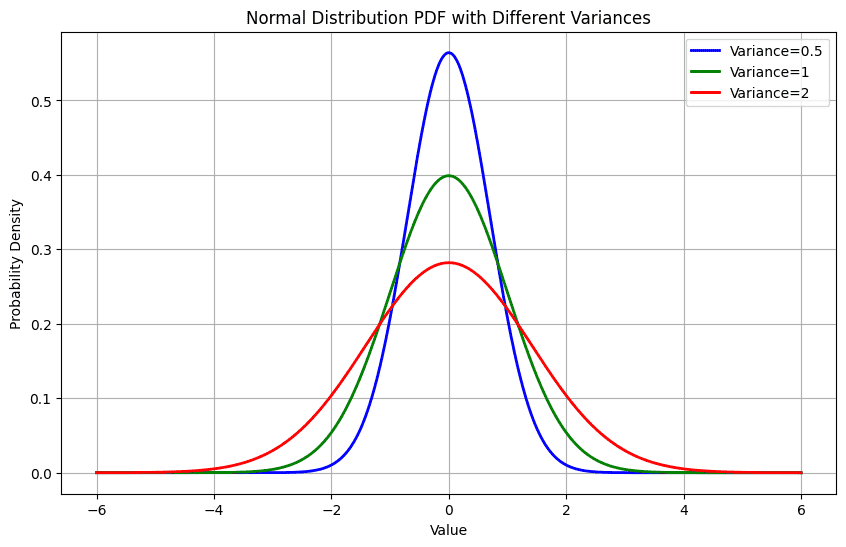
特点¶
对称性:
正态分布以均值 𝜇 为中心，关于 𝜇 对称。
均值、中位数和众数相等，且都等于 𝜇。
钟形曲线:
曲线呈钟形，峰值位于均值 𝜇，两侧逐渐向零无限接近，但永远不会达到零。
68-95-99.7 规则（经验法则）:
在正态分布中：
数据有约 68% 位于 𝜇±𝜎 范围内。
数据有约 95% 位于 𝜇±2𝜎 范围内。
数据有约 99.7% 位于 𝜇±3𝜎 范围内。
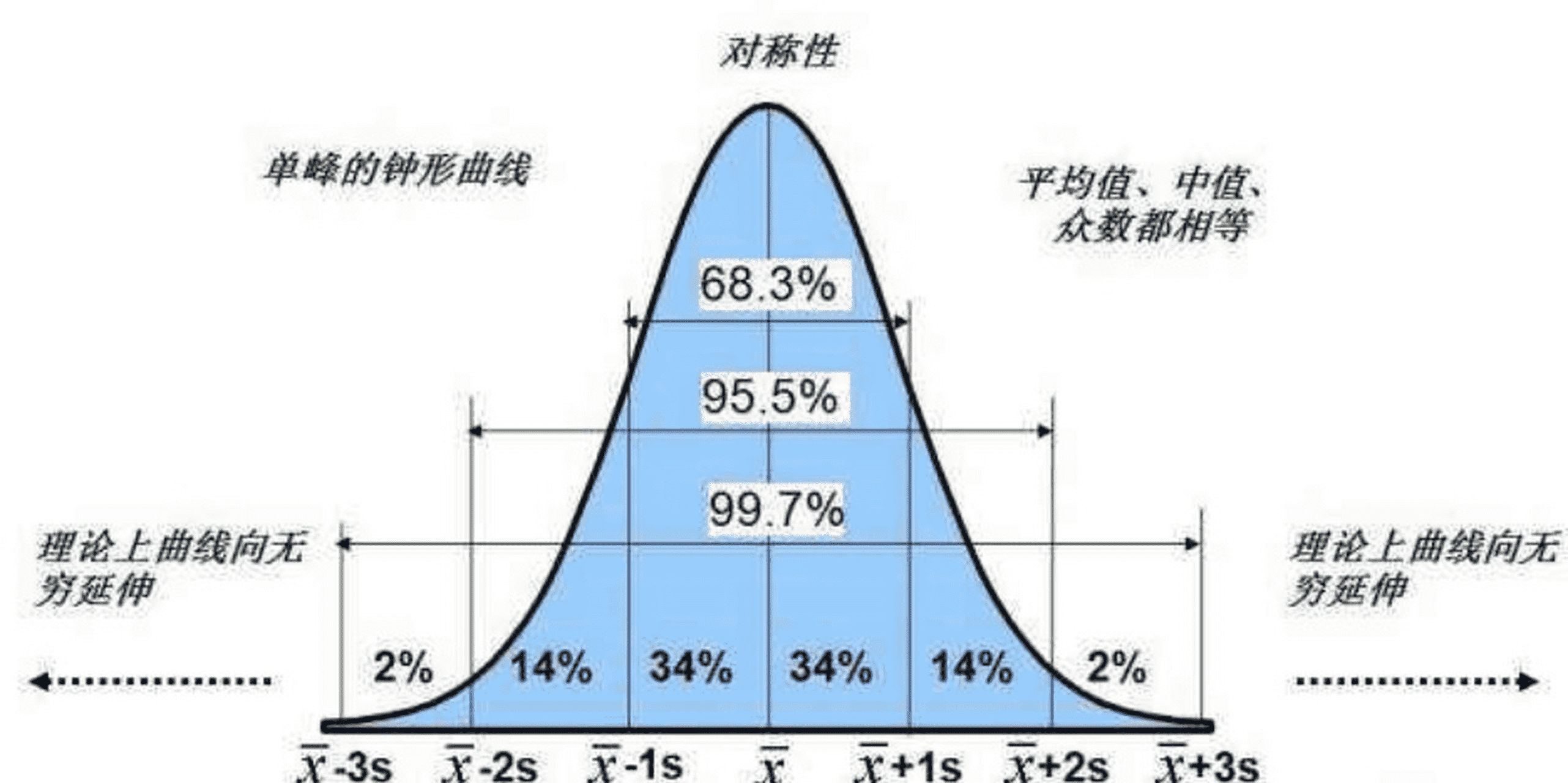
标准化:
标准正态分布是特殊的正态分布，其均值为 0，标准差为 1，即 𝑁(0,1)。
可通过标准化公式将任意正态分布转化为标准正态分布：
𝑍=(𝑋−𝜇)/𝜎
其中 𝑍 是标准化后的变量。
应用¶
自然现象:
人类身高、体重、智商等通常服从正态分布。
测量误差或噪声往往近似服从正态分布。
统计分析:
大量统计方法基于正态分布假设，例如线性回归、假设检验。
金融领域:
用于建模资产回报、风险估计。
机器学习与数据科学:
特征工程中对数据标准化。
假设数据满足正态分布，简化模型假设。
标准正态分布¶
标准正态分布是特定参数下的高斯分布:
𝜇=0, 𝜎2=1
其概率密度函数为:
\[𝑓(𝑥)=\frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}}\]
标准正态分布的累积分布函数 Φ(𝑥) 常用于统计表或数值计算。
多维高斯分布¶
多维高斯分布是高斯分布的扩展，适用于多变量的情况。
其概率密度函数为：
\[ \begin{align}\begin{aligned}f(\mathbf{x})=\frac{1}{(2 \pi)^{n / 2}|\boldsymbol{\Sigma}|^{1 / 2}} \exp \left(-\frac{1}{2}(\mathbf{x}-\mu)^{\top} \boldsymbol{\Sigma}^{-1}(\mathbf{x}-\mu)\right)\\\begin{split}
其中: \\
- \mathbf{x} \in \mathbb{R}^{n} 是随机变量向量 \\
- \mu \in \mathbb{R}^{n} 是均值向量 \\
- \boldsymbol{\Sigma} \in \mathbb{R}^{n \times n} 是协方差矩阵，描述变量之间的相关性\end{split}\end{aligned}\end{align} \]