概率密度函数(Probability Density Function, PDF)¶

概率密度函数（PDF）是连续随机变量的一种重要概念，用于描述随机变量取值在某一区间内的可能性。
概率密度函数不能直接表示单个点的概率，而是通过积分计算出随机变量在某个范围内的概率。

定义¶

若随机变量 𝑋 是连续的，则其概率密度函数 $𝑓_{𝑋} (𝑥)$ 满足以下条件：

\begin{array}{r} \begin{array}{l} 1. f_{X} (x) \geq 0, 对 所 有 x \\ 2. 随 机 变 量 X 在 某 区 间 [a, b] 内 的 概 率 为 : \\ P (a \leq X \leq b) = \int_{a}^{b} f_{X} (x) d x \\ 3. 概 率 密 度 函 数 在 整 个 定 义 域 上 的 积 分 为 1 : \\ \int_{- \infty}^{\infty} f_{X} (x) d x = 1 \end{array} \end{array}

直观理解¶

$f_{X} (x)$ 表示随机变量在某一点的”密度”, 不是概率。
$f_{X} (x)$ 越大, 随机变量在该点附近取值的可能性越高。
真正的概率需要通过积分计算，例如：
- $P (a \leq X \leq b)$ 是 $f_{X} (x)$ 在区间 [a, b] 的积分。

概率密度函数的特性¶

非负性：

f_{X} (x) \geq 0, \forall x

归一性：

\int_{- \infty}^{\infty} f_{X} (x) d x = 1

区间概率：随机变量在区间 [a, b] 内取值的概率为：

P (a \leq X \leq b) = \int_{a}^{b} f_{X} (x) d x

概率与微分的关系:
- $P (X = c) = 0$ 对任何具体值 c 都成 $\overset{↓}{}$ ，因为积分的区间长度为零。

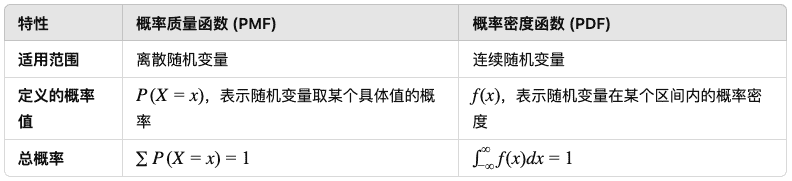
https://img.zhaoweiguo.com/uPic/2024/12/v0xpsC.png — 与概率质量函数的区别¶

常见概率密度函数¶

均匀分布

\begin{array}{r} \begin{matrix} \begin{matrix} f_{X} (x) = {\begin{cases} \frac{1}{b - a}, & if a \leq x \leq b \\ 0, & otherwise \end{cases} \end{matrix} \\ 随 机 变 量 在 区 间 [a, b] 上 均 匀 分 布, 所 有 值 的 密 度 相 等 。 \end{matrix} \end{array}

正态分布

\begin{array}{r} \begin{matrix} f_{X} (x) = \frac{1}{\sqrt{2 π} σ} e^{- \frac{(x - μ)^{2}}{2 σ^{2}}} \\ \begin{matrix} μ 是 均 值, σ 是 标 准 差 \\ 正 态 分 布 的 图 形 为 对 称 的 钟 形 曲 线 \end{matrix} \end{matrix} \end{array}

指数分布

\begin{array}{r} \begin{matrix} \begin{matrix} f_{X} (x) = {\begin{cases} λ e^{- λ x}, & x \geq 0 \\ 0, & x < 0 \end{cases} \end{matrix} \\ 用 于 描 述 事 件 发 生 的 时 间 间 隔 。 \end{matrix} \end{array}

伽马分布

\begin{array}{r} \begin{matrix} f_{X} (x) = \frac{λ^{k} x^{k - 1} e^{- λ x}}{Γ (k)}, x \geq 0 \\ Γ (k) 是 伽 马 函 数 。 \end{matrix} \end{array}

统计量计算¶

期望值

E [X] = \int_{- \infty}^{\infty} x f_{X} (x) d x

方差

\begin{array}{r} \begin{matrix} Var (X) = E [X^{2}] - (E [X])^{2} \\ \begin{matrix} 其 中 : \\ E [X^{2}] = \int_{- \infty}^{\infty} x^{2} f_{X} (x) d x \end{matrix} \end{matrix} \end{array}