主页

索引

模块索引

搜索页面

基本-导数

基本运算

常数法则

• 如果 f(x)=c （其中 c 是一个常数），那么 f′(x)=0

幂法则-Power Rule

如果 $f(x)=x^n$ 那么 $f\prime (x)=n{x}^{n-1}$

和差法则-Sum and Difference Rule

$$\begin{array}{r}\begin{array}{c}\begin{array}{c}\mathrm{如}\mathrm{果}:f(x)=g(x)+h(x)\\ \mathrm{那}\mathrm{么}:f\prime (x)=g\prime (x)+h\prime (x)\end{array}\\ \mathrm{如}\mathrm{果}:f(x)=g(x)-h(x)\mathrm{那}\mathrm{么}:f\prime (x)=g\prime (x)-h\prime (x)\end{array}\end{array}$$

乘积法则-Product Rule

$$\begin{array}{r}\mathrm{如}\mathrm{果}:f(x)=g(x)h(x)\\ \mathrm{那}\mathrm{么}:f\prime (x)=g\prime (x)h(x)+g(x)h\prime (x)\end{array}$$

商法则-Quotient Rule

$$\begin{array}{r}\mathrm{如}\mathrm{果}:f(x)=\frac{g(x)}{h(x)}\\ \mathrm{那}\mathrm{么}:f\prime (x)=\frac{g\prime (x)h(x)-g(x)h\prime (x)}{(h(x){)}^2}\end{array}$$

指数函数的导数

$$\begin{array}{r}\begin{array}{c}\begin{array}{c}\mathrm{如}\mathrm{果}:f(x)=e^x\\ \mathrm{那}\mathrm{么}:f\prime (x)=e^x\end{array}\\ \begin{array}{c}\mathrm{对}\mathrm{于}\mathrm{一}\mathrm{般}\mathrm{的}\mathrm{指}\mathrm{数}\mathrm{函}\mathrm{数}(a>0)\\ \mathrm{如}\mathrm{果}:f(x)=a^x\mathrm{那}\mathrm{么}:f\prime (x)=a^{x}ln(a)\end{array}\end{array}\end{array}$$

对数函数的导数

$$\begin{array}{r}\begin{array}{c}\begin{array}{c}\mathrm{如}\mathrm{果}:f(x)=ln(x)\\ \mathrm{那}\mathrm{么}:f\prime (x)=\frac{1}{x}\end{array}\\ \begin{array}{c}\mathrm{对}\mathrm{于}\mathrm{一}\mathrm{般}\mathrm{的}\mathrm{对}\mathrm{数}\mathrm{函}\mathrm{数}(a>0)\\ \mathrm{如}\mathrm{果}:f(x)=lo{g}_a(x)\\ \mathrm{那}\mathrm{么}:f\prime (x)=\frac{1}{xln(a)}\end{array}\end{array}\end{array}$$

三角函数的导数

$$\begin{array}{r}\mathrm{如}\mathrm{果}:f(x)=sin(x),\mathrm{那}\mathrm{么}f\prime (x)=cos(x)\\ \mathrm{如}\mathrm{果}:f(x)=cos(x),\mathrm{那}\mathrm{么}f\prime (x)=-sin(x)\end{array}$$

chain rule: 链式法则

复合函数的导数将是构成复合这有限个函数在相应点的导数的乘积，就像锁链一样一环套一环，故称链式法则

若h(x)=f(g(x))，则h'(x)=f'(g(x))g'(x)

链式法则是微积分中的求导法则，用以求一个复合函数的导数。
所谓的复合函数，是指以一个函数作为另一个函数的自变量。
如f(x)=3x，g(x)=x+3，g(f(x))就是一个复合函数，并且g(f(x))=3x+3

$$\frac{\partial u}{\partial x}=\frac{\partial u}{\partial v}\cdot \frac{\partial v}{\partial x}$$

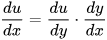
多元链式法则

• 定义：如果函数 u=φ(t) 和 v=ψ(t)都在点 t 可导，函数z=f(u,v)在对应点(u,v)具有连续偏导数（重点），那么复合函数z=f[φ(t),ψ(t)]在点t可导，且有：

$$\frac{\partial z}{\partial t}=\frac{\partial z}{\partial u}\cdot \frac{\partial u}{\partial t}+\frac{\partial z}{\partial v}\cdot \frac{\partial v}{\partial t}$$

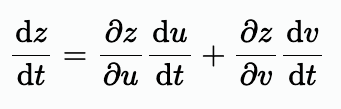
证明

设t获得增量Δt，此时u=φ(t),v=ψ(t)的对应增量为Δu,Δv，由此，z=f(u,v)获得增量Δz。因为函数z=f(u,v)在点(u,v)有连续偏导数，于是全增量Δz可表示为（全微分的充分条件）

$$\mathrm{\Delta }z=\frac{\partial z}{\partial u}\mathrm{\Delta }u+\frac{\partial z}{\partial v}\mathrm{\Delta }v+{\epsilon }_1\mathrm{\Delta }u+{\epsilon }_2\mathrm{\Delta }v$$

• 上式两边各除以Δt

$$\frac{\mathrm{\Delta }z}{\mathrm{\Delta }t}=\frac{\partial z}{\partial u}\frac{\mathrm{\Delta }u}{\mathrm{\Delta }t}+\frac{\partial z}{\partial v}\frac{\mathrm{\Delta }v}{\mathrm{\Delta }t}+{\epsilon }_1\frac{\mathrm{\Delta }u}{\mathrm{\Delta }t}+{\epsilon }_2\frac{\mathrm{\Delta }v}{\mathrm{\Delta }t}$$

• 取极限Δt→0

$$\frac{\partial z}{\partial t}=\frac{\partial z}{\partial u}\cdot \frac{\partial u}{\partial t}+\frac{\partial z}{\partial v}\cdot \frac{\partial v}{\partial t}$$

备注

神经网络中的多元函数大多是仿射函数（激活函数不是，但是也符合可微条件），符合上述全微分的充分条件，所以可以使用反向传播来计算所有参数的梯度。

• 仿射函数（Affine Function）是指一种线性变换加上一个常数项的函数，形式为： 𝑓(𝑥)=𝑊𝑥+𝑏f(x)=Wx+b 其中：𝑊 是权重矩阵，𝑥 是输入向量，𝑏 是偏置（或称为截距）项。

• 在神经网络的每一层中，输入通常会先经过一个仿射变换（即：加权求和，再加上偏置），然后再通过激活函数。激活函数一般是非线性的，比如 ReLU 或 Sigmoid

参考

• 多元复合函数的求导法则（多元链式法则）: https://www.cnblogs.com/qizhou/p/13033929.html

主页

索引

模块索引

搜索页面