前向/反向传播¶
“正向传播”求损失,“反向传播”回传误差
神经网络每层的每个神经元都可以根据误差信号修正每层的权重
神经元¶
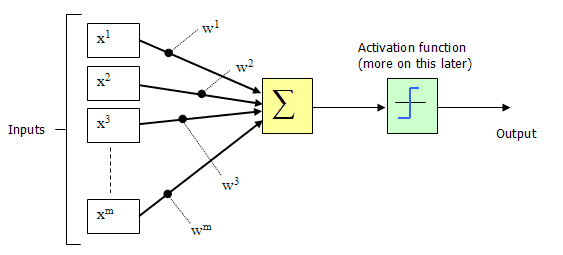
M-P(麦卡洛克-皮茨, McCulloch-Pitts)神经元模型,它是感知机的基础模型。M-P神经元是一种二元分类模型,将加权求和的结果输入到激活函数中,判断输出是0或1。神经元的输出: θ 为我们之前提到的神经元的激活阈值,函数 f(⋅) 也被称为是激活函数。¶
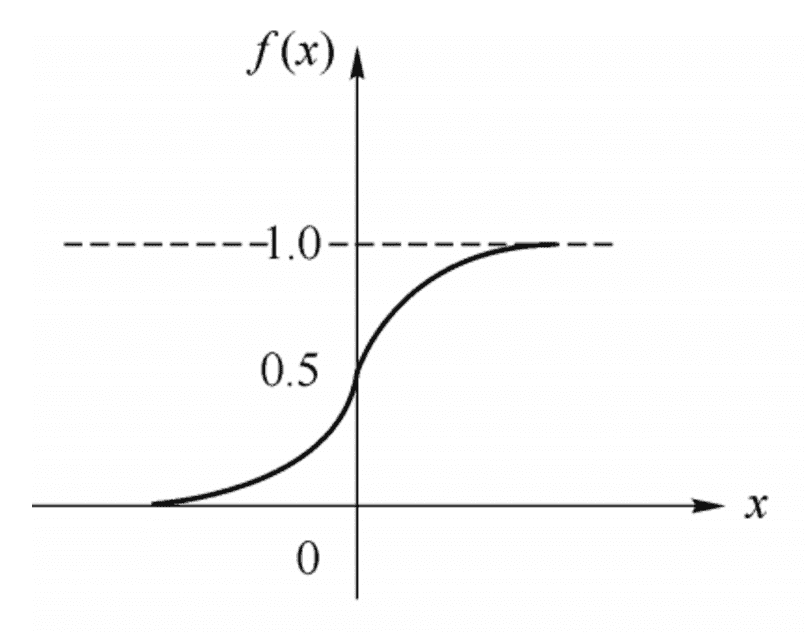
常用的方法是用sigmod函数来表示激活函数,表达式为
感知机和神经网络¶
感知机(Perceptron)通常被认为是最早的一种人工神经网络模型之一,它由Frank Rosenblatt于1958年提出。尽管感知机的概念相对简单,但它为后续更复杂的神经网络的发展奠定了基础。
感知机(perceptron)是由两层神经元(输入层和输出层)组成的结构,输入层用于接受外界输入信号,输出层(也被称为是感知机的功能层)就是M-P神经元,将这些数据通过权重进行处理后,输出一个结果。输出层通过对输入信号加权求和并应用一个激活函数来决定输出值。
备注
从结构上来说,一个标准的感知机模型实际上只包含一层“权重”节点,这些节点接收输入数据,并通过加权求和的方式计算出一个值,然后通过激活函数(通常是阶跃函数)来决定输出。因此,从严格意义上讲,感知机可以被看作是只有单层的神经网络,而不是两层。但是,当人们提到感知机有“两层神经元”的时候,他们可能是指包括输入层在内的整个结构。在这种描述中:输入层:不被视为真正的神经元层,因为这里的节点只是将输入数据传递给下一层,没有进行任何计算或变换。输出层:这一层包含了执行实际计算的神经元,每个神经元接收来自输入层的数据,对其进行加权求和,并通过激活函数产生最终输出。 这种表述方式有助于与多层神经网络(如深度学习中的模型)进行对比和理解。 ——fromGPT
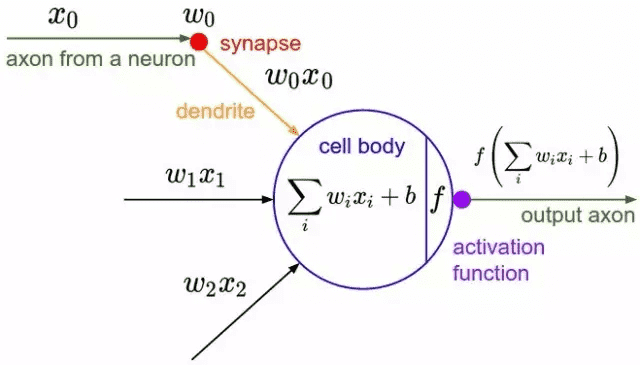
一个输入层具有三个神经元(分别表示为x0、x1、x2)的感知机结构。(神经元的主要组成部分包括轴突(axon)、树突(dendrite)、胞体(soma)和突触(synapse))¶
感知机模型的公式表示:
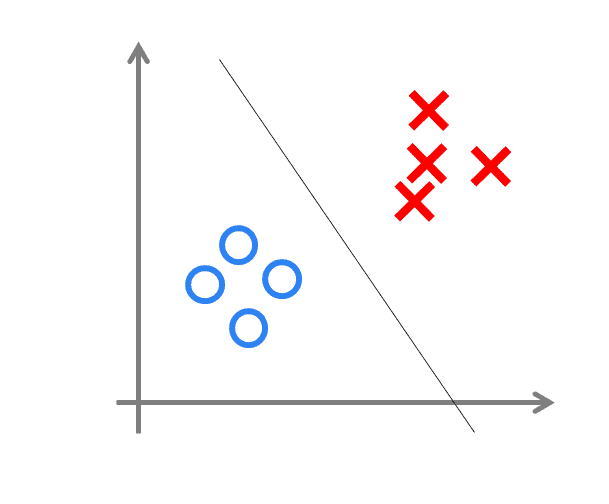
线性可分问题的示意图¶
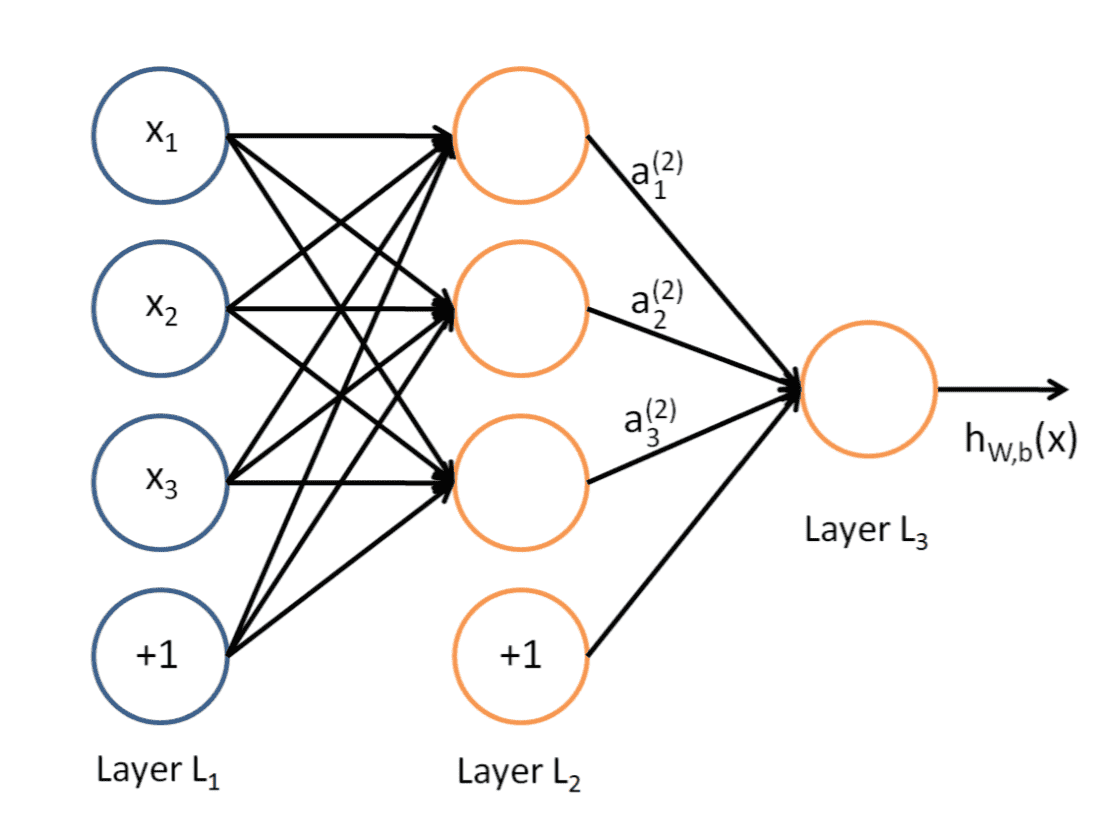
典型的三层神经网络的基本构成,Layer L1是输入层,Layer L2是隐含层,Layer L3是输出层¶
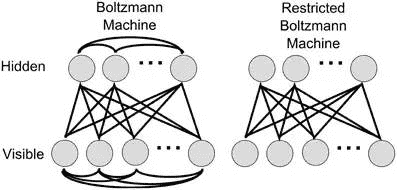
Boltzmann机和受限Boltzmann机¶
神经网络中有一类模型是为网络状态定义一个“能量”,能量最小化时网络达到理想状态,而网络的训练就是在最小化这个能量函数。Boltzmann(玻尔兹曼)机就是基于能量的模型,其神经元分为两层:显层和隐层。显层用于表示数据的输入和输出,隐层则被理解为数据的内在表达。Boltzmann机的神经元都是布尔型的,即只能取0、1值。标准的Boltzmann机是全连接的,也就是说各层内的神经元都是相互连接的,因此计算复杂度很高,而且难以用来解决实际问题。因此,我们经常使用一种特殊的Boltzmann机——受限玻尔兹曼机(Restricted Boltzmann Mechine,简称RBM),它层内无连接,层间有连接,可以看做是一个二部图。
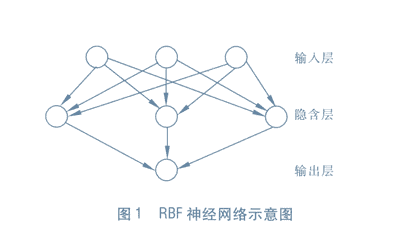
RBF网络¶
RBF(Radial Basis Function)径向基函数网络是一种单隐层前馈神经网络,它使用径向基函数作为隐层神经元激活函数,而输出层则是对隐层神经元输出的线性组合。
训练RBF网络通常采用两步:
1> 确定神经元中心,常用的方式包括随机采样,聚类等;
2> 确定神经网络参数,常用算法为BP算法。
ART网络¶
ART(Adaptive Resonance Theory)自适应谐振理论网络是竞争型学习的重要代表,该网络由比较层、识别层、识别层阈值和重置模块构成。ART比较好的缓解了竞争型学习中的“可塑性-稳定性窘境”(stability-plasticity dilemma),可塑性是指神经网络要有学习新知识的能力,而稳定性则指的是神经网络在学习新知识时要保持对旧知识的记忆。这就使得ART网络具有一个很重要的优点:可进行增量学习或在线学习。
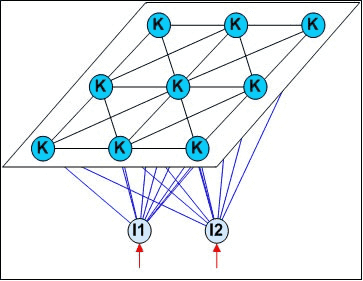
SOM网络¶
SOM(Self-Organizing Map,自组织映射)网络是一种竞争学习型的无监督神经网络,它能将高维输入数据映射到低维空间(通常为二维),同时保持输入数据在高维空间的拓扑结构,即将高维空间中相似的样本点映射到网络输出层中的临近神经元。
forward propagation 前向传播¶
FP算法
前向传播(forward propagation或forward pass) 指的是:按顺序(从输入层到输出层)计算和存储神经网络中每层的结果。
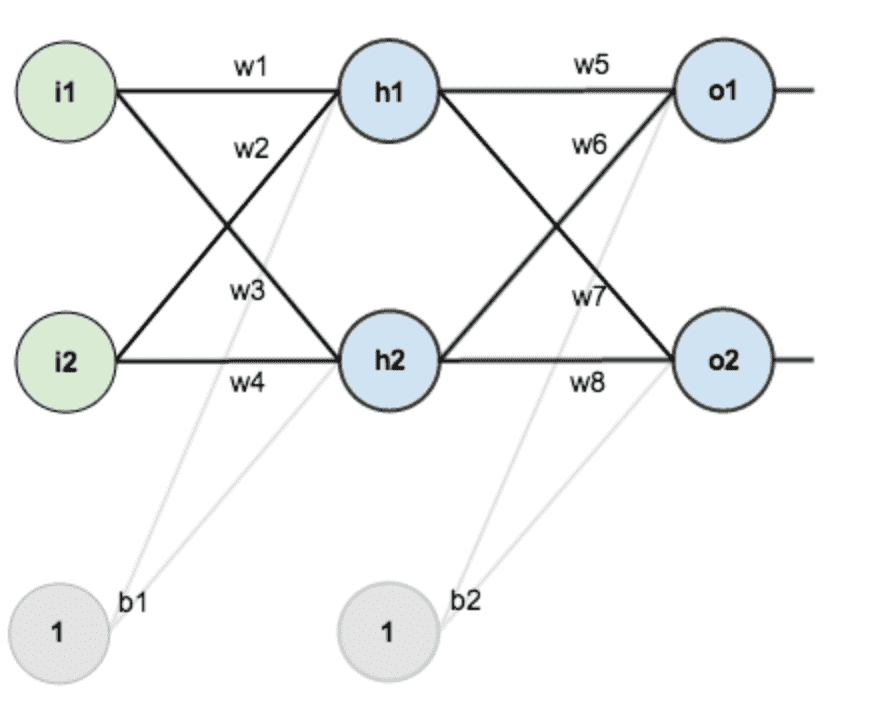
第一层是输入层,包含两个神经元i1,i2,和偏置项(bias term)b1;第二层是隐含层,包含两个神经元h1,h2和偏置项(bias term)b2,第三层是输出o1,o2,每条线上标的wi是层与层之间连接的权重,激活函数我们默认为sigmoid函数。¶
赋上初值:
输入数据 i1=0.05, i2=0.10
输出数据 o1=0.01, o2=0.99
初始权重 w1=0.15, w2=0.20, w3=0.25, w4=0.30
w5=0.40, w6=0.45, w7=0.50, w8=0.55
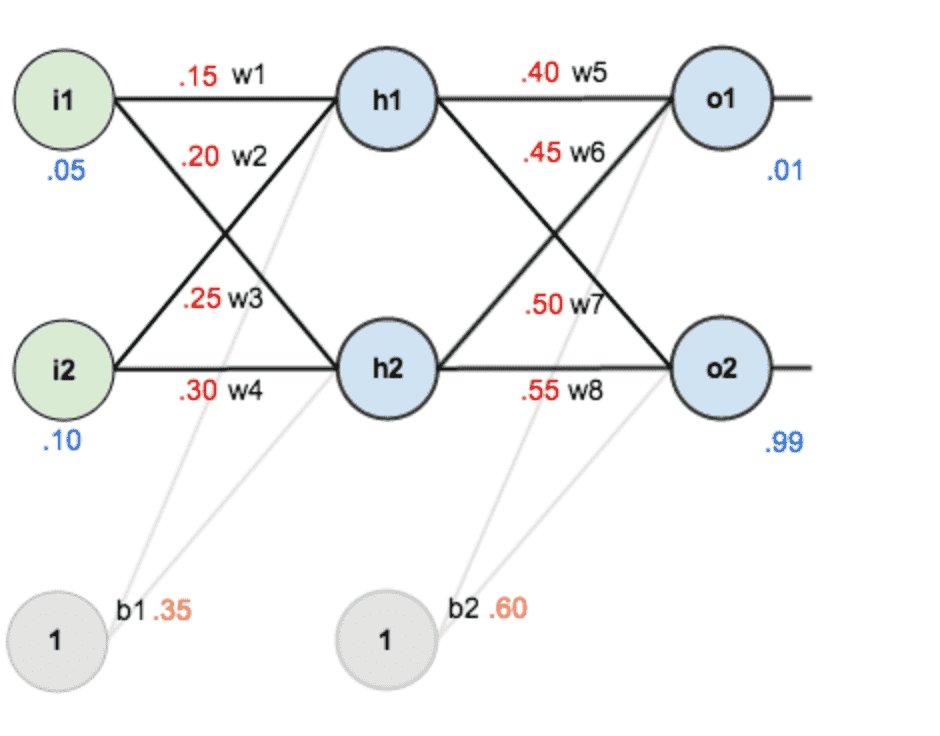
1.输入层—->隐含层¶
计算神经元h1的输入加权和:
神经元h1的输出o1:(此处用到激活函数为sigmoid函数):
同理,可计算出神经元h2的输出o2:
2.隐含层—->输出层¶
计算输出层神经元o1和o2的值
备注
前向传播的过程就结束了,我们得到输出值为[0.75136079 , 0.772928465],与实际值[0.01 , 0.99]相差还很远
backward propagation 反向传播¶
BP算法,也叫 δ算法
反向传播(backward propagation或backpropagation)指的是计算神经网络参数梯度的方法。 简言之,该方法根据微积分中的链式规则,按相反的顺序从输出层到输入层遍历网络。 该算法存储了计算某些参数梯度时所需的任何中间变量(偏导数)。
反向传播:“误差反向传播”的简称,是一种与最优化方法(如梯度下降法)结合使用的,用来训练人工神经网络的常见方法。 该方法对网络中所有权重计算损失函数的梯度。 这个梯度会反馈给最优化方法,用来更新权值以最小化损失函数。
1.计算总误差¶
误差:(square error):
有两个输出,所以分别计算o1和o2的误差,总误差为两者之和
2.隐含层—->输出层(w5-w8)的权值更新¶
以权重参数w5为例,如果我们想知道w5对整体误差产生了多少影响,可以用整体误差对w5求偏导求出(链式法则)
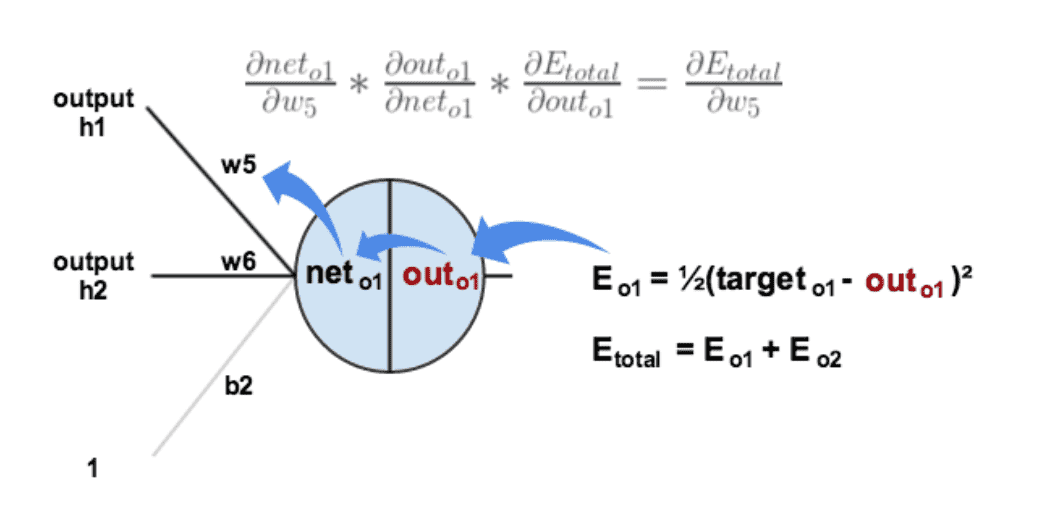
误差是怎样反向传播的¶
计算
计算
计算
最后三者相乘(计算出整体误差E(total)对w5的偏导值):
上面3个公式合并:
为了表达方便,用
因此,整体误差E(total)对w5的偏导公式可以写成:
更新w5的值(这儿
同理,可更新w6,w7,w8:
3.输入层—>隐含层的权值(w1-w4)更新¶
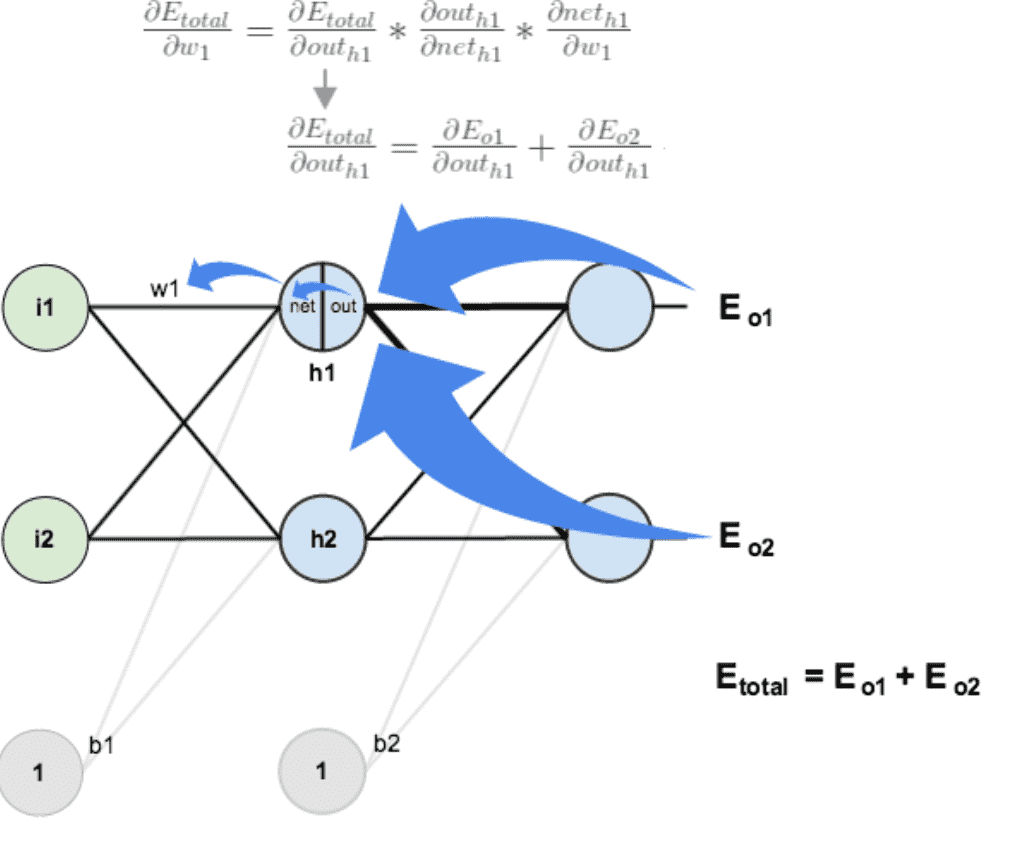
与上面说的差不多,但是有个地方需要变一下,在上文计算总误差对w5的偏导时,是从out(o1)—>net(o1)—>w5,但是在隐含层之间的权值更新时,是out(h1)—>net(h1)—>w1,而out(h1)会接受E(o1)和E(o2)两个地方传来的误差,所以这个地方两个都要计算。¶
计算
先计算
再计算
再计算
三者相乘
上面的过程汇总
最后,更新w1的权值:(这儿
同理,可更新w1,w2,w3:
备注
这样误差反向传播法就完成了,最后我们再把更新的权值重新计算,不停地迭代,在这个例子中第一次迭代之后,总误差E(total)由0.298371109下降至0.291027924。迭代10000次后,总误差为0.000035085,输出为[0.015912196,0.984065734](原输入为[0.01,0.99]),证明效果还是不错的。
1、重写为
2、求导:
3、计算内部的导数:
4、代入第2步:
5、由于
演示Demo¶
#coding:utf-8
import random
import math
#
# 参数解释:
# "pd_" :偏导的前缀
# "d_" :导数的前缀
# "w_ho" :隐含层到输出层的权重系数索引
# "w_ih" :输入层到隐含层的权重系数的索引
class NeuralNetwork:
LEARNING_RATE = 0.5
def __init__(self, num_inputs, num_hidden, num_outputs, hidden_layer_weights = None, hidden_layer_bias = None, output_layer_weights = None, output_layer_bias = None):
self.num_inputs = num_inputs
self.hidden_layer = NeuronLayer(num_hidden, hidden_layer_bias)
self.output_layer = NeuronLayer(num_outputs, output_layer_bias)
self.init_weights_from_inputs_to_hidden_layer_neurons(hidden_layer_weights)
self.init_weights_from_hidden_layer_neurons_to_output_layer_neurons(output_layer_weights)
def init_weights_from_inputs_to_hidden_layer_neurons(self, hidden_layer_weights):
weight_num = 0
for h in range(len(self.hidden_layer.neurons)):
for i in range(self.num_inputs):
if not hidden_layer_weights:
self.hidden_layer.neurons[h].weights.append(random.random())
else:
self.hidden_layer.neurons[h].weights.append(hidden_layer_weights[weight_num])
weight_num += 1
def init_weights_from_hidden_layer_neurons_to_output_layer_neurons(self, output_layer_weights):
weight_num = 0
for o in range(len(self.output_layer.neurons)):
for h in range(len(self.hidden_layer.neurons)):
if not output_layer_weights:
self.output_layer.neurons[o].weights.append(random.random())
else:
self.output_layer.neurons[o].weights.append(output_layer_weights[weight_num])
weight_num += 1
def inspect(self):
print('------')
print('* Inputs: {}'.format(self.num_inputs))
print('------')
print('Hidden Layer')
self.hidden_layer.inspect()
print('------')
print('* Output Layer')
self.output_layer.inspect()
print('------')
def feed_forward(self, inputs):
hidden_layer_outputs = self.hidden_layer.feed_forward(inputs)
return self.output_layer.feed_forward(hidden_layer_outputs)
def train(self, training_inputs, training_outputs):
self.feed_forward(training_inputs)
# 1. 输出神经元的值
pd_errors_wrt_output_neuron_total_net_input = [0] * len(self.output_layer.neurons)
for o in range(len(self.output_layer.neurons)):
# ∂E/∂zⱼ
pd_errors_wrt_output_neuron_total_net_input[o] = self.output_layer.neurons[o].calculate_pd_error_wrt_total_net_input(training_outputs[o])
# 2. 隐含层神经元的值
pd_errors_wrt_hidden_neuron_total_net_input = [0] * len(self.hidden_layer.neurons)
for h in range(len(self.hidden_layer.neurons)):
# dE/dyⱼ = Σ ∂E/∂zⱼ * ∂z/∂yⱼ = Σ ∂E/∂zⱼ * wᵢⱼ
d_error_wrt_hidden_neuron_output = 0
for o in range(len(self.output_layer.neurons)):
d_error_wrt_hidden_neuron_output += pd_errors_wrt_output_neuron_total_net_input[o] * self.output_layer.neurons[o].weights[h]
# ∂E/∂zⱼ = dE/dyⱼ * ∂zⱼ/∂
pd_errors_wrt_hidden_neuron_total_net_input[h] = d_error_wrt_hidden_neuron_output * self.hidden_layer.neurons[h].calculate_pd_total_net_input_wrt_input()
# 3. 更新输出层权重系数
for o in range(len(self.output_layer.neurons)):
for w_ho in range(len(self.output_layer.neurons[o].weights)):
# ∂Eⱼ/∂wᵢⱼ = ∂E/∂zⱼ * ∂zⱼ/∂wᵢⱼ
pd_error_wrt_weight = pd_errors_wrt_output_neuron_total_net_input[o] * self.output_layer.neurons[o].calculate_pd_total_net_input_wrt_weight(w_ho)
# Δw = α * ∂Eⱼ/∂wᵢ
self.output_layer.neurons[o].weights[w_ho] -= self.LEARNING_RATE * pd_error_wrt_weight
# 4. 更新隐含层的权重系数
for h in range(len(self.hidden_layer.neurons)):
for w_ih in range(len(self.hidden_layer.neurons[h].weights)):
# ∂Eⱼ/∂wᵢ = ∂E/∂zⱼ * ∂zⱼ/∂wᵢ
pd_error_wrt_weight = pd_errors_wrt_hidden_neuron_total_net_input[h] * self.hidden_layer.neurons[h].calculate_pd_total_net_input_wrt_weight(w_ih)
# Δw = α * ∂Eⱼ/∂wᵢ
self.hidden_layer.neurons[h].weights[w_ih] -= self.LEARNING_RATE * pd_error_wrt_weight
def calculate_total_error(self, training_sets):
total_error = 0
for t in range(len(training_sets)):
training_inputs, training_outputs = training_sets[t]
self.feed_forward(training_inputs)
for o in range(len(training_outputs)):
total_error += self.output_layer.neurons[o].calculate_error(training_outputs[o])
return total_error
class NeuronLayer:
def __init__(self, num_neurons, bias):
# 同一层的神经元共享一个截距项b
self.bias = bias if bias else random.random()
self.neurons = []
for i in range(num_neurons):
self.neurons.append(Neuron(self.bias))
def inspect(self):
print('Neurons:', len(self.neurons))
for n in range(len(self.neurons)):
print(' Neuron', n)
for w in range(len(self.neurons[n].weights)):
print(' Weight:', self.neurons[n].weights[w])
print(' Bias:', self.bias)
def feed_forward(self, inputs):
outputs = []
for neuron in self.neurons:
outputs.append(neuron.calculate_output(inputs))
return outputs
def get_outputs(self):
outputs = []
for neuron in self.neurons:
outputs.append(neuron.output)
return outputs
class Neuron:
def __init__(self, bias):
self.bias = bias
self.weights = []
def calculate_output(self, inputs):
self.inputs = inputs
self.output = self.squash(self.calculate_total_net_input())
return self.output
def calculate_total_net_input(self):
total = 0
for i in range(len(self.inputs)):
total += self.inputs[i] * self.weights[i]
return total + self.bias
# 激活函数sigmoid
def squash(self, total_net_input):
return 1 / (1 + math.exp(-total_net_input))
def calculate_pd_error_wrt_total_net_input(self, target_output):
return self.calculate_pd_error_wrt_output(target_output) * self.calculate_pd_total_net_input_wrt_input();
# 每一个神经元的误差是由平方差公式计算的
def calculate_error(self, target_output):
return 0.5 * (target_output - self.output) ** 2
def calculate_pd_error_wrt_output(self, target_output):
return -(target_output - self.output)
def calculate_pd_total_net_input_wrt_input(self):
return self.output * (1 - self.output)
def calculate_pd_total_net_input_wrt_weight(self, index):
return self.inputs[index]
# 文中的例子:
nn = NeuralNetwork(2, 2, 2, hidden_layer_weights=[0.15, 0.2, 0.25, 0.3], hidden_layer_bias=0.35, output_layer_weights=[0.4, 0.45, 0.5, 0.55], output_layer_bias=0.6)
for i in range(10000):
nn.train([0.05, 0.1], [0.01, 0.09])
print(i, round(nn.calculate_total_error([[[0.05, 0.1], [0.01, 0.09]]]), 9))
#另外一个例子,可以把上面的例子注释掉再运行一下:
# training_sets = [
# [[0, 0], [0]],
# [[0, 1], [1]],
# [[1, 0], [1]],
# [[1, 1], [0]]
# ]
# nn = NeuralNetwork(len(training_sets[0][0]), 5, len(training_sets[0][1]))
# for i in range(10000):
# training_inputs, training_outputs = random.choice(training_sets)
# nn.train(training_inputs, training_outputs)
# print(i, nn.calculate_total_error(training_sets))
图示例反向传播¶
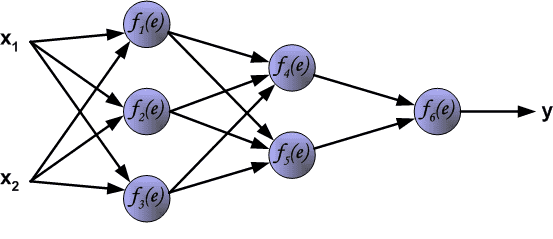
反向传播算法的多层神经网络的教学过程。为了说明这一点 处理如图所示的具有两个输入和一个输出的三层神经网络¶
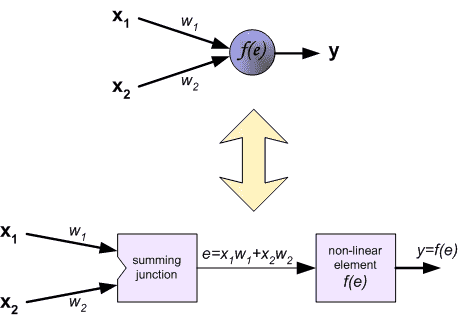
每个神经元由两个单元组成。第一个单元将权重系数和输入信号的乘积相加。第二个单元实现非线性函数,称为神经元激活函数。信号e为加法器输出信号, y=f(e)为非线性元件的输出信号。信号y也是神经元的输出信号。¶
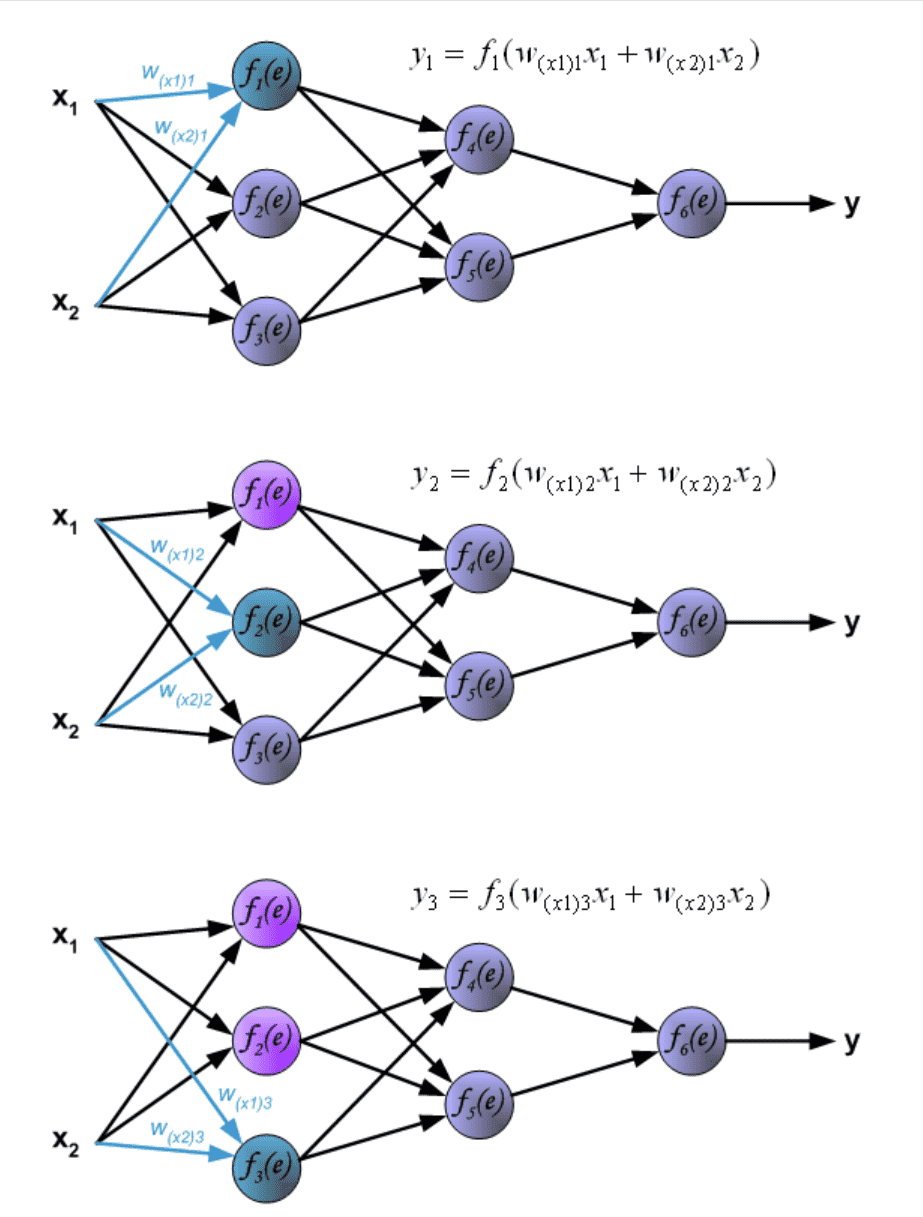
网络训练是一个迭代过程。在每次迭代中,使用训练数据集中的新数据来修改节点的权重系数。使用下述算法计算修改:每个训练步骤都强制从训练集的两个输入信号开始。在此阶段之后,我们可以确定每个网络层中每个神经元的输出信号值。下图说明了信号如何在网络中传播,符号
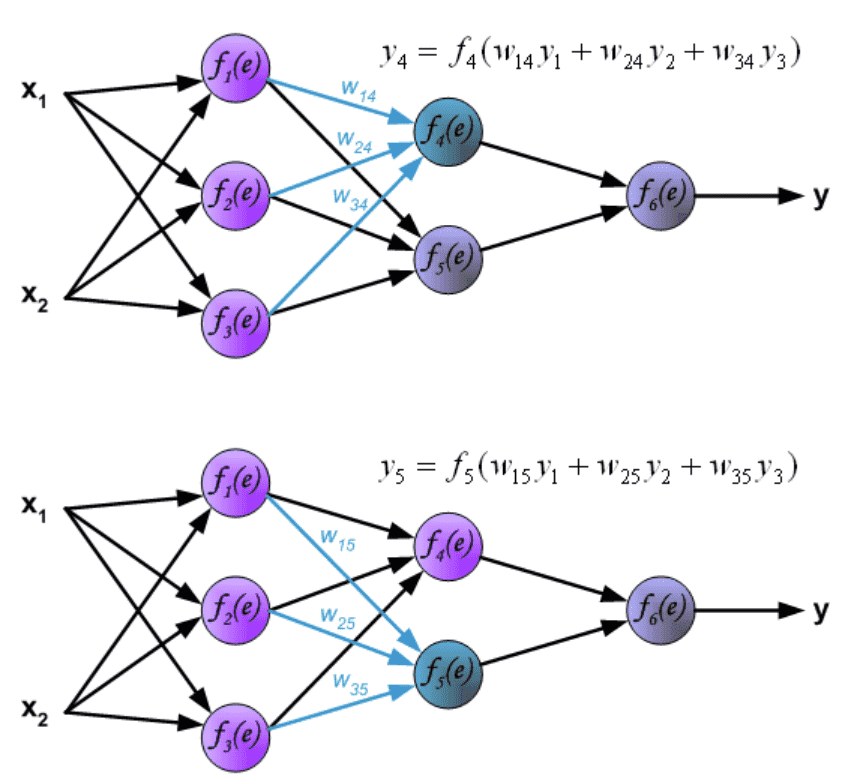
通过隐藏层传播信号。符号
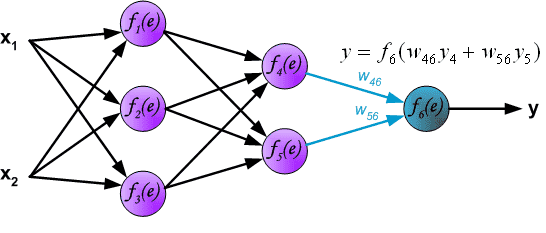
通过输出层传播信号。Propagation of signals through the output layer.¶
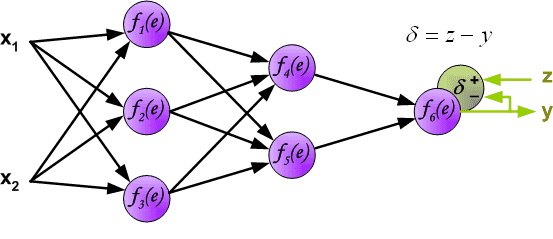
在下一个算法步骤中,将网络y的输出信号与训练数据集的目标值(label)进行比较。该差值称为输出层神经元的误差信号d 。¶
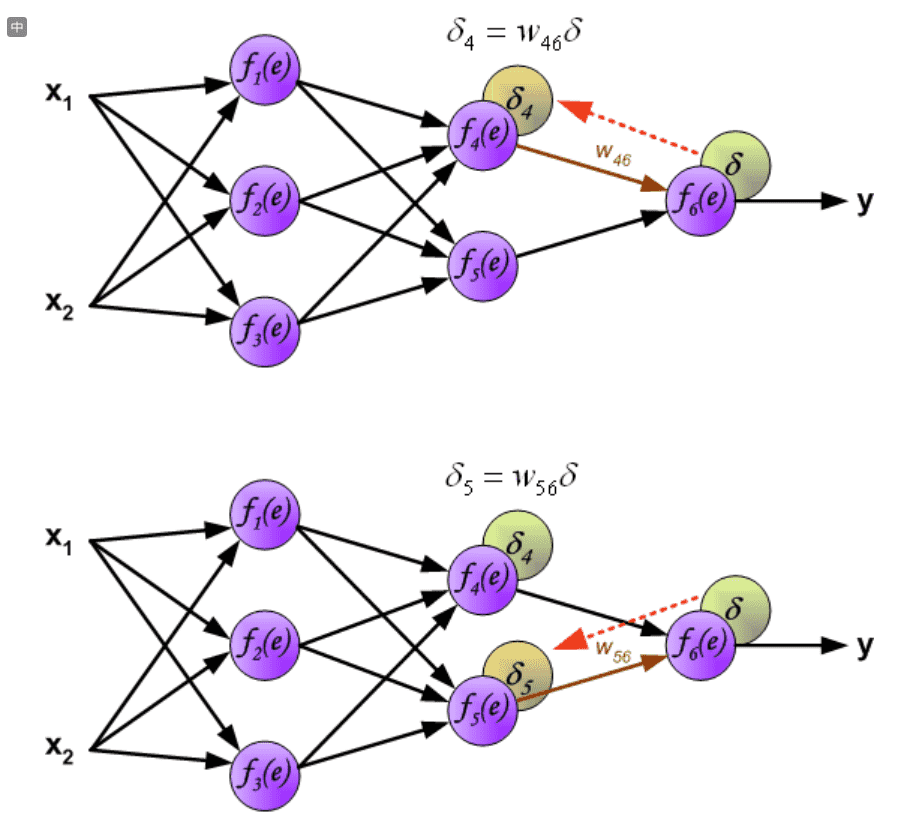
直接计算内部神经元的误差信号是不可能的,因为这些神经元的输出值是未知的。多年来,训练多结点网络的有效方法一直未知。直到八十年代中期,反向传播算法才被研究出来。这个想法是将误差信号d (在单个教学步骤中计算)传播回所有神经元,其输出信号是所讨论神经元的输入。¶
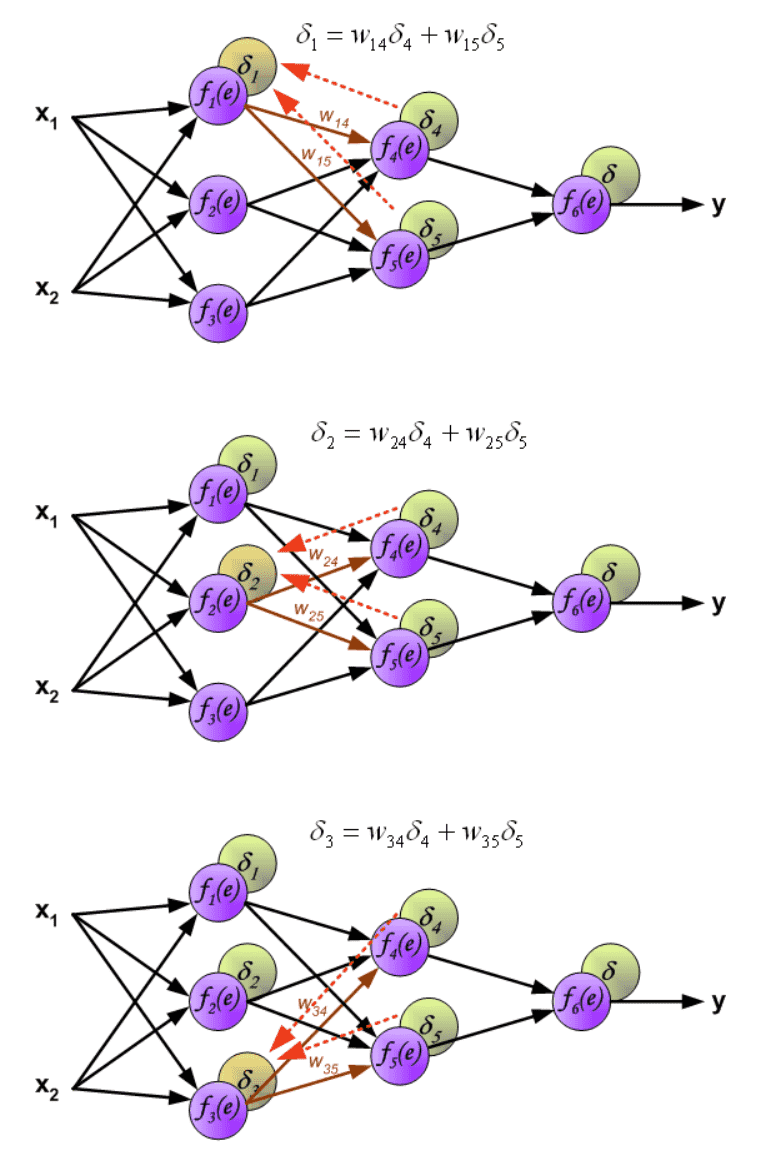
用于传播误差的权重系数
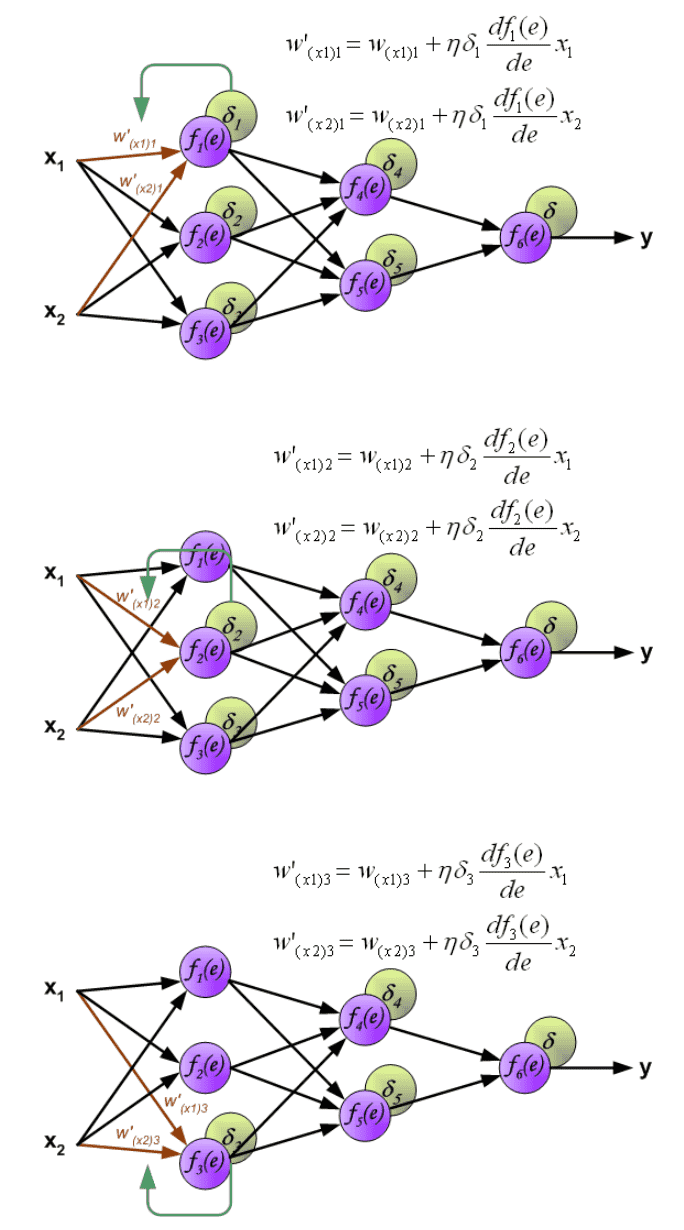
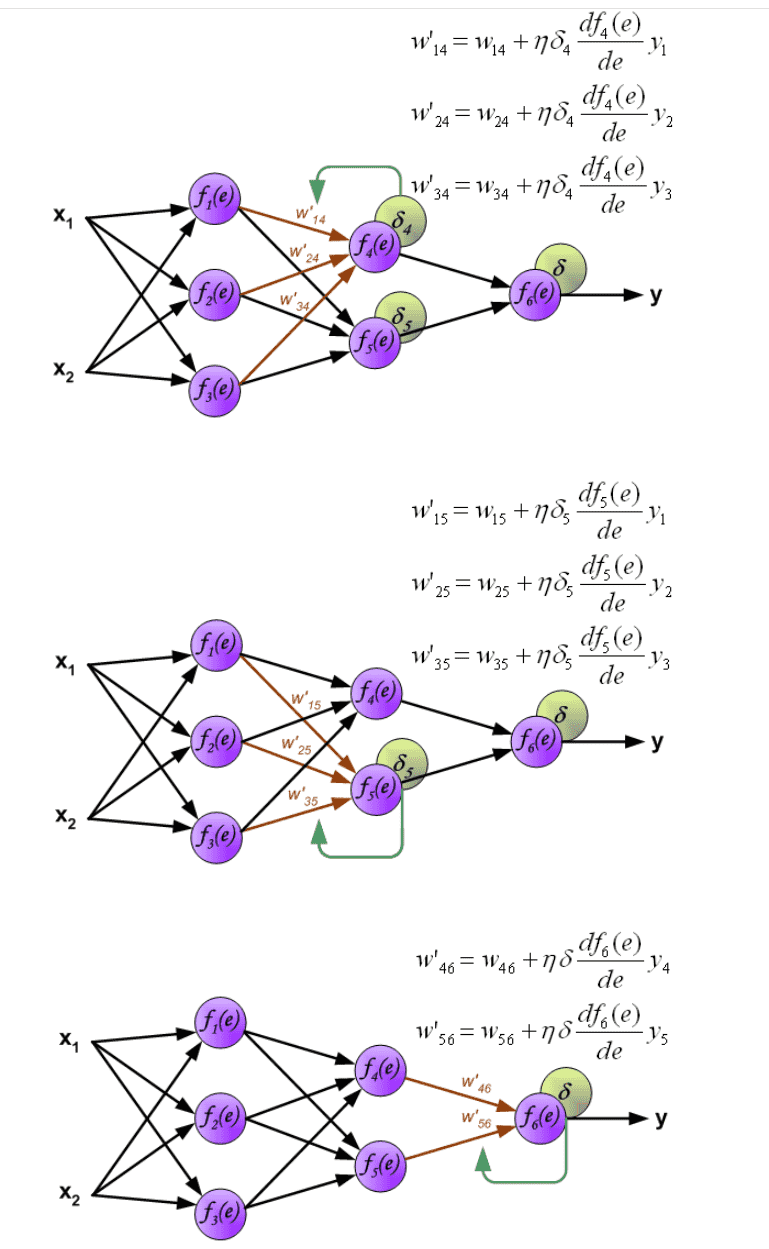
当计算每个神经元的误差信号时,可以修改每个神经元输入节点的权重系数。在如图公式中, df(e)/de 表示神经元激活函数的导数(其权重被修改)。¶
参考¶
Principles of training multi-layer neural network using backpropagation: http://galaxy.agh.edu.pl/~vlsi/AI/backp_t_en/backprop.html
[Deep Learning] 神经网络基础: https://www.cnblogs.com/maybe2030/p/5597716.html





