scaling law¶
Scaling laws(尺度定律)
.. warning:: 2019年,scaling laws,全国科学技术名词审定委员会审定发布的物理学名词: 标度律
备注
尺度定律(Scaling laws)是一种描述系统随着规模的变化而发生的规律性变化的数学表达。这些规律通常表现为一些可测量的特征随着系统大小的增加而呈现出一种固定的比例关系。
一种本质性的思维方式¶
标度律不仅是一个科学定律,更是一种本质性的思维方式。
蚂蚁可以负重比它重好多倍的东西,于是如果有一个和人一样的大蚂蚁,是不是也可以做到像蚂蚁一样的能力呢?答案是否定的。
假把蚂蚁等比例放大为原来的N倍,那么它的”体积”与“体重”就会变为原来的N^3倍;另一方面,腿的“横截面积”与“最大承重”会变为原来的N^2倍。也就是说,“体重”比“腿的最大承重”增长得快,总会支撑不住,把腿压折。
备注
动物不能按比例线性缩放:因为体积和重量是三维量,而横截面积是二维量。这种朴素快捷的分析思路,就是典型的“标度思路”。
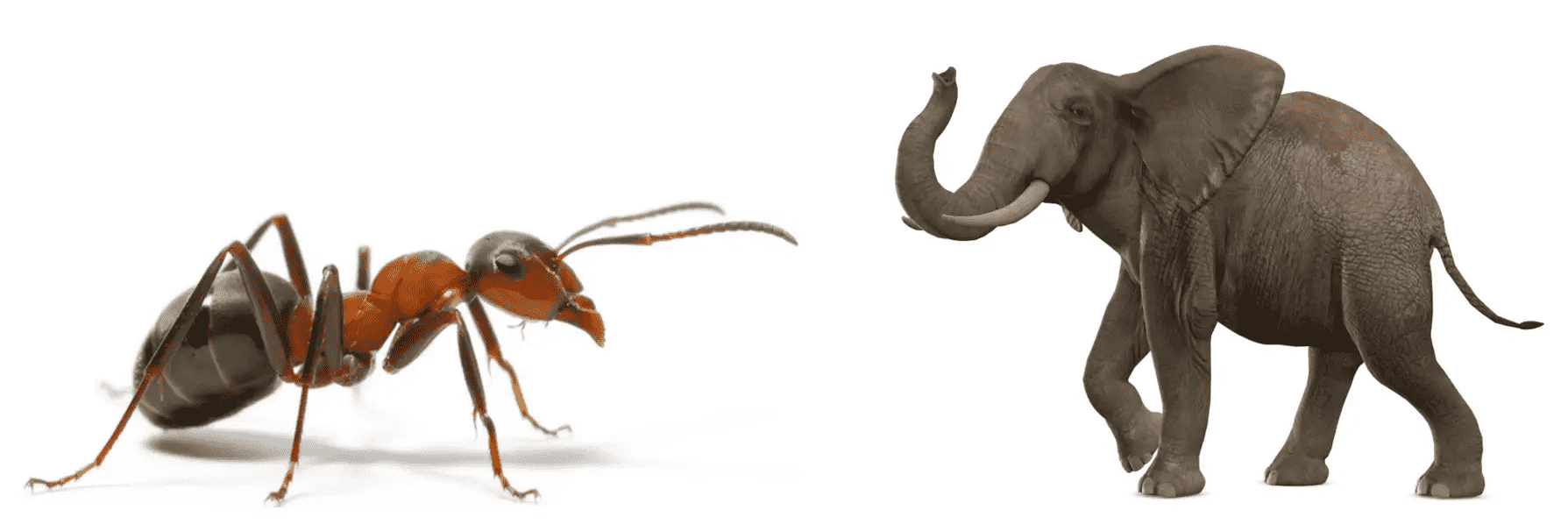
蚂蚁和大象的脚的粗细与体型的关系。
典型应用:大轮船更省燃料
假如把轮船放大为原来的N倍,那么它的”体积”与“载重”就会变为原来的N^3倍;另一方面,船的“横截面积”与“水的阻力”会变为原来的N^2倍;而燃料的消耗主要取决于水的阻力。
所以:轮船越大,运送单位载重所需要的燃料就越少。
备注
这种现象在经济学中,被称为“规模经济”(Economies of scale),表示规模增大时,效能的提高。
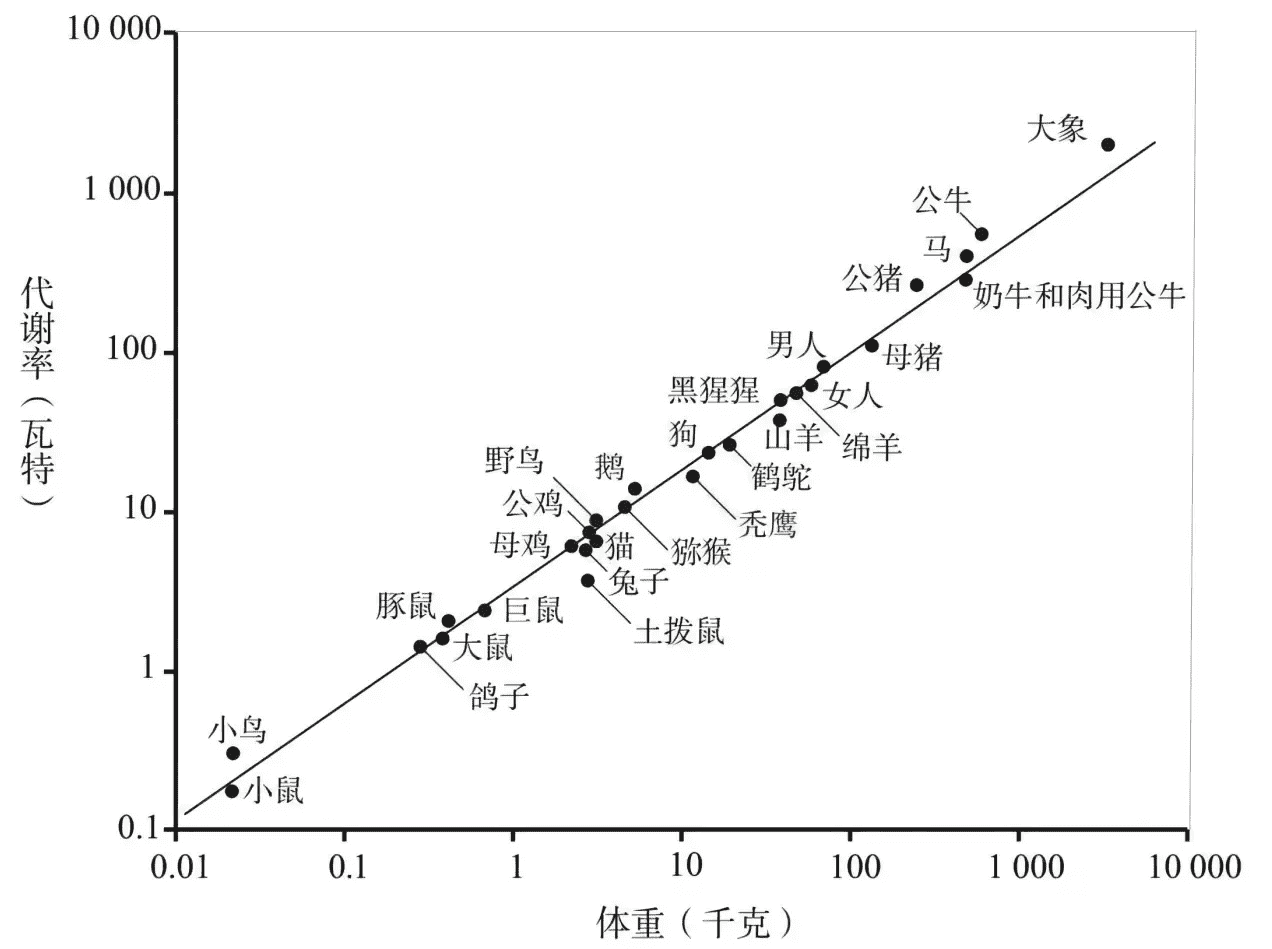
一张涵盖所有物种的’神奇线图’:把不同物种,以“体重”为横坐标,以“代谢率”为纵坐标,画在一个图中,图中所有动物物种都在一条直线上!
首先要解释一下,该图为“双对数图”,就是说X轴和Y轴都取了对数,这样就可以把不同尺度上的数据画在同一个图中了(注意观察坐标值)。
另外,何为代谢率?其实,代谢率就是生物的功率,也就是消耗能量的速率。比如,人的代谢率约为90瓦,跟一个灯泡差不多。从这个角度讲,生物本身是非常节约能量的。
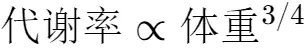
上图上的直线,用公式的表示:其中的“3/4”就是直线的斜率,这就是大名鼎鼎的“代谢标度律”,也称“克莱伯定律”。根据公式,大象的体重是老鼠的1万倍,但它的代谢率只老鼠的1000倍。很有意思,体重是1万倍的话,细胞数量也是1万倍呀;但是,总体的耗能却只有1000倍,这说明大象每个细胞的耗能只有老鼠的1/10!
各领域的应用¶
计算机科学¶
在计算机科学中,尤其是在机器学习和人工智能领域,scaling law 指的是模型性能随着训练数据量、模型复杂度(比如参数数量)增加时的表现。
OpenAI的研究者在2020年发现,大语言模型也遵循着尺度定律:大语言模型的尺度定律描述的是模型的性能 L ,模型的参数量大小 N ,训练模型的数据大小 D 以及训练模型使用的计算量 C 之间的关系。对于计算量 C ,模型参数量 N 和数据集大小 D ,当不受其他两个因素制约时,模型性能 L 与每个因素都呈现幂律关系。需要注意的是,大语言模型的尺度定律并非源于理论推导,而是基于经验性的实验分析。
物理¶
在物理学中,特别是凝聚态物理和统计物理,scaling law 描述的是在临界点附近系统的性质如何随着距离或时间尺度的变化而变化。这些定律帮助理解了相变过程中物理量的普适行为。
生物学¶
生物学中的 scaling law 主要关注生物体的生理特性与其体积或体重的关系。一个著名的例子是克莱伯定律(Kleiber’s law),它指出代谢率与体重的3/4次幂成正比
社会经济学¶
社会经济学领域也采用 scaling law 来分析城市规模、人口密度等与经济活动之间的关系。
例如,一些研究表明城市的人均创新产出与城市人口规模之间存在超线性关系,这意味着更大城市的人均创新产出会高于小城市。





