概率质量函数(Probability Mass Function, PMF)

  • 概率质量函数（PMF）是离散随机变量的一种基本概念，用来描述离散随机变量取特定值的概率分布。

  • 概率质量函数是离散随机变量的核心概念，清晰地描述了每个可能值的概率分布。通过 PMF，可以全面掌握离散随机变量的特性及其实际应用场景。

定义

对于离散随机变量 𝑋，其概率质量函数 𝑃(𝑋=𝑥) 满足以下条件：

1.P(X=x)≥02.∑x∈可能的取值P(X=x)=1

解释: P(X=x): 表示随机变量 𝑋 等于某一个具体值 𝑥 的概率 可能的取值是离散的，而不是连续的

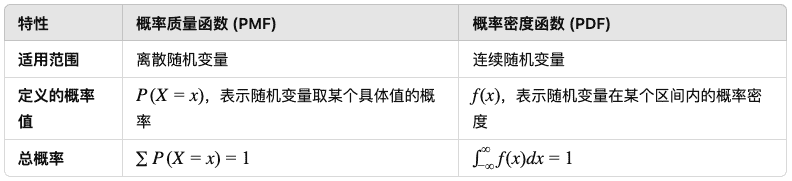
与概率密度函数的区别

直观理解

  • PMF 通过将离散的可能值与其对应的概率一一映射，帮助我们理解随机变量的分布情况。

  • 例如：

  • 投掷一个普通六面骰子时，随机变量 𝑋 表示掷出的点数，可能值为 {1,2,3,4,5,6}。

  • 每个值的概率是 𝑃(𝑋=𝑥)=1/6

  • PMF 描述了每个可能结果的发生概率。

常见离散分布的 PMF 示例

  1. 伯努利分布:

P(X=x)=px(1−p)1−x,x∈{0,1}

其中 p 是成功的概率。

  1. 二项分布:

P(X=k)=(nk)pk(1−p)n−k,k∈{0,1,…,n}

表示在 n 次试验中成功 k 次的概率。

  1. 几何分布:

P(X=k)=(1−p)k−1p,k∈{1,2,3,…}

表示第一次成功在第 k 次试验的概率。

  1. 泊松分布:

P(X=k)=λke−λk!,k∈{0,1,2,…}

用于描述单位时间或单位空间内某事件发生的次数。