8.3. ReLU(激活函数)¶
Rectified Linear Unit
特点:当输入为正数时输出等于输入,否则输出为 0。解决了梯度消失问题,使得训练更加稳定和快速。
公式:
从NN进入到DNN之后,直接的影响是:ReLU的大量应用。
ReLu是激活函数的一种:

就是这么简单的一个函数,在DNN时代代替了NN时代的激活函数王者:Sigmod,成了“调参侠”的最爱。
8.3.1. 为什么要用ReLU呢?¶
为什么要使用sigmoid,tanh,ReLU等非线性函数?是为了增加非线性呗!
深度学习的目的是用一堆神经元堆出一个函数大致的样子,然后通过大量的数据去反向拟合出这个函数的各个参数,最终勾勒出函数的完整形状。
那如果激活函数只是线性函数,那一层层的线性函数堆起来还是线性的,这肯定不行,这样整个网络表现能力有限,所以要引入非线性的激活函数进来。
8.3.2. ReLU的优势在哪儿呢¶
我们先来对比一下ReLU和他的老对手sigmoid:
ReLU函数:
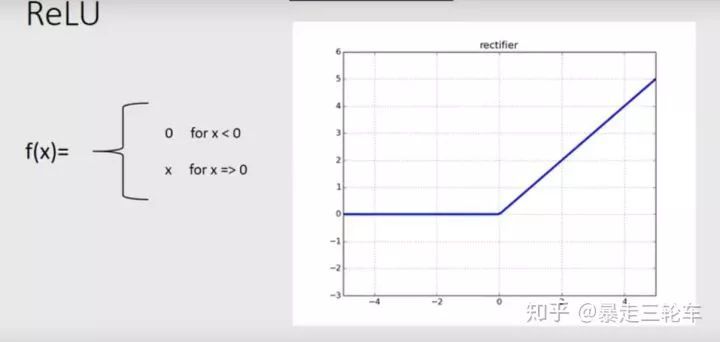
Sigmoid函数:
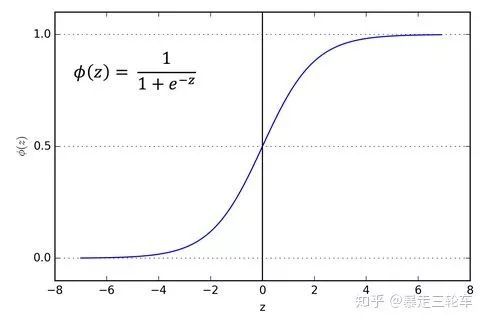
对比能看出来,sigmoid有一个“梯度消失”的问题
另一个ReLU很给力的地方就是稀疏度问题。就是我们希望每个神经元都能最大化的发挥它筛选的作用,符合某一个特征的中间值,使劲儿放大;不符合的,一刀切掉。反观sigmoid就要黏糊的多。这个函数是很对称很美,但它面对负的z值仍然剪不断理还乱,会输出一个小的激励值(tanh会好一些但仍不能避免),形成所谓的“稠密表示”。
最后的最后,ReLU运算速度快,这个很明显了,max肯定比幂指数快的多。
8.3.3. ReLU有什么弱点¶
当然,ReLU并不是完美的,它也存在被称为“dying ReLU”的问题——当某个ReLU神经元的输出为0时(输入小于0),它在反向传播时的梯度为0。这会导致该神经元“死亡”并影响一部分与之相连的神经元的训练效果。
为了解决这个问题,研究人员对ReLU进行了一些改进, Leaky ReLU 是其中比较知名的一种。
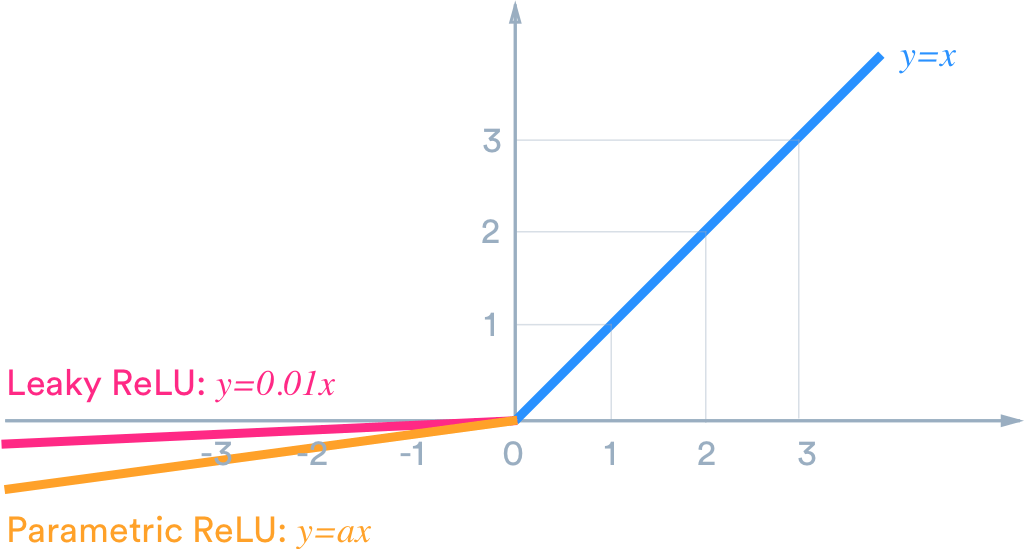
如图所示,Leaky ReLU将ReLU的 x < 0 部分修改成 0.01x,以此来让“死去”的神经元有机会恢复活力。
在实际应用中,因为不同ReLU变种之间的准确度区别很小,所以并不总是选用Leaky ReLU等变种。
对ReLU或其变种的选择可以根据模型的具体特性或实验结果决定。由于大多数深度学习类库都提供内建的ReLU模块,可以以较低的成本应对ReLU及其变种的性能差异。
此外,“dying ReLU”问题也可以通过降低学习率,加入bias等方式解决。
8.3.4. 常见的激活函数¶
torch.nn.log_softmax(input_vector, dim=0)
torch.nn.softmax(input_vector, dim=0)





