b-树¶
定义:B-树是一类树,包括B-树、B+树、B*树等,是一棵自平衡的搜索树,它类似普通的平衡二叉树,不同的一点是B-树允许每个节点有更多的子节点。B-树是专门为外部存储器设计的,如磁盘,它对于读取和写入大块数据有良好的性能,所以一般被用在文件系统及数据库中。
传统用来搜索的平衡二叉树有很多,如 AVL 树,红黑树等。这些树在一般情况下查询性能非常好,但当数据非常大的时候它们就无能为力了。原因当数据量非常大时,内存不够用,大部分数据只能存放在磁盘上,只有需要的数据才加载到内存中。一般而言内存访问的时间约为 50 ns,而磁盘在 10 ms 左右。速度相差了近 5 个数量级,磁盘读取时间远远超过了数据在内存中比较的时间。
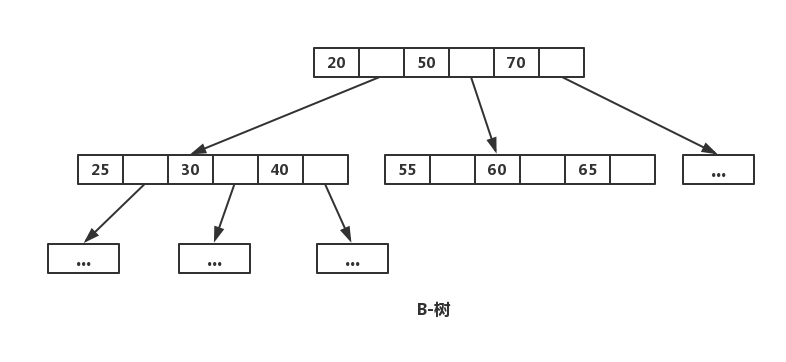
B 树又叫平衡多路查找树。一棵m阶的B 树的特性如下:
树中每个结点最多含有m-1个孩子(m>=2)
除根结点和叶子结点外,其它每个结点至少有[ceil(m / 2)]个孩子(其中ceil(x)是一个取上限的函数)
若根结点不是叶子结点,则至少有2个孩子
特殊情况:没有孩子的根结点,即根结点为叶子结点,整棵树只有一个根节点
所有叶子结点都出现在同一层,叶子结点不包含任何关键字信息
假如是m阶,则关键字最多有m-1个(这在页的分裂比较重要,后面会详细说),然后B树的数据是每个节点都会有的(这导致每个页可以存储的关键字数目变少,变相的导致树会变高,而树越高,磁盘寻道次数就可能越多,就越可能浪费时间)