主页

索引

模块索引

搜索页面

常用

重要

学习数据结构和算法，要学习它的由来、特性、适用的场景以及它能解决的问题。

定义:

从广义上讲，数据结构就是指一组数据的存储结构。算法就是操作数据的一组方法。
从狭义上讲，是指某些著名的数据结构和算法，比如队列、栈、堆、二分查找、动态规划等。

数据结构和算法是相辅相成的。
数据结构是为算法服务的，算法要作用在特定的数据结构之上。

10 个数据结构:

数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树

10 个算法:

递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法

时间复杂度

备注

大 O 时间复杂度表示法。大 O 时间复杂度实际上并不具体表示代码真正的执行时间，而是表示代码执行时间随数据规模增长的变化趋势，所以，也叫作渐进时间复杂度（asymptotic time complexity），简称时间复杂度。

三个比较实用的方法:

1. 只关注循环执行次数最多的一段代码
2. 加法法则：总复杂度等于量级最大的那段代码的复杂度
3. 乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

时间复杂度分两类:

多项式量级
    1. O(1)
    2. O(logn)、O(nlogn)
    3.  O(m+n)、O(m*n)
非多项式量级
    O (2^n) 和 O (n!)
    非多项式量级的算法问题叫作 NP（Non-Deterministic Polynomial，非确定多项式）问题
    非多项式时间复杂度的算法其实是非常低效的算法

空间复杂度

备注

空间复杂度全称就是渐进空间复杂度（asymptotic space complexity），表示算法的存储空间与数据规模之间的增长关系。

常见的空间复杂度就是:

O(1)、O(n)、O(n^2)



1. 最好情况时间复杂度（best case time complexity）
2. 最坏情况时间复杂度（worst case time complexity）
3. 平均情况时间复杂度（average case time complexity）
    加权平均值，也叫作期望值
4. 均摊时间复杂度（amortized time complexity）

数组-Array

数组（Array）是一种线性表数据结构。它用一组连续的内存空间，来存储一组具有相同类型的数据:

两个特点:
1. 线性表
2. 连续的内存空间和相同类型的数据

优点:
    一个堪称“杀手锏”的特性：“随机访问”
缺点:
    数组的很多操作变得非常低效，比如:
    要想在数组中删除、插入一个数据，为了保证连续性，就需要做大量的数据搬移工作。

数据结构:

1. 线性表（Linear List）
    顾名思义，线性表就是数据排成像一条线一样的结构。
    每个线性表上的数据最多只有前和后两个方向。
    其实除了数组，链表、队列、栈等也是线性表结构。
2. 非线性表
    比如二叉树、堆、图等。
    之所以叫非线性，是因为，在非线性表中，数据之间并不是简单的前后关系。

插入数据时间复杂度:

1. 在数组的末尾插入元素，那就不需要移动数据了，这时的时间复杂度为 O(1)
2. 在数组的开头插入元素，那所有的数据都需要依次往后移动一位，所以最坏时间复杂度是 O(n)
3. 如果在每个位置插入元素的概率是一样的，平均情况时间复杂度为 (1+2+...n)/n=O(n)

删除操作时间复杂度:

1. 删除数组末尾的数据，则最好情况时间复杂度为 O(1)
2. 删除开头的数据，则最坏情况时间复杂度为 O(n)
3. 平均情况时间复杂度也为 O(n)

备注

小技巧：JVM 标记清除垃圾回收算法的核心思想是『每次的删除操作并不是真正地搬移数据，只是记录数据已经被删除。当数组没有更多空间存储数据时，我们再触发执行一次真正的删除操作，这样就大大减少了删除操作导致的数据搬移。』

链表

缓存淘汰策略来决定。常见的策略有三种:

1. 先进先出策略 FIFO（First In，First Out）
2. 最少使用策略 LFU（Least Frequently Used）
3. 最近最少使用策略 LRU（Least Recently Used）

三种最常见的链表结构:

1. 单链表
2. 双向链表
3. 循环链表

循环链表是一种特殊的单链表:

它跟单链表唯一的区别就在尾结点。
单链表的尾结点指针指向空地址，表示这就是最后的结点了。
而循环链表的尾结点指针是指向链表的头结点。

例: 约瑟夫问题

双向链表:

单向链表只有一个方向，结点只有一个后继指针 next 指向后面的结点。
而双向链表，顾名思义，它支持两个方向，
每个结点不止有一个后继指针 next 指向后面的结点，
还有一个前驱指针 prev 指向前面的结点。

存储同样多的数据，双向链表要比单链表占用更多的内存空间

实战:5个常见的链表操作:

1. 单链表反转
2. 链表中环的检测
3. 两个有序的链表合并
4. 删除链表倒数第 n 个结点
5. 求链表的中间结点

练习题LeetCode对应编号：206，141，21，19，876

链表与数组

链表适合插入、删除，时间复杂度 O(1)
数组支持随机访问，根据下标随机访问的时间复杂度为 O(1)
排好序的数组，用二分查找，时间复杂度也是 O(logn)

栈

用数组实现的栈，我们叫作顺序栈，用链表实现的栈，我们叫作链式栈。 支持动态扩容的顺序栈 对于入栈操作来说，最好情况时间复杂度是 O(1)，最坏情况时间复杂度是 O(n)。将 K 个数据搬移均摊到 K 次入栈操作，入栈操作的均摊时间复杂度就为 O(1)。

1.栈在函数调用中的应用 操作系统给每个线程分配了一块独立的内存空间，这块内存被组织成“栈”这种结构，用来存储函数调用时的临时变量。每进入一个函数，就会将其中的临时变量作为栈帧入栈，当被调用函数执行完成，返回之后，将这个函数对应的栈帧出栈。

栈在表达式求值中的应用 编译器就是通过两个栈来实现的。其中一个保存操作数的栈，另一个是保存运算符的栈。我们从左向右遍历表达式，当遇到数字，我们就直接压入操作数栈；当遇到运算符，就与运算符栈的栈顶元素进行比较。 如果比运算符栈顶元素的优先级高，就将当前运算符压入栈；如果比运算符栈顶元素的优先级低或者相同，从运算符栈中取栈顶运算符，从操作数栈的栈顶取 2 个操作数，然后进行计算，再把计算完的结果压入操作数栈，继续比较。

后缀（逆波兰）表示法

栈在括号匹配中的应用 {[] ()[{}]}或[{()}([])]等都为合法格式，而{[}()]或[({)]为不合法的格式 当扫描到左括号时，则将其压入栈中；当扫描到右括号时，从栈顶取出一个左括号。如果能够匹配，比如“(”跟“)”匹配，“[”跟“]”匹配，“{”跟“}”匹配，则继续扫描剩下的字符串。如果扫描的过程中，遇到不能配对的右括号，或者栈中没有数据，则说明为非法格式。当所有的括号都扫描完成之后，如果栈为空，则说明字符串为合法格式；否则，说明有未匹配的左括号，为非法格式。

用栈实现浏览器的前进、后退功能

我们使用两个栈，X 和 Y，我们把首次浏览的页面依次压入栈 X，当点击后退按钮时，再依次从栈 X 中出栈，并将出栈的数据依次放入栈 Y。当我们点击前进按钮时，我们依次从栈 Y 中取出数据，放入栈 X 中。当栈 X 中没有数据时，那就说明没有页面可以继续后退浏览了。当栈 Y 中没有数据，那就说明没有页面可以点击前进按钮浏览了。

内存中的堆栈和数据结构堆栈 不是一个概念，可以说内存中的堆栈是真实存在的物理区，数据结构中的堆栈是抽象的数据存储结构。 内存空间在逻辑上分为三部分：代码区、静态数据区和动态数据区，动态数据区又分为栈区和堆区。 代码区：存储方法体的二进制代码。高级调度（作业调度）、中级调度（内存调度）、低级调度（进程调度）控制代码区执行代码的切换。 静态数据区：存储全局变量、静态变量、常量，常量包括final修饰的常量和String常量。系统自动分配和回收。 栈区：存储运行方法的形参、局部变量、返回值。由系统自动分配和回收。 堆区：new一个对象的引用或地址存储在栈区，指向该对象存储在堆区中的真实数据。

leetcode上关于栈的题目大家可以先做20,155,232,844,224,682,496.

队列

队列跟栈一样，也是一种操作受限的线性表数据结构。 最基本的操作也是两个：入队 enqueue ()，放一个数据到队列尾部；出队 dequeue () 额外特性的队列，比如:

1. 循环队列:
    最关键的是，确定好队空和队满的判定条件
    队列为空的判断条件仍然是 head == tail
    当队满时，(tail+1)%n=head
2. 阻塞队列:
    队列为空时: 从队头取数据会被阻塞。因为此时还没有数据可取，直到队列中有了数据才能返回
    队列已满时: 那么插入数据的操作就会被阻塞，直到队列中有空闲位置后再插入数据，然后再返回
    可以使用阻塞队列，轻松实现一个 “生产者 - 消费者模型”
3. 并发队列
    在多线程情况下，会有多个线程同时操作队列，这个时候就会存在线程安全问题
    线程安全的队列我们叫作并发队列。
    最简单直接的实现方式是直接在 enqueue ()、dequeue () 方法上加锁
    基于数组的循环队列，利用 CAS 原子操作，可以实现非常高效的并发队列
    这也是循环队列比链式队列应用更加广泛的原因

它们在很多偏底层系统、框架、中间件的开发中，起着关键性的作用。比如高性能队列 Disruptor、Linux 环形缓存，都用到了循环并发队列；Java concurrent 并发包利用 ArrayBlockingQueue 来实现公平锁等。

跟栈一样，队列可以用数组来实现，也可以用链表来实现。用数组实现的栈叫作顺序栈，用链表实现的栈叫作链式栈。同样，用数组实现的队列叫作顺序队列，用链表实现的队列叫作链式队列。

线程池没有空闲线程时，新的任务请求线程资源时，线程池该如何处理:

第一种是非阻塞的处理方式，直接拒绝任务请求；
另一种是阻塞的处理方式，将请求排队，等到有空闲线程时，取出排队的请求继续处理

基于链表和基于数组这两种实现方式对于排队请求又有什么区别:

1. 基于链表的实现方式，可以实现一个支持无限排队的无界队列（unbounded queue）
    但是可能会导致过多的请求排队等待，请求处理的响应时间过长。
    所以，针对响应时间比较敏感的系统，基于链表实现的无限排队的线程池是不合适的
2. 基于数组实现的有界队列（bounded queue），队列的大小有限
    所以线程池中排队的请求超过队列大小时，接下来的请求就会被拒绝，
    这种方式对响应时间敏感的系统来说，就相对更加合理。
    不过，设置一个合理的队列大小，也是非常有讲究的。
    队列太大导致等待的请求太多，队列太小会导致无法充分利用系统资源、发挥最大性能。

备注

队列可以应用在任何有限资源池中，用于排队请求，比如数据库连接池等。实际上，对于大部分资源有限的场景，当没有空闲资源时，基本上都可以通过 “队列” 这种数据结构来实现请求排队。

递归

递归需要满足的三个条件:

1. 一个问题的解可以分解为几个子问题的解
2. 这个问题与分解之后的子问题，除了数据规模不同，求解思路完全一样
3. 存在递归终止条件

写递归代码最关键的是:

1. 写出递推公式
2. 找到终止条件

写递归代码的关键就是找到如何将大问题分解为小问题的规律，并且基于此写出递推公式，
然后再推敲终止条件，最后将递推公式和终止条件翻译成代码。

排序算法

最经典的、最常用的:

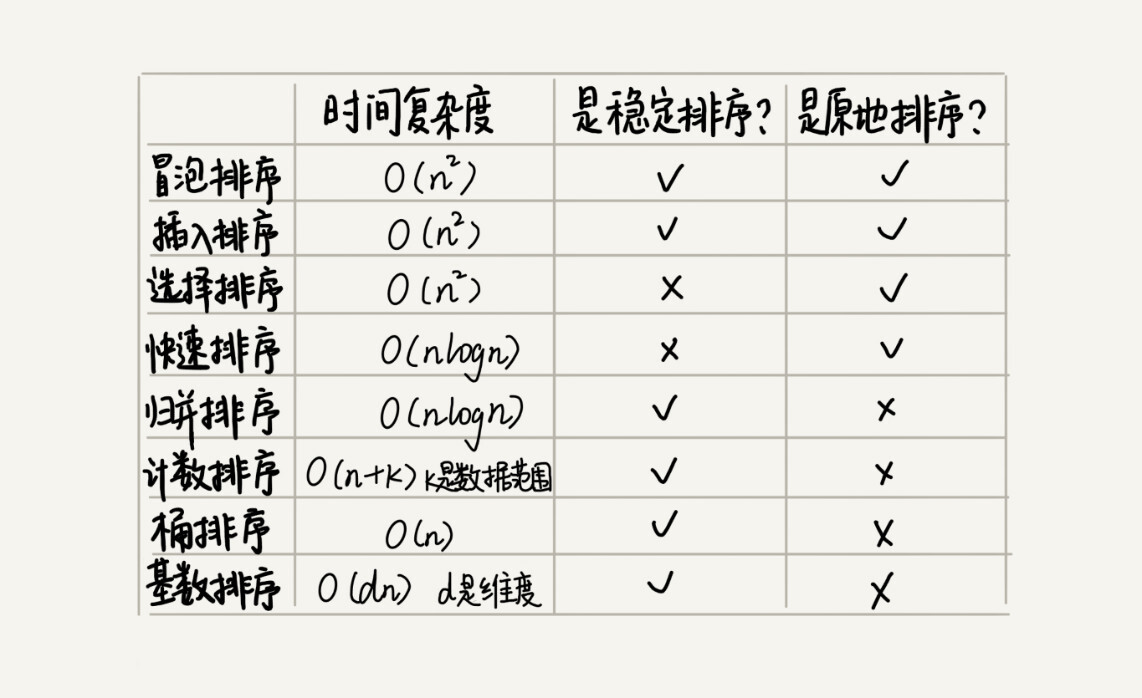
O(n^2), 基于比较: 冒泡排序、插入排序、选择排序
O(nlogn), 基于比较: 归并排序、快速排序
O(n), 不基于比较: 计数排序、基数排序、桶排序

不常用的:

猴子排序、睡眠排序、面条排序
希尔排序

一个重要的度量指标，稳定性:

这个概念是说，如果待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序不变

如果两个相同的数前后顺序没有改变，那我们就把这种排序算法叫作『稳定的排序算法』
如果前后顺序发生变化，那对应的排序算法就叫作『不稳定的排序算法』

有这个指标的原因是:
    在真正软件开发中，我们要排序的往往不是单纯的整数，而是一组对象，
    我们需要按照对象的某个 key 来排序
如:
    电商交易系统中的“订单”排序。订单有两个属性，一个是下单时间，另一个是订单金额。
    希望:
        1. 按照金额从小到大对订单数据排序
        2. 对于金额相同的订单，我们希望按照下单时间从早到晚有序
    操作:
        我们先按照下单时间给订单排序
        排序完成之后，我们用稳定排序算法，按照订单金额重新排序

冒泡排序-Bubble Sort

1. 原地排序算法
    只需要常量级的临时空间，空间复杂度为 O(1)
2. 稳定的排序算法
3. 时间复杂度:
    最好: O(n)
    最坏: O(n^2)
    平均: O(n^2)

有序度是数组中具有有序关系的元素对的个数
    有序元素对：a[i] <= a[j], 如果i < j
    例: 2, 4, 3, 1, 5, 6
        有序度为11
        (2, 4) (2, 3) (2, 5) (2, 6)
        (4, 5) (4, 6) (3, 5) (3, 6)
        (1, 5) (1, 6) (5, 6)
    例: 6, 5, 4, 3, 2, 1
        有序度为0
逆序度的定义正好跟有序度相反
    逆序元素对：a[i] > a[j], 如果i < j
    例: 2, 4, 3, 1, 5, 6
        逆序度为4
        (2, 1) (4, 3) (4, 1) (3, 1)
逆序度 = 满有序度 - 有序度

冒泡次数     冒泡结果        有序度
初使状态    2 4 3 1 5 6      11
第1次冒泡   2 3 1 4 5 6      13
第2次冒泡   2 1 3 4 5 6      14
第3次冒泡   1 2 3 4 5 6      15(满有序度)

冒泡排序包含两个操作原子，比较和交换。
每交换一次，有序度就加 1。
不管算法怎么改进，交换次数总是确定的，即为逆序度，也就是``n*(n-1)/2–初始有序度``

最坏情况下，初始状态的有序度是 0，所以要进行 n*(n-1)/2 次交换
最好情况下，初始状态的有序度是 n*(n-1)/2，就不需要进行交换

插入排序-Insertion Sort

1. 原地排序算法
2. 稳定的排序算法
3. 时间复杂度:
    最好(正序): 时间复杂度为 O(n)
    最坏(倒序): 时间复杂度为 O(n^2)
    平均: O(n^2)

将数组中的数据分为两个区间，已排序区间和未排序区间
插入算法的核心思想是:
    取未排序区间中的元素，在已排序区间中找到合适的插入位置将其插入，
    并保证已排序区间数据一直有序。
    重复这个过程，直到未排序区间中元素为空，算法结束。

插入排序也包含两种操作，一种是元素的比较，一种是元素的移动
移动次数就等于逆序度:

 插入排序结果          移动元素个数
2 | 4 3 1 5 6              0
2 4 | 3 1 5 6              0
2 3 4 | 1 5 6              1
1 2 3 4 | 5 6              3

选择排序-Selection Sort

1. 原地排序算法
2. 非稳定排序算法
    如: 5，8，5，2，9
    第一次找到最小元素 2，与第一个 5 交换位置，
    那第一个 5 和中间的 5 顺序就变了，所以就不稳定了
3. 时间复杂度:
    最好情况时间复杂度、最坏情况和平均情况时间复杂度都为 O(n^2)

分已排序区间和未排序区间
每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾

插入排序比冒泡排序更受欢迎的原因:

冒泡排序的数据交换要比插入排序的数据移动要复杂，
冒泡排序需要 3 个赋值操作，而插入排序只需要 1 个

冒泡排序中数据的交换操作：
if (a[j] > a[j+1]) { // 交换
   int tmp = a[j];
   a[j] = a[j+1];
   a[j+1] = tmp;
   flag = true;
}
插入排序中数据的移动操作：
if (a[j] > value) {
  a[j+1] = a[j];  // 数据移动
} else {
  break;
}

归并排序-Merge Sort

备注

归并排序和快速排序都用到了分治思想，非常巧妙。我们可以借鉴这个思想，来解决非排序的问题，比如：如何在 O(n) 的时间复杂度内查找一个无序数组中的第 K 大元素？

备注

分治算法一般都是用递归来实现的。分治是一种解决问题的处理思想，递归是一种编程技巧

1. 空间复杂度:
    非原地排序算法
    空间复杂度就是 O(n)
2. 稳定排序算法
3. 时间复杂度:
    最好情况、最坏情况，还是平均情况，时间复杂度都是O(nlogn)

时间复杂度计算过程:

不仅递归求解的问题可以写成递推公式，递归代码的时间复杂度也可以写成递推公式:
    求解问题 a 的时间是 T(a)，求解问题 b、c 的时间分别是 T(b) 和 T(c):
    T(a) = T(b) + T(c) + K
    其中 K 等于将两个子问题 b、c 的结果合并成问题 a 的结果所消耗的时间
2个点:
    1. merge() 函数合并两个有序子数组的时间复杂度是 O(n)
    2. n 个元素进行归并排序需要的时间是 T(n)，那分解成两个子数组排序的时间都是 T(n/2)
归并排序的时间复杂度的计算公式:
    T(1) = C；   n=1时，只需要常量级的执行时间，所以表示为C。
    T(n) = 2*T(n/2) + n； n>1
计算过程:
    T(n) = 2*T(n/2) + n
     = 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2*n
     = 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n
     = 8*(2*T(n/16) + n/8) + 3*n = 16*T(n/16) + 4*n
     ......
     = 2^k * T(n/2^k) + k * n
     ......
终止条件:
    T(n/2^k)=T(1)=C
    即: n/2^k=1
    即: k=log2n
T(n)=2^log2n * T(1) + log2n*n = Cn+nlog2n
用大 O 标记法来表示的话，T(n) 就等于 O(nlogn)。
所以归并排序的时间复杂度是 O(nlogn)

快速排序算法-Quicksort

快排的思想是这样的:

如果要排序数组中下标从 p 到 r 之间的一组数据，
我们选择 p 到 r 之间的任意一个数据作为 pivot（分区点）
遍历 p 到 r 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot 放到中间

1. 空间复杂度:
    原地排序算法
    空间复杂度就是 O(1)
2. 非稳定排序算法
3. 时间复杂度:
    最好情况时间复杂度都是O(nlogn)
    最坏情况是 O(n^2)
    大部分情况下的时间复杂度都可以做到 O(nlogn)

伪代码:

// 快速排序，A是数组，n表示数组的大小
quick_sort(A, n) {
  quick_sort_c(A, 0, n-1)
}
// 快速排序递归函数，p,r为下标
quick_sort_c(A, p, r) {
  if p >= r then return

  q = partition(A, p, r) // 获取分区点
  quick_sort_c(A, p, q-1)
  quick_sort_c(A, q+1, r)
}

partition(A, p, r) {
  pivot := A[r]
  i := p
  for j := p to r-1 do {
    if A[j] < pivot {
      swap A[i] with A[j]
      i := i+1
    }
  }
  swap A[i] with A[r]
  return i

备注

归并排序的处理过程是由下到上的，先处理子问题，然后再合并。而快排正好相反，它的处理过程是由上到下的，先分区，然后再处理子问题。归并排序虽然是稳定的、时间复杂度为 O(nlogn) 的排序算法，但是它是非原地排序算法。

时间复杂度计算过程:

T(1) = C；   n=1时，只需要常量级的执行时间，所以表示为C
T(n) = 2*T(n/2) + n； n>1
// 公式成立的前提是每次分区操作，我们选择的 pivot 都很合适，正好能将大区间对等地一分为二

最极端的情况需要进行大约 n 次分区操作，才能完成快排的整个过程
    每次分区我们平均要扫描大约 n/2 个元素，
    这种情况下，快排的时间复杂度就从 O(nlogn) 退化成了 O(n2)

用快排解决第 K 大元素:

计算过程:
1. 分成了三部分，A[0...p-1]、A[p]、A[p+1...n-1]
2. 如果 p+1=K，那 A[p]就是要求解的元素；
   如果 K>p+1, 说明第 K 大元素出现在 A[p+1...n-1]区间
   否则说明第 K 大元素出现在 A[0...p-1]区间

时间复杂度是 O(n):
第一次分区查找，我们需要对大小为 n 的数组执行分区操作，需要遍历 n 个元素。
第二次分区查找，我们只需要对大小为 n/2 的数组执行分区操作，需要遍历 n/2 个元素。
依次类推，分区遍历元素的个数分别为、n/2、n/4、n/8、n/16.……直到区间缩小为 1
即:
n+n/2+n/4+n/8+...+1=2n-1

用普通解决第 K 大元素:

每次取数组中的最小值，将其移动到数组的最前面，
    然后在剩下的数组中继续找最小值，以此类推，执行 K 次
时间复杂度就并不是 O(n) 了，而是 O(K * n)
    当 K 等于 n/2 或者 n 时，这种最坏情况下的时间复杂度就是 O(n2) 了

备注

现在你有 10 个接口访问日志文件，每个日志文件大小约 300MB，每个文件里的日志都是按照时间戳从小到大排序的。你希望将这 10 个较小的日志文件，合并为 1 个日志文件，合并之后的日志仍然按照时间戳从小到大排列。如果处理上述排序任务的机器内存只有 1GB，你有什么好的解决思路，能“快速”地将这 10 个日志文件合并吗？

利用哨兵减少了交换两个元素的复杂步骤:

private static void quickSort(int[] a, int head, int tail) {

    int low = head;
    int high = tail;
    int pivot = a[low];
    if (low < high) {

        while (low<high) {
            while (low < high && pivot <= a[high]) high--;
            a[low] = a[high];
            while (low < high && pivot >= a[low]) low++;
            a[high]=a[low];
        }
        a[low] = pivot;

        if(low>head+1) quickSort(a,head,low-1);
        if(high<tail-1) quickSort(a,high+1,tail);
    }

}

线性排序-Linear sort

三种时间复杂度是 O(n) 的排序算法：桶排序、计数排序、基数排序。因为这些排序算法的时间复杂度是线性的，所以我们把这类排序算法叫作线性排序（Linear sort）

桶排序-Bucket sort

如果要排序的数据有 n 个，我们把它们均匀地划分到 m 个桶内，每个桶里就有 k=n/m 个元素。每个桶内部使用快速排序，时间复杂度为 O(k * logk)。m 个桶排序的时间复杂度就是 O(m * k * logk)，因为 k=n/m，所以整个桶排序的时间复杂度就是 O(n*log(n/m))。当桶的个数 m 接近数据个数 n 时，log(n/m) 就是一个非常小的常量，这个时候桶排序的时间复杂度接近 O(n)。

桶排序对要排序数据的要求是非常苛刻的:

1. 要排序的数据需要很容易就能划分成 m 个桶
2. 数据在各个桶之间的分布是比较均匀的

备注

桶排序比较适合用在外部排序中。所谓的外部排序就是数据存储在外部磁盘中，数据量比较大，内存有限，无法将数据全部加载到内存中。

计数排序-Counting sort

计数排序其实是桶排序的一种特殊情况。当要排序的 n 个数据，所处的范围并不大的时候，比如最大值是 k，我们就可以把数据划分成 k 个桶。每个桶内的数据值都是相同的，省掉了桶内排序的时间。

50万考生排序，满分是 900 分，最小是 0 分，这个数据的范围很小，所以我们可以分成 901 个桶，对应分数从 0 分到 900 分。

排序过程:

要排序的数组: A[8]
中间的桶: C[6]
排序后的数组: R[8]

要排序的数组: A[8] = 2，5，3，0，2，3，0，3
考生的成绩从 0 到 5 分，我们使用大小为 6 的数组 C[6]表示桶
    C[6] = 2 0 2 3 0 1
对 C[6]数组顺序求和
    C2[6] = 2 2 4 7 0 8
从后到前依次扫描数组 A。比如:
    当扫描到 3 时，我们知道 C[3] 的值 7
    则: R[7-1]=R[6]=3
    然后 C[3] = C[3]-1
    ...

备注

计数排序只能用在数据范围不大的场景中，如果数据范围 k 比要排序的数据 n 大很多，就不适合用计数排序了。而且，计数排序只能给非负整数排序，如果要排序的数据是其他类型的，要将其在不改变相对大小的情况下，转化为非负整数。

基数排序-Radix sort

规律:

假设要比较两个手机号码 a，b 的大小，如果在前面几位中，a 手机号码已经比 b 手机号码大了，那后面的几位就不用看了

11位手机号码排序:

先按照最后一位来排序手机号码
然后，再按照倒数第二位重新排序
以此类推，最后按照第一位重新排序
经过 11 次排序之后，手机号码就都有序了

备注

【小技巧】要排序的数据并不都是等长的情况，可以把所有的数据补齐到相同长度，如:单词位数不够的可以在后面补“0”

排序优化

https://img.zhaoweiguo.com/knowledge/images/algorithms/sort-complex.jpg

快速排序如何选择分区点:

1. 三数取中法
2. 随机法

快速排序是用递归来实现的,要警惕堆栈溢出:

1. 限制递归深度。一旦递归过深，超过了我们事先设定的阈值，就停止递归
2. 通过在堆上模拟实现一个函数调用栈，手动模拟递归压栈、出栈的过程

备注

实际在使用时可以使用多种排序算法，如 glic 中的 qsort 函数：1.排序数据量小时使用归并排序，2.数据量大时使用快速排序，3.在快速排序的过程中，当要排序的区间中，元素的个数小于等于 4 时，qsort() 就退化为插入排序。

二分查找

二分查找:

时间复杂度是 O(logn)

着重强调一下容易出错的 3 个地方:

1. 循环退出条件
2. mid 的取值
    mid=(low+high)/2 这种写法是有问题的。
    因为如果 low 和 high 比较大的话，两者之和就有可能会溢出
    改进的方法是将 mid 的计算方式写成 low+(high-low)/2。
    进一步性能优化: 可以将这里的除以 2 操作转化成位运算 low+((high-low)>>1)
3. low 和 high 的更新

限制:

1. 依赖的是顺序表结构，简单点说就是数组
2. 针对的是有序数据
3. 数据量太小不适合二分查找
4. 数据量太大也不适合二分查找

十个二分九个错:

唐纳德·克努特（Donald E.Knuth）在《计算机程序设计艺术》的第 3 卷《排序和查找》中说到：
“尽管第一个二分查找算法于 1946 年出现，然而第一个完全正确的二分查找算法实现直到 1962 年才出现。”

最简单的二分查找写起来确实不难，但是，二分查找的变形问题就没那么好写了

4 个变形问题:

1. 查找第一个值等于给定值的元素
2. 查找最后一个值等于给定值的元素
3. 查找第一个大于等于给定值的元素
4. 查找最后一个小于等于给定值的元素

注: 有重复数据的情形下

快速定位出一个 IP 地址的归属地:

示例:
    [202.102.133.0, 202.102.133.255]  山东东营市
    [202.102.135.0, 202.102.136.255]  山东烟台
    [202.102.156.34, 202.102.157.255] 山东青岛
    [202.102.48.0, 202.102.48.255] 江苏宿迁
    [202.102.49.15, 202.102.51.251] 江苏泰州
    [202.102.56.0, 202.102.56.255] 江苏连云港
将起始地址，按照对应的整型值的大小关系，从小到大进行排序。
    IP 地址可以转化为 32 位的整型数。
问题就转化为第4个变形问题:
    在有序数组中，查找最后一个小于等于某个给定值的元素

备注

凡是用二分查找能解决的，绝大部分我们更倾向于用散列表或者二叉查找树。即便是二分查找在内存使用上更节省，但是毕竟内存如此紧缺的情况并不多。二分查找更适合用在“近似”查找问题，在这类问题上，二分查找的优势更加明显。比如这几种变体问题

变体的二分查找算法写起来非常烧脑，很容易因为细节处理不好而产生 Bug，这些容易出错的细节有:

1. 终止条件
2. 区间上下界更新方法
3. 返回值选择

  • leetcode 33题

随机访问

顺序访问:

链表在内存中不是按顺序存放的，而是通过指针连在一起，
为了访问某一元素，必须从链头开始顺着指针才能找到某一个元素。

随机访问:

Sequential Access
数组在内存中是按顺序存放的，可以通过下标直接定位到某一个元素存放的位置。

跳表-Skip list

插入、删除、查找操作，时间复杂度都是 O(logn)
空间复杂度是 O(n)
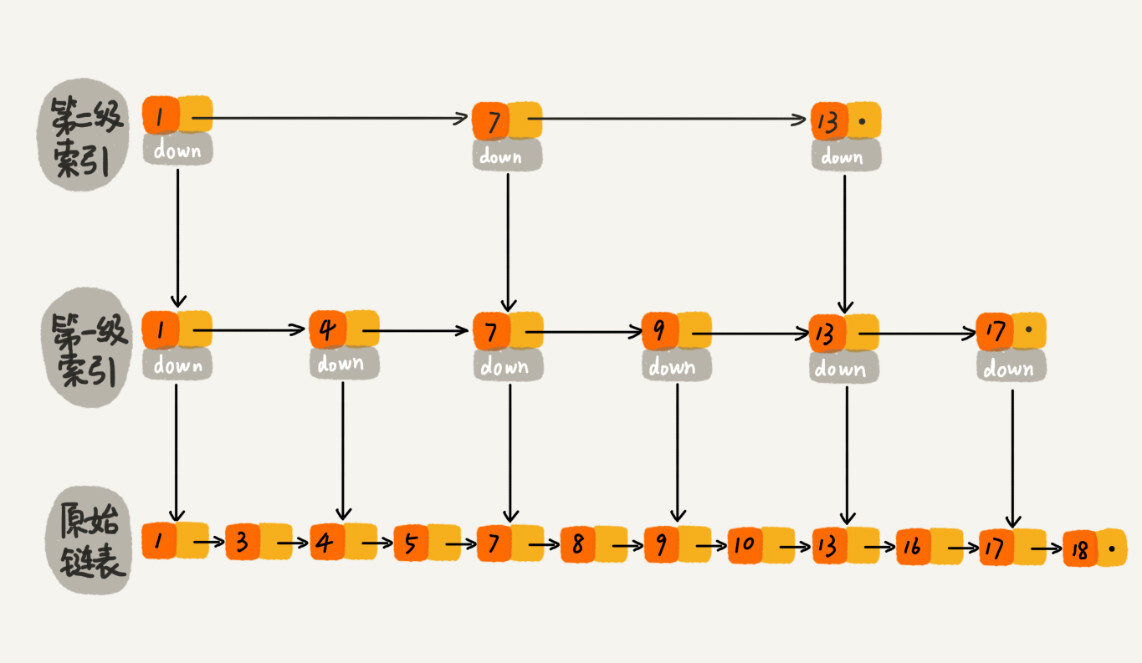
https://img.zhaoweiguo.com/knowledge/images/algorithms/skip-list1.jpg

这种链表加多级索引的结构，就是跳表

备注

作为一种动态数据结构，我们需要某种手段来维护索引与原始链表大小之间的平衡。红黑树、AVL 树这样平衡二叉树，你就知道它们是通过左右旋的方式保持左右子树的大小平衡，而跳表是通过随机函数来维护前面提到的“平衡性”。

为什么 Redis 要用跳表来实现有序集合，而不是红黑树:

Redis 中的有序集合支持的核心操作主要有下面这几个:
    1. 插入一个数据；
    2. 删除一个数据；
    3. 查找一个数据；
    4. 按照区间查找数据（比如查找值在[100, 356]之间的数据）；
    5. 迭代输出有序序列
操作1235红黑树也可以完成，时间复杂度跟跳表是一样的
但是，操作4红黑树的效率没有跳表高

散列表-Hash Table

备注

散列表用的是数组支持按照下标随机访问数据的特性，所以散列表其实就是数组的一种扩展，由数组演化而来。

散列表两个核心问题:

1. 散列函数设计
2. 散列冲突解决

散列函数设计的三点基本要求:

1. 散列函数计算得到的散列值是一个非负整数
2. 如果 key1 = key2，那 hash(key1) == hash(key2)
3. 如果 key1 ≠ key2，那 hash(key1) ≠ hash(key2)

散列冲突解决方法:

1. 开放寻址法-open addressing
2. 链表法-chaining

  1. 开放寻址法-open addressing:

    a. 线性探测-Linear Probing
    在散列表中查找元素的过程有点儿类似插入过程。
    我们通过散列函数求出要查找元素的键值对应的散列值，然后比较数组中下标为散列值的元素和要查找的元素。
    如果相等，则说明就是我们要找的元素；否则就顺序往后依次查找。
    如果遍历到数组中的空闲位置，还没有找到，就说明要查找的元素并没有在散列表中。
    注意:
        删除操作稍微有些特别，不能单纯地把要删除的元素设置为空
        可以将删除的元素，特殊标记为 deleted
b. 二次探测-Quadratic probing
    跟线性探测很像，线性探测每次探测的步长是 1，
        它探测的下标序列就是 hash(key)+0，hash(key)+1，hash(key)+2……
    而二次探测探测的步长就变成了原来的“二次方”，也就是说，
        它探测的下标序列就是 hash(key)+0，hash(key)+1^2，hash(key)+2^2……
c. 双重散列-Double hashing
    意思就是不仅要使用一个散列函数。
    我们使用一组散列函数 hash1(key)，hash2(key)，hash3(key)……
    我们先用第一个散列函数，如果计算得到的存储位置已经被占用，再用第二个散列函数，
    依次类推，直到找到空闲的存储位置

优点:
    1. 散列表中的数据都存储在数组中，可以有效地利用 CPU 缓存加快查询速度
    2. 这种方法实现的散列表，序列化起来比较简单

缺点:
    1. 删除数据的时候比较麻烦，需要特殊标记已经删除掉的数据
    2. 冲突的代价更高:
        所以，使用开放寻址法解决冲突的散列表，装载因子的上限不能太大。
        这也导致这种方法比链表法更浪费内存空间

备注

当数据量比较小、装载因子小的时候，适合采用开放寻址法

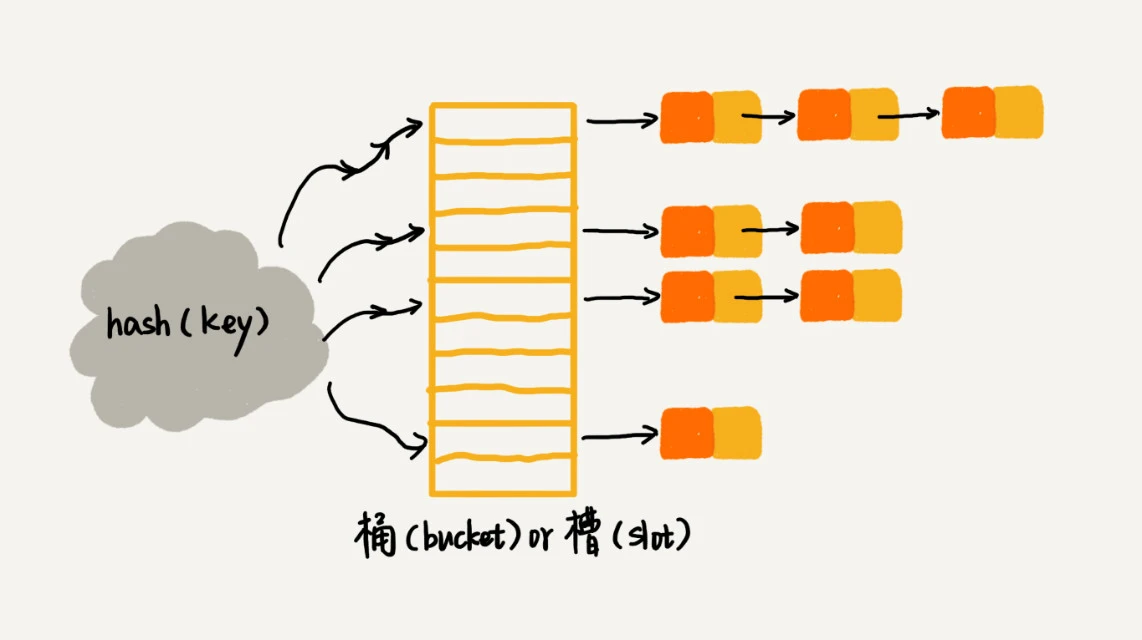
  1. 链表法-chaining:

    链表法是一种更加常用的散列冲突解决办法，相比开放寻址法，它要简单很多

优点:
    a. 对内存的利用率比开放寻址法要高
    b. 对大装载因子的容忍度更高

缺点:
    a. 链表中的结点是零散分布在内存中的，不是连续的
        所以对 CPU 缓存是不友好的，这方面对于执行效率也有一定的影响
    b. 比较消耗内存的，还有可能会让内存的消耗翻倍
        若存储的是大对象，即要存储的对象的大小远大于一个指针的大小（4 个字节或者 8 个字节）
        那链表中指针的内存消耗在大对象面前就可以忽略了

备注

基于链表的散列冲突处理方法比较适合存储大对象、大数据量的散列表，而且，比起开放寻址法，它更加灵活，支持更多的优化策略，比如用红黑树代替链表。

装载因子(load factor)用来表示空位的多少:

装载因子是数组的装载率。反映的是数组填满的程度。装载因子越大，说明冲突越多。
散列表的装载因子=填入表中的元素个数/散列表的长度
装载因子越大，说明空闲位置越少，冲突越多，散列表的性能会下降。
https://img.zhaoweiguo.com/knowledge/images/algorithms/hash-table-chaining1.webp

好的散列函数:

1. 散列函数的设计不能太复杂
    过于复杂的散列函数，势必会消耗很多计算时间，也就间接地影响到散列表的性能
2. 散列函数生成的值要尽可能随机并且均匀分布
    这样才能避免或者最小化散列冲突，而且即便出现冲突，
    散列到每个槽里的数据也会比较平均，不会出现某个槽内数据特别多的情况

散列函数的设计方法:

1. 数据分析法: 取手机号的后四位作为散列值
2. 将单词中每个字母的ASCII 码值“进位”相加，然后再跟散列表的大小求余、取模
3. 其他: 直接寻址法、平方取中法、折叠法、随机数法

动态扩容:

当散列表的装载因子超过某个阈值时，就需要进行扩容

如何避免低效的扩容:
1. “一次性”扩容的机制
    先进行扩容，再插入数据
    缺点: 扩容时，插入数据就会变得很慢，甚至会无法接受
2. 分批扩容
    将扩容操作穿插在插入操作的过程中，分批完成
    操作:
    对于插入操作，先将新数据插入新散列表中，并且从老的散列表中拿出一个数据放入到新散列表
    对于查询操作，先从新散列表中查找，如果没有找到，再去老的散列表中查找

工业级的散列表应该具有哪些特性:

1. 支持快速地查询、插入、删除操作
2. 内存占用合理，不能浪费过多的内存空间
3. 性能稳定，极端情况下，散列表的性能也不会退化到无法接受的情况

如何实现这样一个工业级的散列表:

1. 设计一个合适的散列函数
2. 定义装载因子阈值，并且设计动态扩容策略
3. 选择合适的散列冲突解决方法

散列表和链表组合

LRU 缓存淘汰算法

一个缓存（cache）系统主要包含下面这几个操作:

1. 往缓存中添加一个数据
2. 从缓存中删除一个数据
3. 在缓存中查找一个数据

说明: 这三个操作都需要「查找」操作
如果单纯地采用链表的话，时间复杂度只能是 O(n)
如果我们将散列表和链表两种数据结构组合使用，可以将这三个操作的时间复杂度都降低到 O(1)
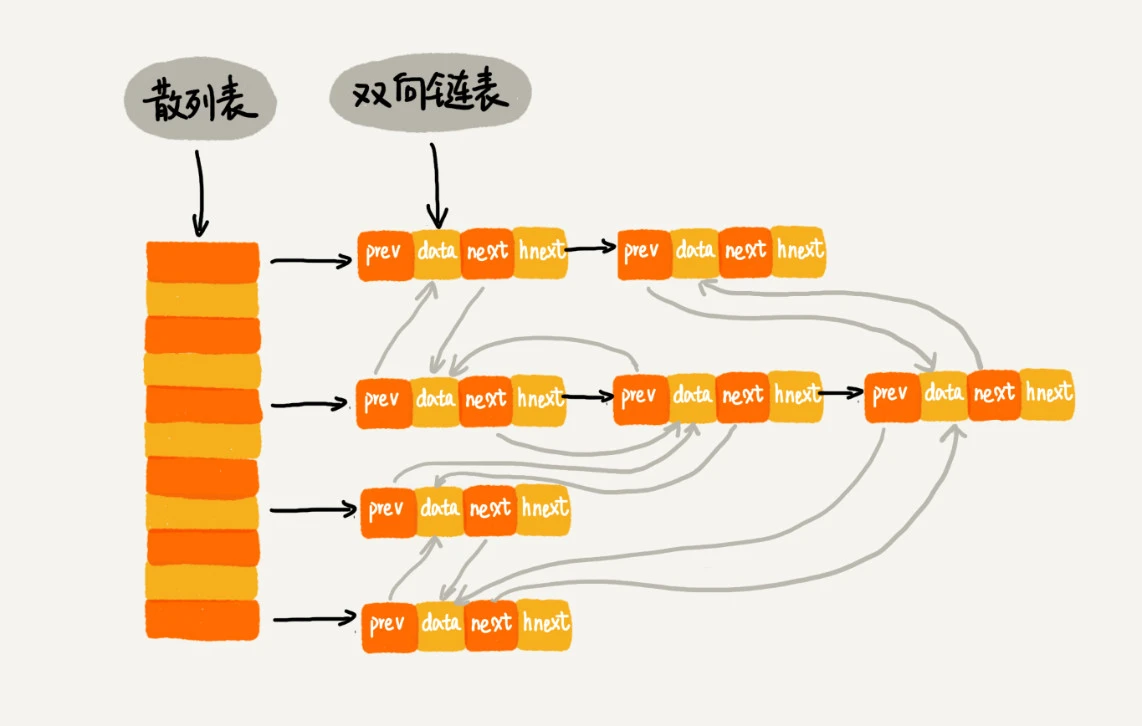
https://img.zhaoweiguo.com/knowledge/images/algorithms/hash-table-chaining2.webp

散列表这种数据结构虽然支持非常高效的数据插入、删除、查找操作，但是散列表中的数据都是通过散列函数打乱之后无规律存储的。也就说，它无法支持按照某种顺序快速地遍历数据。如果希望按照顺序遍历散列表中的数据，那我们需要将散列表中的数据拷贝到数组中，然后排序，再遍历。 因为散列表是动态数据结构，不停地有数据的插入、删除，所以每当我们希望按顺序遍历散列表中的数据的时候，都需要先排序，那效率势必会很低。为了解决这个问题，我们将散列表和链表（或者跳表）结合在一起使用。

哈希算法

一个优秀的哈希算法:

1. 从哈希值不能反向推导出原始数据（所以哈希算法也叫单向哈希算法）
2. 对输入数据非常敏感，哪怕原始数据只修改了一个 Bit，最后得到的哈希值也大不相同
3. 散列冲突的概率要很小，对于不同的原始数据，哈希值相同的概率非常小
4. 哈希算法的执行效率要尽量高效，针对较长的文本，也能快速地计算出哈希值

哈希算法的应用:

1. 安全加密
    鸽巢原理（也叫抽屉原理）
2. 唯一标识
    用于检测两文件是否完全一样
    如: 百度网盘的文件秒传功能
3. 数据校验
    用于检测文件是否被篡改
4. 散列函数
5. 负载均衡
6. 数据分片
7. 分布式存储

一致性哈希算法

备注

[基本思想]假设我们有 k 个机器，数据的哈希值的范围是 [0, MAX]。我们将整个范围划分成 m 个小区间（m 远大于 k），每个机器负责 m/k 个小区间。当有新机器加入的时候，我们就将某几个小区间的数据，从原来的机器中搬移到新的机器中。这样，既不用全部重新哈希、搬移数据，也保持了各个机器上数据数量的均衡。

树

定义:

父节点、子节点、兄弟节点
叶子节点或者叶节点、根节点

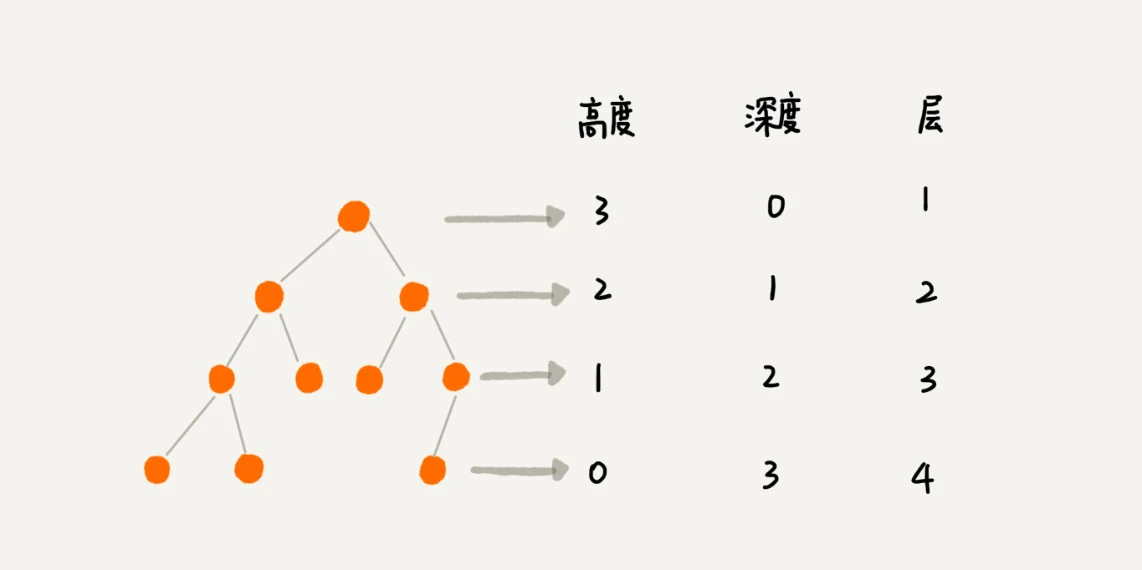
三个比较相似的概念:

1. 高度: Height
    节点到叶子节点的最长路径(边数)
2. 深度: Depth
    根节点到这个节点所经历的边数
3. 层: Level
    结点深度+1

树的高度=根结点的高度
https://img.zhaoweiguo.com/knowledge/images/algorithms/tree1.webp

二叉树-Binary Tree

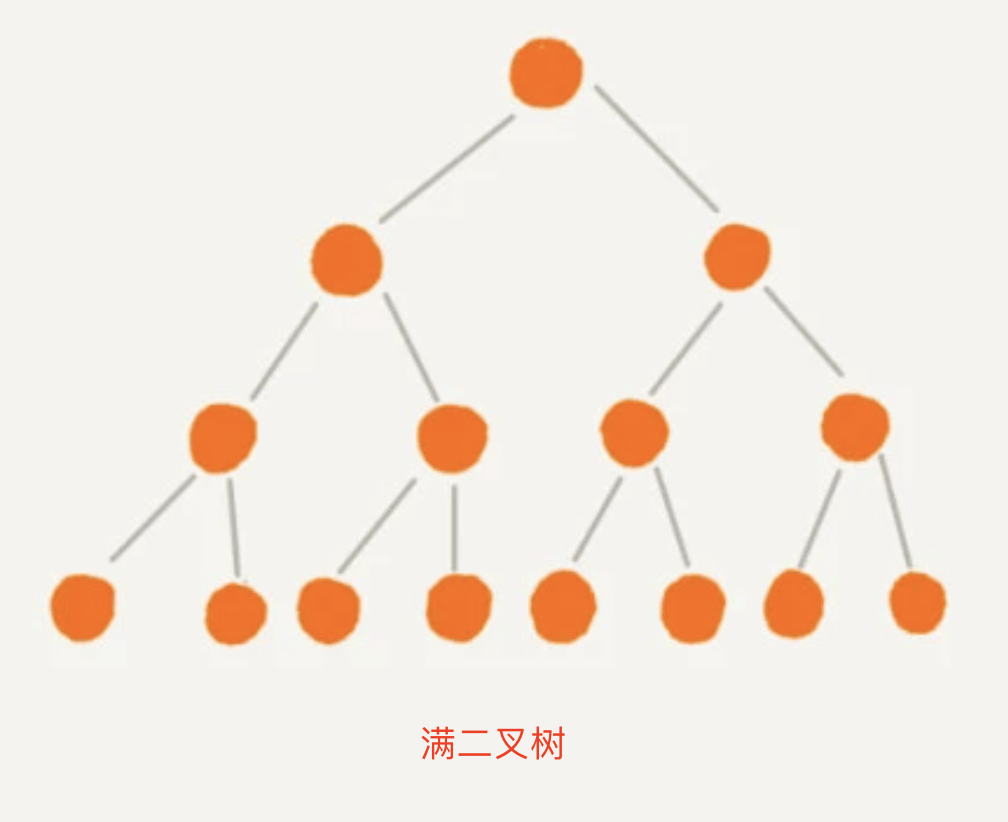
满二叉树:

叶子节点全都在最底层，除了叶子节点之外，每个节点都有左右两个子节点
https://img.zhaoweiguo.com/knowledge/images/algorithms/binary-tree1.png

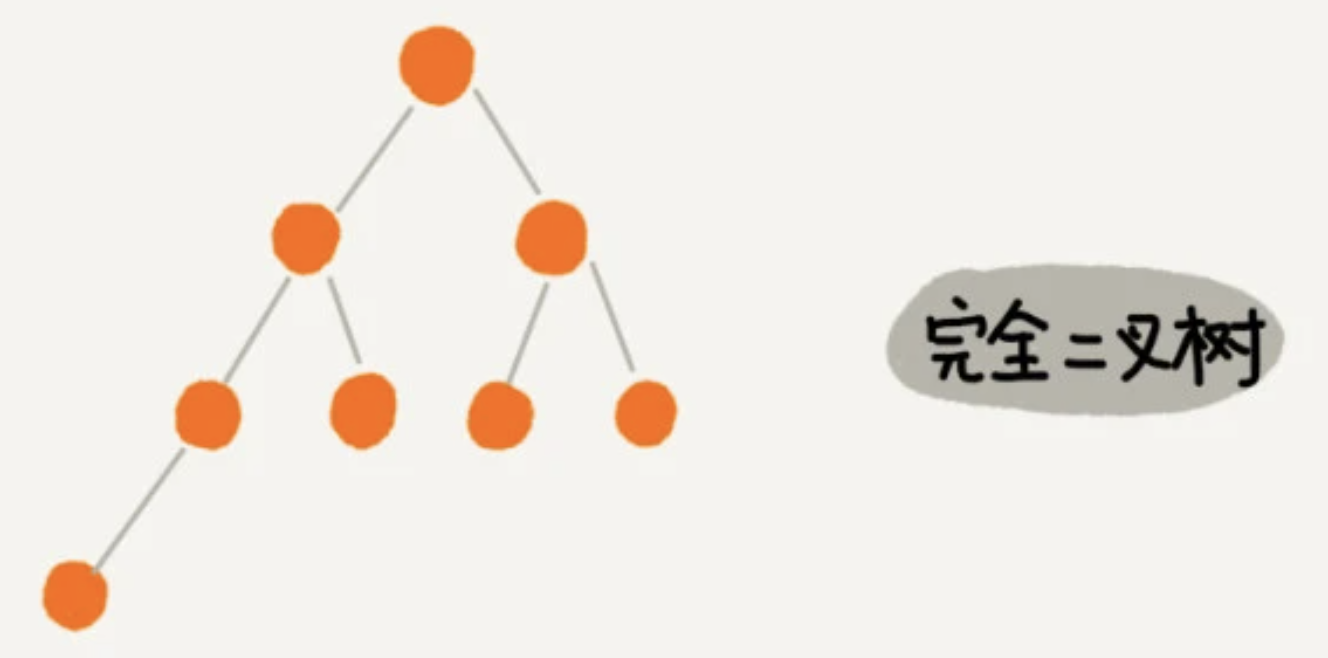
完全二叉树:

叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，
并且除了最后一层，其他层的节点个数都要达到最大
https://img.zhaoweiguo.com/knowledge/images/algorithms/binary-tree2.png

两种方法:

1. 一种是基于指针或者引用的二叉链式存储法
2. 一种是基于数组的顺序存储法

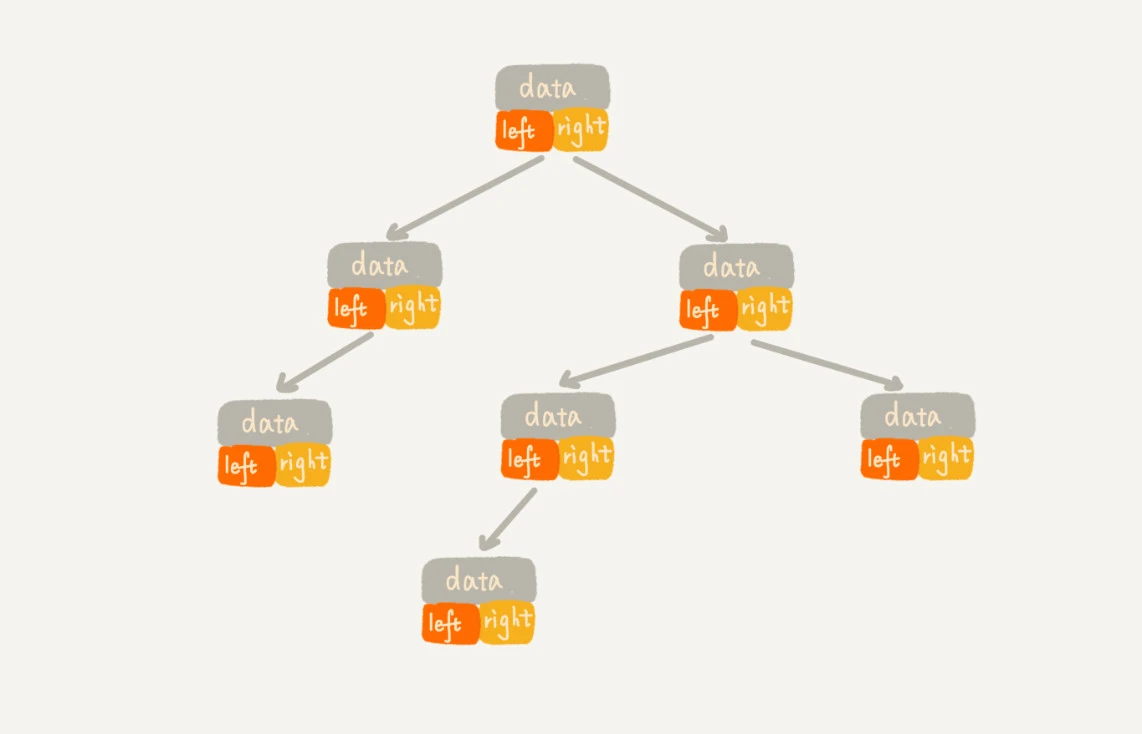
  1. 链式存储法:

    每个节点有三个字段，其中一个存储数据，另外两个是指向左右子节点的指针。
我们只要拎住根节点，就可以通过左右子节点的指针，把整棵树都串起来。
这种存储方式我们比较常用。大部分二叉树代码都是通过这种结构来实现的。
https://img.zhaoweiguo.com/knowledge/images/algorithms/binary-tree3.webp

  1. 顺序存储法:

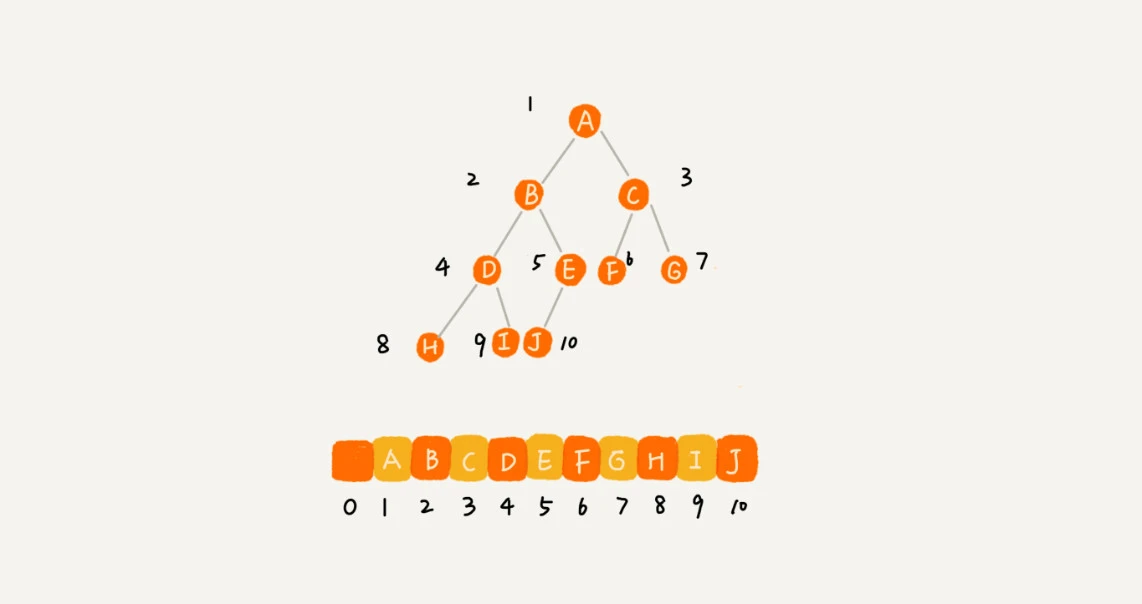
    把根节点存储在下标 i = 1 的位置，
左子节点存储在下标 2 * i = 2 的位置，
右子节点存储在 2 * i + 1 = 3 的位置。

以此类推，B 节点的:
左子节点存储在 2 * i = 2 * 2 = 4 的位置
右子节点存储在 2 * i + 1 = 2 * 2 + 1 = 5 的位置
https://img.zhaoweiguo.com/knowledge/images/algorithms/binary-tree4.webp

备注

如果某棵二叉树是一棵完全二叉树，那用数组存储无疑是最节省内存的一种方式。堆其实就是一种完全二叉树，最常用的存储方式就是数组。

二叉树的遍历

经典的方法有三种(DFS, 深度优先):

1. 前序遍历
    对于树中的任意节点来说，先打印这个节点，然后再打印它的左子树，最后打印它的右子树
2. 中序遍历
    对于树中的任意节点来说，先打印它的左子树，然后再打印它本身，最后打印它的右子树
3. 后序遍历
    对于树中的任意节点来说，先打印它的左子树，然后再打印它的右子树，最后打印这个节点本身

二叉查找树-Binary Search Tree

也叫二叉搜索树
也叫二叉排序树
为了实现快速查找而生的

二叉查找树要求:

在树中的任意一个节点:
其左子树中的每个节点的值，都要小于这个节点的值，
而右子树节点的值都大于这个节点的值

基本操作:

1. 二叉查找树的查找操作
2. 二叉查找树的插入操作
3. 二叉查找树的删除操作
    分三种情况:
    a. 要删除的节点没有子节点
    b. 要删除的节点只有一个子节点
    c. 要删除的节点有两个子节点
        找到这个节点的右子树中的最小节点，把它替换到要删除的节点上。
        然后再删除掉这个最小节点
4. 二叉查找树的其他操作
    支持快速地查找最大节点和最小节点、前驱节点和后继节点

支持重复数据的二叉查找树:

1. 第一种方法比较容易。
    二叉查找树中每一个节点不仅会存储一个数据，
    因此我们通过链表和支持动态扩容的数组等数据结构，把值相同的数据都存储在同一个节点上。
2. 第二种方法比较不好理解，不过更加优雅。
    每个节点仍然只存储一个数据。
    在查找插入位置的过程中，如果碰到一个节点的值，与要插入数据的值相同，
    我们就将这个要插入的数据放到这个节点的右子树，
    也就是说，把这个新插入的数据当作大于这个节点的值来处理。

不管操作是插入、删除还是查找，时间复杂度其实都跟树的高度成正比，也就是 O(height) 完全二叉树的高度小于等于 log2n

相对散列表，二叉查找树有什么优势:

1. 散列表中的数据是无序存储的，如果要输出有序的数据，需要先进行排序
2. 散列表扩容耗时很多，而且当遇到散列冲突时，性能不稳定
    尽管二叉查找树的性能不稳定
    但是平衡二叉查找树的性能非常稳定，时间复杂度稳定在 O(logn)
3. 散列表的查找等操作并不一定快:
    尽管散列表的查找等操作的时间复杂度是常量级的，
    但因为哈希冲突的存在，这个常量不一定比 logn 小，
    所以实际的查找速度可能不一定比 O(logn) 快。
    加上哈希函数的耗时，也不一定就比平衡二叉查找树的效率高
4. 散列表的构造比二叉查找树要复杂，需要考虑的东西很多
    比如散列函数的设计、冲突解决办法、扩容、缩容等。
    平衡二叉查找树只需要考虑平衡性这一个问题，而且这个问题的解决方案比较成熟、固定
5. 浪费一定的存储空间
    为了避免过多的散列冲突，散列表装载因子不能太大，
    特别是基于开放寻址法解决冲突的散列表

平衡二叉查找树

备注

二叉树中任意一个节点的左右子树的高度相差不能大于 1。红黑树的代码实现应该是最复杂的一个了，需要关注左旋、右旋。

  • 最先被发明的平衡二叉查找树是AVL 树

  • Splay Tree（伸展树）

  • Treap（树堆）

红黑树-Red-Black Tree

  • R-B Tree

  • 是一种不严格的平衡二叉查找树

红黑树中的节点，一类被标记为黑色，一类被标记为红色。除此之外，一棵红黑树还需要满足这样几个要求:

1. 根节点是黑色的
2. 每个叶子节点都是黑色的空节点（NIL），也就是说，叶子节点不存储数据
    这一步主要是为了简化红黑树的代码实现而设置
3. 任何相邻的节点都不能同时为红色，也就是说，红色节点是被黑色节点隔开的
4. 每个节点，从该节点到达其可达叶子节点的所有路径，都包含相同数目的黑色节点

备注

平衡二叉查找树的初衷，是为了解决二叉查找树因为动态更新导致的性能退化问题。所以，“平衡”的意思可以等价为性能不退化。“近似平衡”就等价为性能不会退化得太严重。

在工程中大家都喜欢用红黑树:

Treap、Splay Tree，绝大部分情况下，它们操作的效率都很高，
    但是也无法避免极端情况下时间复杂度的退化。
    尽管这种情况出现的概率不大，但是对于单次操作时间非常敏感的场景来说，它们并不适用。
AVL 树是一种高度平衡的二叉树，所以查找的效率非常高
    AVL 树为了维持这种高度的平衡，就要付出更多的代价
    每次插入、删除都要做调整，就比较复杂、耗时
    对于有频繁的插入、删除操作的数据集合，使用 AVL 树的代价就有点高了
红黑树只是做到了近似平衡，并不是严格的平衡，
    所以在维护平衡的成本上，要比 AVL 树要低。
    红黑树的插入、删除、查找各种操作性能都比较稳定

备注

红黑树是一种性能非常稳定的二叉查找树，所以，在工程中，但凡是用到动态插入、删除、查找数据的场景，都可以用到它。不过，它实现起来比较复杂，如果自己写代码实现，难度会有些高，这个时候，我们其实更倾向用跳表来替代它。

递归树

备注

借助递归树来分析递归算法的时间复杂度。

备注

把递归过程一层一层的分解过程画成图，它其实就是一棵树。我们给这棵树起一个名字，叫作递归树。

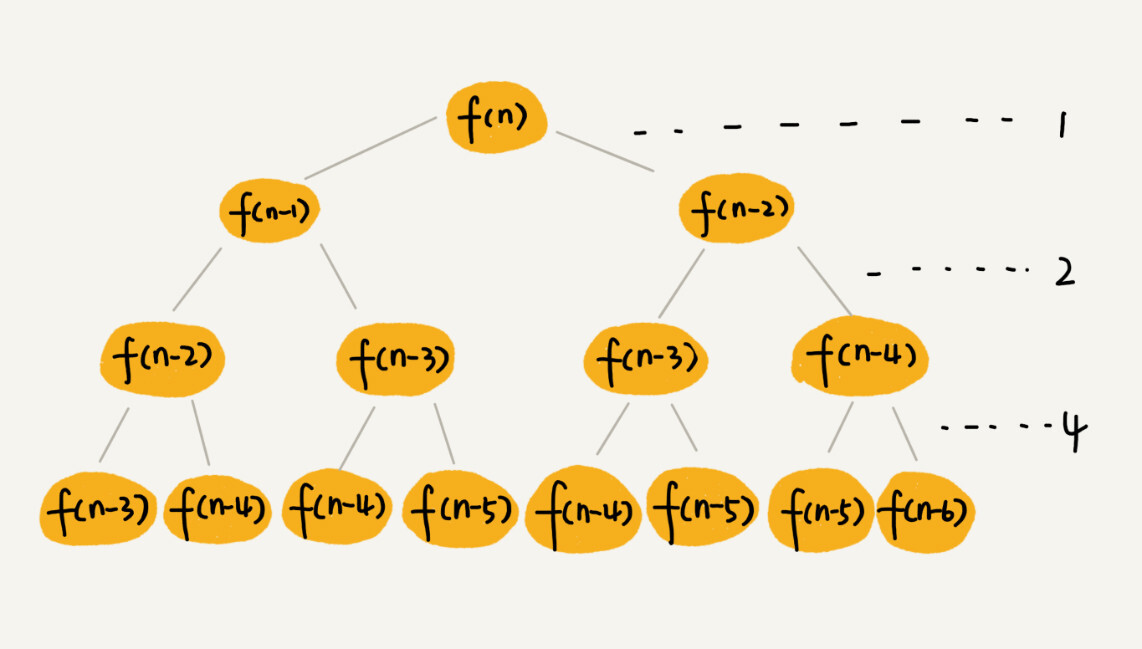
https://img.zhaoweiguo.com/knowledge/images/algorithms/tree2.jpg

一棵斐波那契数列的递归树

这棵递归树的高度是多少:

f(n) 分解为 f(n−1) 和 f(n−2)，每次数据规模都是 −1 或者 −2 叶子节点的数据规模是 1 或者 2 从根节点走到叶子节点，每条路径是长短不一的 1. 最长路径就是最左边这条，每次都是 −1，高度大约就是 n 2. 最短路径就是最右边这条，每次都是 −2，高度大约就是 n/2

每次分解之后的合并操作只需要一次加法运算，时间消耗记作 1
如果路径长度都为 n，那这个总和就是:

1+2+2^2+2^3…+2^(n-1)=2^n-1

如果路径长度都为 n/2，那这个总和就是:

2^(n/2)-1

这个算法的时间复杂度就介于 O(2^n)和O(2^(n/2))之间

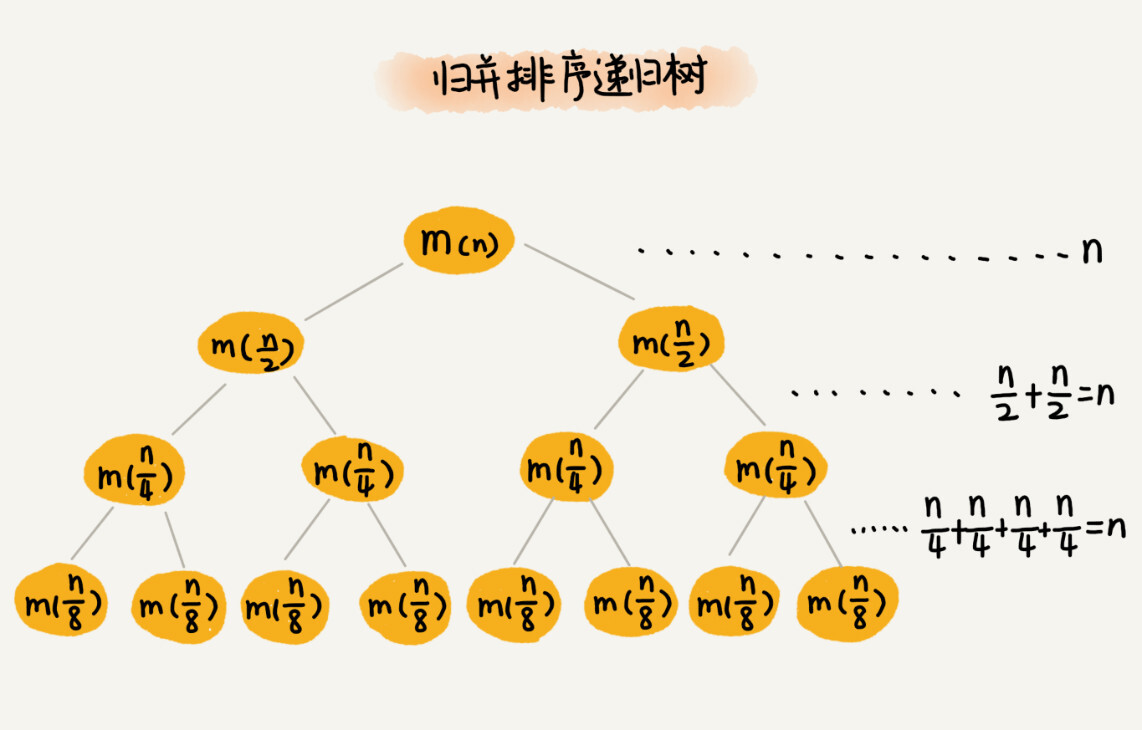
https://img.zhaoweiguo.com/knowledge/images/algorithms/tree3.jpg

每次分解都是一分为二，所以代价很低，我们把时间上的消耗记作常量 1。归并算法中比较耗时的是归并操作，也就是把两个子数组合并为大数组。从图中我们可以看出，每一层归并操作消耗的时间总和是一样的，跟要排序的数据规模有关。我们把每一层归并操作消耗的时间记作 n。 从归并排序的原理和递归树，可以看出来，归并排序递归树是一棵满二叉树。我们前两节中讲到，满二叉树的高度大约是 log2n，所以，归并排序递归实现的时间复杂度就是 O(nlogn)。

备注

两种递归代码的时间复杂度分析方法：有些代码比较适合用递推公式来分析，比如归并排序的时间复杂度、快速排序的最好情况时间复杂度；有些比较适合采用递归树来分析，比如快速排序的平均时间复杂度。而有些可能两个都不怎么适合使用，比如二叉树的递归前中后序遍历。

1 个细胞的生命周期是 3 小时，1 小时分裂一次。求 n 小时后，容器内有多少细胞:

if n==0 f(n)=1
if n==1 f(n)=2
if n==2 f(n)=4
if n==3 f(n)=7
if n>=4 f(n) = f(n-1)*2 - (f(n-3)-f(n-4))

堆和堆排序

堆的定义:

堆是一个完全二叉树
堆中每一个节点的值都必须大于等于（或小于等于）其子树中每个节点的值

大顶堆、小顶堆
堆化: heapify

建堆过程的时间复杂度是 O(n)
排序过程的时间复杂度是 O(nlogn)
所以，堆排序整体的时间复杂度是 O(nlogn)
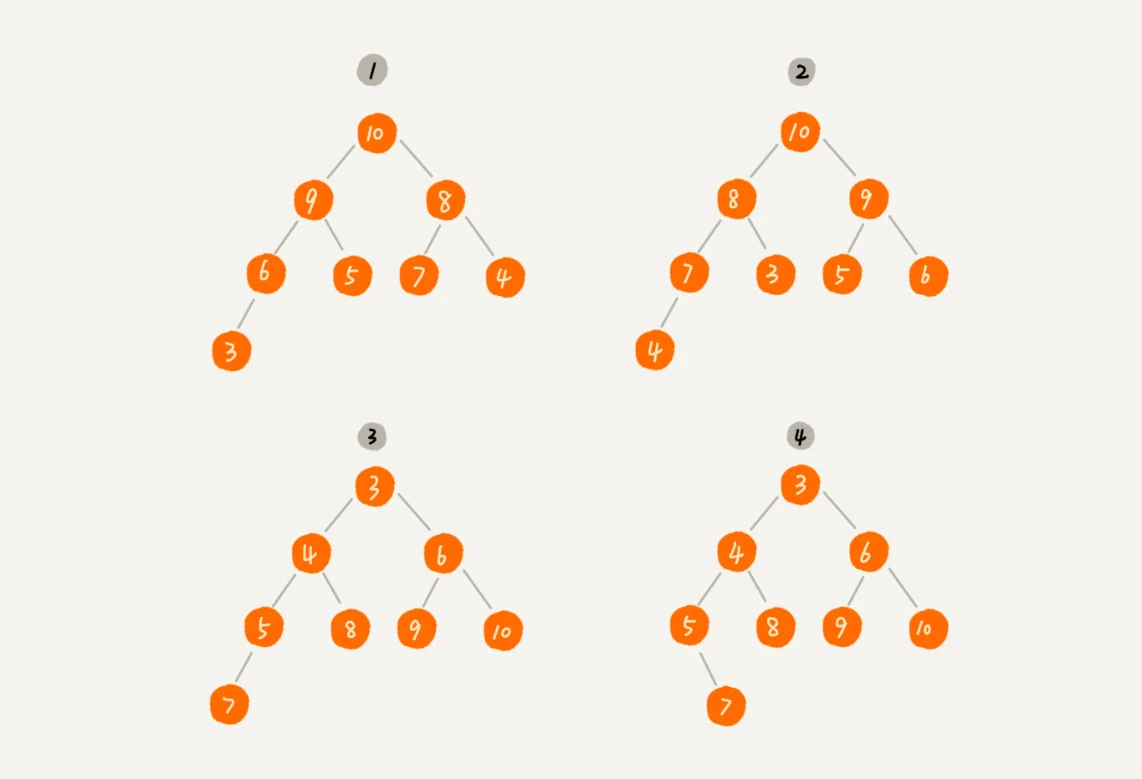
https://img.zhaoweiguo.com/knowledge/images/algorithms/heap1.webp

其中第 1 个和第 2 个是大顶堆，第 3 个是小顶堆，第 4 个不是堆。除此之外，从图中还可以看出来，对于同一组数据，我们可以构建多种不同形态的堆。

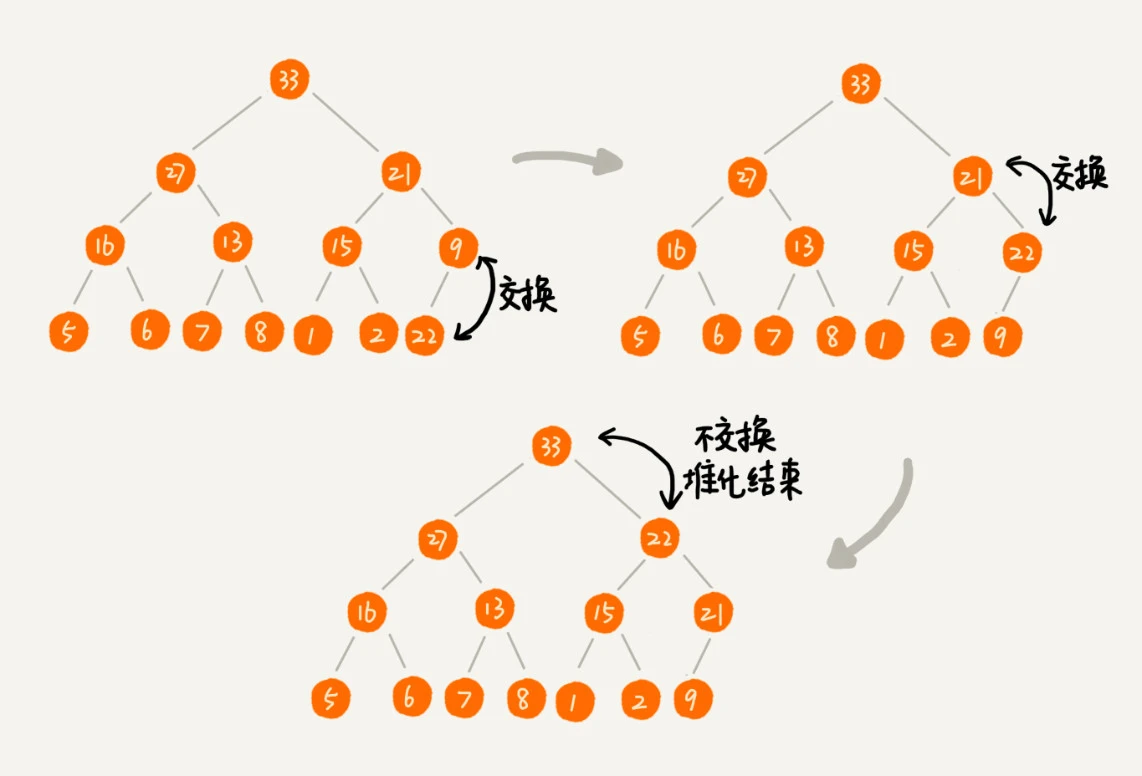
https://img.zhaoweiguo.com/knowledge/images/algorithms/heapify1.webp

1.往堆中插入一个元素: 堆化非常简单，就是顺着节点所在的路径，向上或者向下，对比，然后交换。

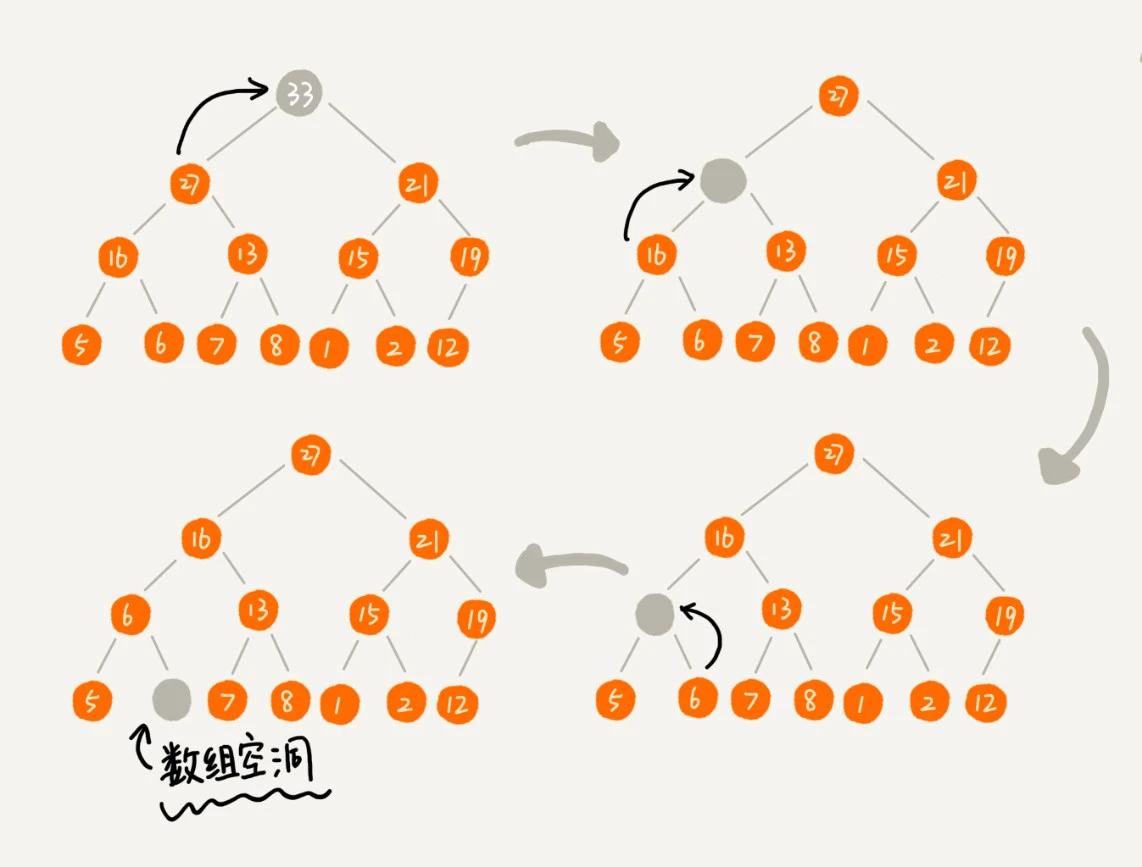
https://img.zhaoweiguo.com/knowledge/images/algorithms/heapify2.webp

2.删除堆顶元素: 按上面的方法有点问题，就是最后堆化出来的堆并不满足完全二叉树的特性。

https://img.zhaoweiguo.com/knowledge/images/algorithms/heapify3.png

2.删除堆顶元素: 稍微改变一下思路，把最后一个节点放到堆顶，然后利用同样的父子节点对比方法。这就是从上往下的堆化方法。因为我们移除的是数组中的最后一个元素，而在堆化的过程中，都是交换操作，不会出现数组中的“空洞”，所以这种方法堆化之后的结果，肯定满足完全二叉树的特性。

备注

堆化的时间复杂度跟树的高度成正比，也就是 O(logn)。插入数据和删除堆顶元素的主要逻辑就是堆化，所以，往堆中插入一个元素和删除堆顶元素的时间复杂度都是 O(logn)。

备注

借助于堆这种数据结构实现的排序算法，就叫做堆排序。这种排序方法的时间复杂度非常稳定，是 O(nlogn)，并且它还是原地排序算法。

堆排序

堆排序的过程大致分解成两个大的步骤:

1. 建堆
2. 排序

  1. 建堆:

    a. 在堆中插入一个元素的思路
    尽管数组中包含 n 个数据，但是我们可以假设，起初堆中只包含一个数据，就是下标为 1 的数据。
    然后，我们调用前面讲的插入操作，将下标从 2 到 n 的数据依次插入到堆中。
    这样我们就将包含 n 个数据的数组，组织成了堆。
b. 从后往前处理数组，并且每个数据都是从上往下堆化
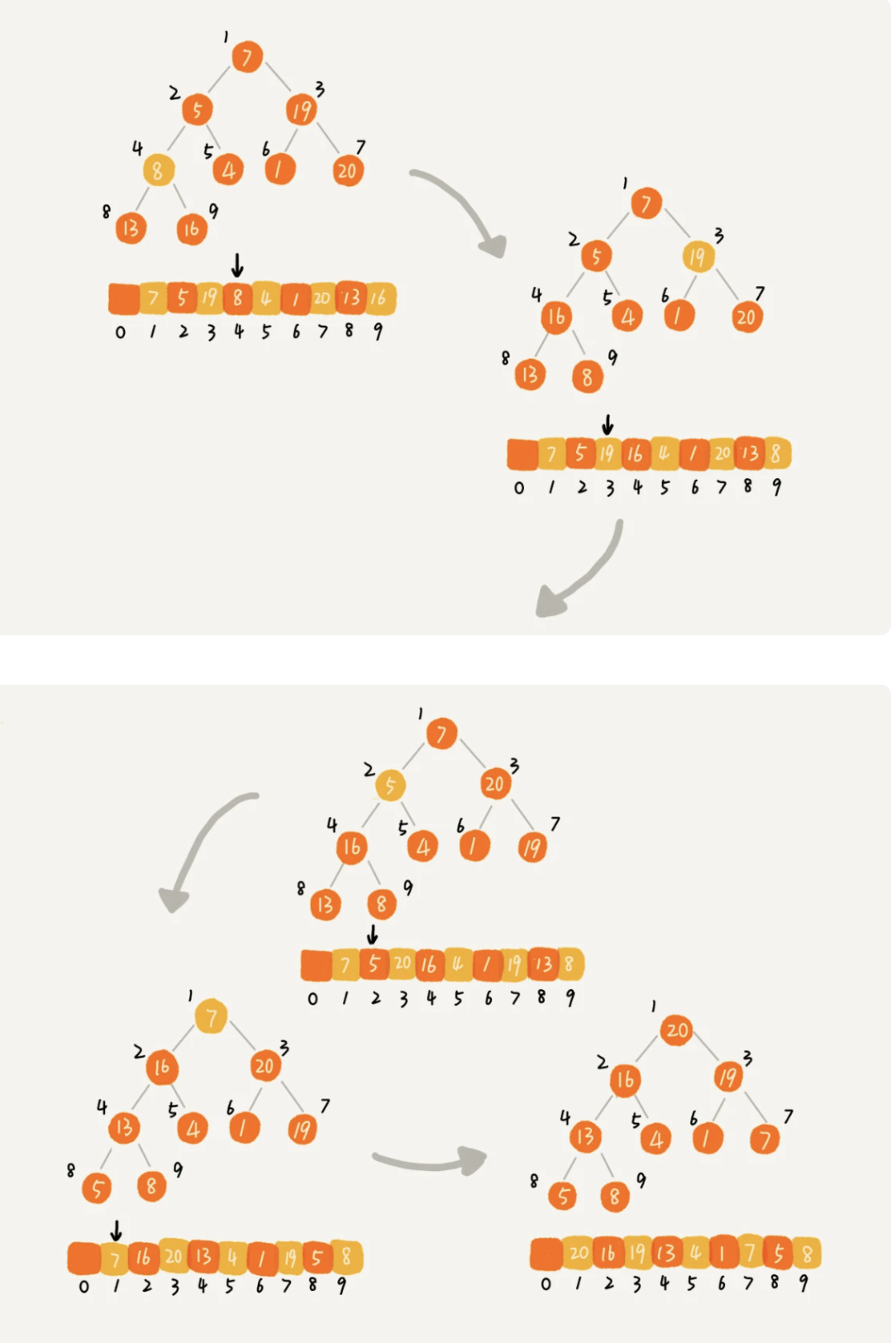
https://img.zhaoweiguo.com/knowledge/images/algorithms/heapify3.png

从上往下堆化分解步骤图

  1. 排序:

    这个过程有点类似上面讲的“删除堆顶元素”的操作，
当堆顶元素移除之后，我们把下标为 n 的元素放到堆顶，
然后再通过堆化的方法，将剩下的 n−1 个元素重新构建成堆
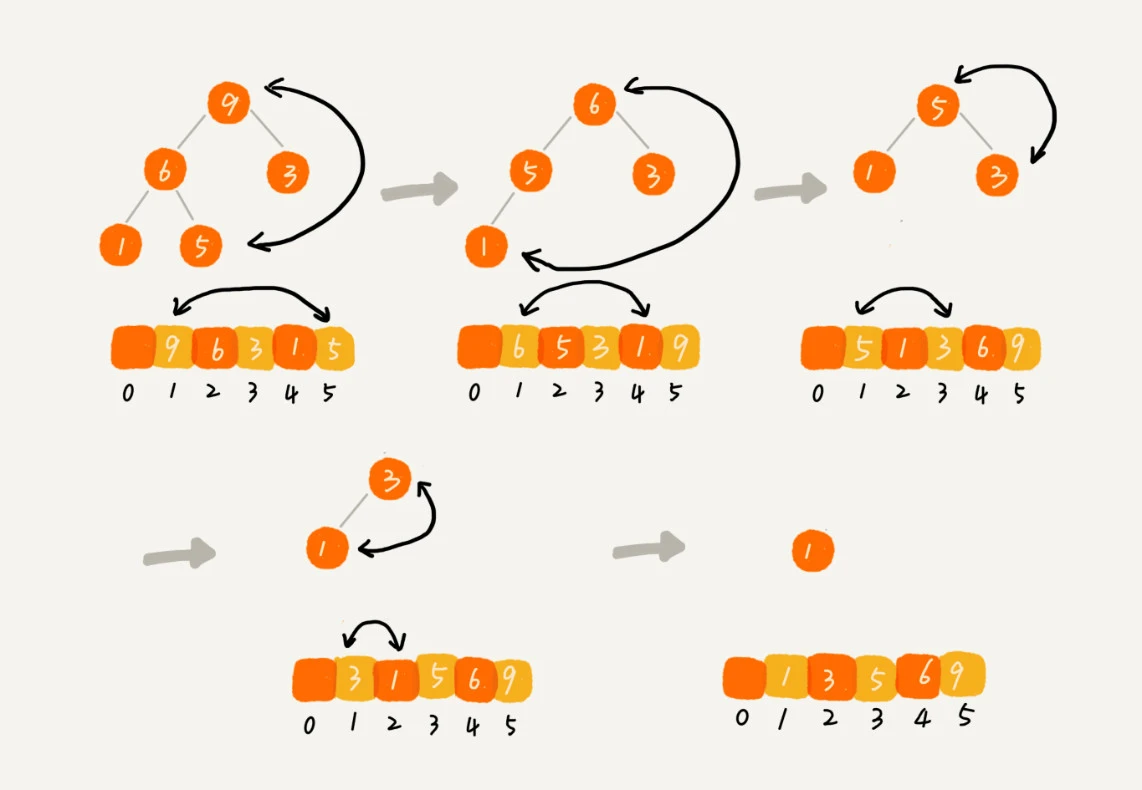
https://img.zhaoweiguo.com/knowledge/images/algorithms/heapify4.webp

堆排序的过程分解步骤图

为什么快速排序要比堆排序性能好:

1. 堆排序数据访问的方式没有快速排序友好
    对于快速排序来说，数据是顺序访问的。而对于堆排序来说，数据是跳着访问的
    这样对 CPU 缓存是不友好的
2. 对于同样的数据，在排序过程中，堆排序算法的数据交换次数要多于快速排序。

堆的应用-优先队列

  • Java 的 PriorityQueue，C++ 的 priority_queue

  • 赫夫曼编码、图的最短路径、最小生成树算法

堆和优先级队列非常相似:

一个堆就可以看作一个优先级队列。只是概念上的区分而已。
往优先级队列中插入一个元素，就相当于往堆中插入一个元素；
从优先级队列中取出优先级最高的元素，就相当于取出堆顶元素。

  1. [实战]合并有序小文件:

    假设我们有 100 个小文件，每个文件的大小是 100MB，每个文件中存储的都是有序的字符串。
我们希望将这些 100 个小文件合并成一个有序的大文件

从这 100 个文件中，各取第一个字符串，放入数组中，
然后比较大小，把最小的那个字符串放入合并后的大文件中，并从数组中删除。

用数组这种数据结构，来存储从小文件中取出来的字符串。
每次从数组中取最小字符串，都需要循环遍历整个数组(数组大小是100)

可以用到优先级队列，也可以说是堆:
    将从小文件中取出来的字符串放入到小顶堆中，
    那堆顶的元素，也就是优先级队列队首的元素，就是最小的字符串。
    我们将这个字符串放入到大文件中，并将其从堆中删除。
    然后再从小文件中取出下一个字符串，放入到堆中。

  2. 高性能定时器:

    定时器中维护了很多定时任务，每个任务都设定了一个要触发执行的时间点。
每过一个很小的单位时间（比如 1 秒），就扫描一遍任务，看是否有任务到达设定的执行时间
每过 1 秒就扫描一遍任务列表的做法比较低效

用优先级队列来解决:
    按照任务设定的执行时间，将这些任务存储在优先级队列中，
    队列首部（也就是小顶堆的堆顶）存储的是最先执行的任务
    a. 只需要看堆顶
    b. 如果没有新任务,可以不用每次检查是否有任务，可以在堆顶任务需要执行时再检查

堆的应用-利用堆求 Top K

求 Top K 的问题抽象成两类:

一类是针对静态数据集合，也就是说数据集合事先确定，不会再变
另一类是针对动态数据集合，也就是说数据集合事先并不确定，有数据动态地加入到集合中

针对静态数据:

维护一个大小为 K 的小顶堆

顺序遍历数组，从数组中取出数据与堆顶元素比较:
    如果比堆顶元素大，我们就把堆顶元素删除，并且将这个元素插入到堆中
    如果比堆顶元素小，则不做处理，继续遍历数组
    等数组中的数据都遍历完之后，堆中的数据就是前 K 大数据了

时间复杂度:
    遍历数组需要 O(n) 的时间复杂度
    一次堆化操作需要 O(logK) 的时间复杂度，
    所以最坏情况下，n 个元素都入堆一次，时间复杂度就是 O(nlogK)

针对动态数据:

同「静态数据」一样先做全量操作
对增量操作:
    一直都维护一个 K 大小的小顶堆
    当有数据被添加到集合中时，也要与堆进行比较判断

堆的应用-利用堆求中位数

对于一组静态数据，中位数是固定的，我们可以先排序，第 n/2 个数据就是中位数。但是，如果我们面对的是动态数据集合，中位数在不停地变动，如果再用先排序的方法，每次询问中位数的时候，都要先进行排序，那效率就不高了。

借助堆这种数据结构实现求中位数操作:

维护两个堆，一个大顶堆，一个小顶堆
    大顶堆、小顶堆各存储一半数据
    小顶堆中的数据都大于大顶堆中的数据。
新添加一个数据时:
    如果新加入的数据小于等于大顶堆的堆顶元素，我们就将这个新数据插入到大顶堆；
    否则，我们就将这个新数据插入到小顶堆
两个堆中的数据个数不符合各一半时:
    从一个堆将堆顶元素移动到另一个堆

时间复杂度:

插入数据因为需要涉及堆化，所以时间复杂度变成了 O(logn)，
但是求中位数我们只需要返回大顶堆的堆顶元素就可以了，所以时间复杂度就是 O(1)

备注

利用两个堆不仅可以快速求出中位数，还可以快速求其他百分位的数据，原理是类似的。如:如何快速求接口的 99% 响应时间？

图

涉及图的算法:

图的搜索
最短路径
最小生成树
二分图

顶点（vertex）
边（edge）
无向图
    顶点的度（degree）
有向图
    入度（In-degree）: 有多少条边指向这个顶点
    出度（Out-degree）: 有多少条边是以这个顶点为起点指向其他顶点
带权图（weighted graph）
    权重（weight）

邻接矩阵-Adjacency Matrix

邻接矩阵-Adjacency Matrix:

对于无向图来说:
    如果顶点 i 与顶点 j 之间有边，我们就将 A[i][j]和 A[j][i]标记为 1
对于有向图来说:
    如果顶点 i 到顶点 j 之间，有一条箭头从顶点 i 指向顶点 j 的边，
    那我们就将 A[i][j]标记为 1
对于带权图:
    数组中就存储相应的权重
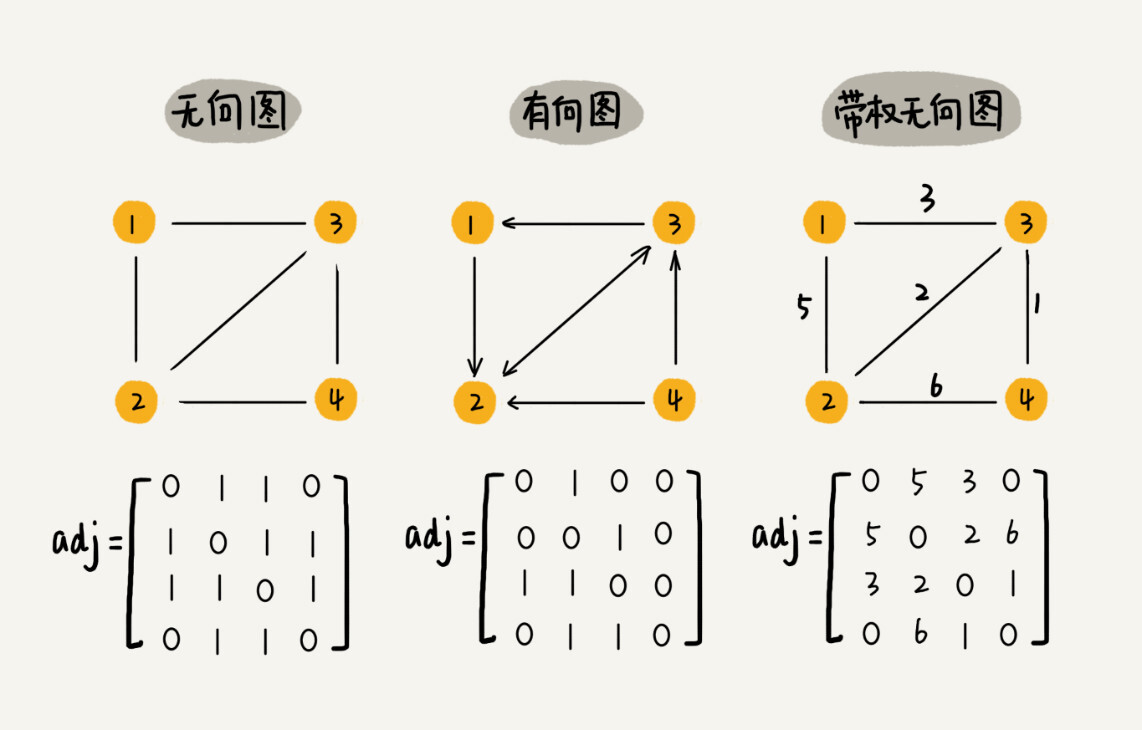
https://img.zhaoweiguo.com/knowledge/images/algorithms/graph1.jpg

备注

用邻接矩阵来表示一个图，虽然简单、直观，但是比较浪费存储空间

邻接矩阵缺点:

比较浪费存储空间
特别对稀疏图-Sparse Matrix:
    顶点很多，但每个顶点的边并不多，那邻接矩阵的存储方法就更加浪费空间
    比如微信有好几亿的用户，对应到图上就是好几亿的顶点
    但每个用户的好友并不会很多，一般也就三五百个而已

邻接矩阵优点:

1. 邻接矩阵的存储方式简单、直接
    因为基于数组，所以在获取两个顶点的关系时，就非常高效
2. 方便计算
    用邻接矩阵的方式存储图，可以将很多图的运算转换成矩阵之间的运算。
    比如求解最短路径问题时有个Floyd-Warshall 算法，利用矩阵循环相乘若干次得到结果

邻接表-Adjacency List

https://img.zhaoweiguo.com/knowledge/images/algorithms/graph1.jpg

备注

邻接表存储起来比较节省空间，但是使用起来就比较耗时间。

图-搜索算法

备注

大部分涉及搜索的场景都可以抽象成“图”

深度优先、广度优先搜索
A*、IDA* 等启发式搜索算法。

广度优先搜索-BFS

  • BFS: Breadth-First-Search(广度优先搜索)

深度优先搜索-DFS

  • 深度优先搜索（Depth-First-Search），简称 DFS

  • 迷宫存储问题

  • 欧拉七桥问题

字符串匹配算法

单模式串匹配的算法: 一个模式串和一个主串之间进行匹配
    BF 算法和 RK 算法
    BM 算法和 KMP 算法
多模式串匹配算法: 在多个模式串和一个主串之间做匹配
    Trie 树和 AC 自动机

BF 算法

  • Brute Force

  • 暴力匹配算法，也叫朴素匹配算法

备注

主串的长度记作 n，模式串的长度记作 m。在主串中，检查起始位置分别是 0、1、2….n-m 且长度为 m 的 n-m+1 个子串，看有没有跟模式串匹配的

复杂度:

最坏情况时间复杂度是 O(n*m)

时间复杂度很高但还是较常用的字符串匹配算法原因:

1. 实际的软件开发中，大部分情况下，模式串和主串的长度都不会太长
2. 算法思想简单，代码实现也非常简单

RK 算法

  • Rabin-Karp 算法: 两位发明者 Rabin 和 Karp 的名字来命名

备注

借助哈希算法来实现高效字符串匹配。

RK 算法的思路是这样的:

通过哈希算法对主串中的 n-m+1 个子串分别求哈希值，
然后逐个与模式串的哈希值比较大小
如果某个子串的哈希值与模式串相等，那就说明对应的子串和模式串匹配了
（这里先不考虑哈希冲突的问题，后面我们会讲到）
因为哈希值是一个数字，数字之间比较是否相等是非常快速的，所以模式串和子串比较的效率就提高了。

备注

【小技巧】假设要匹配的字符串的字符集中只包含 K 个字符，我们可以用一个 K 进制数来表示一个子串，这个 K 进制数转化成十进制数，作为子串的哈希值。

备注

比如要处理的字符串只包含 a～z 这 26 个小写字母，那我们就用二十六进制来表示一个字符串。我们把 a～z 这 26 个字符映射到 0～25 这 26 个数字，a 就表示 0，b 就表示 1，以此类推，z 表示 25。

https://img.zhaoweiguo.com/knowledge/images/algorithms/string-match1.jpg

【小技巧】事先计算好 26^0、26^1、26^2……26^(m-1)，并且存储在一个长度为 m 的数组中，公式中的“次方”就对应数组的下标。当我们需要计算 26 的 x 次方的时候，就可以从数组的下标为 x 的位置取值，直接使用，省去了计算的时间。

时间复杂度:

RK 算法包含两部分:
1. 计算子串哈希值
    只需要扫描一遍主串就能计算出所有子串的哈希值了，所以这部分的时间复杂度是 O(n)
2. 模式串哈希值与子串哈希值之间的比较
    模式串哈希值与每个子串哈希值之间的比较的时间复杂度是 O(1)，
    总共需要比较 n-m+1 个子串的哈希值，所以，这部分的时间复杂度也是 O(n)

备注

上面设计的哈希算法是没有散列冲突的。但还有一个问题就是，模式串很长，相应的主串中的子串也会很长，通过上面的哈希算法计算得到的哈希值就可能很大，如果超过了计算机中整型数据可以表示的范围

哈希算法的其他设计方法:

1. 把字符串中每个字母对应的数字相加
    假设字符串中只包含 a～z 这 26 个英文字母，
    那我们每个字母对应一个数字，比如 a 对应 1，b 对应 2，以此类推，z 对应 26。
    我们可以把字符串中每个字母对应的数字相加，最后得到的和作为哈希值
    这种哈希算法的哈希冲突概率也是挺高的
2. 每一个字母从小到大对应一个素数:
    而不是 1，2，3……这样的自然数，
    这样冲突的概率就会降低一些

哈希算法的冲突解决:

当我们发现一个子串的哈希值跟模式串的哈希值相等的时候，
我们只需要再对比一下子串和模式串本身就好了

BM 算法

  • BM（Boyer-Moore）算法

性能是著名的 KMP 算法的 3 到 4 倍
BM 算法的原理很复杂，比较难懂，学起来会比较烧脑

BM 算法包含两部分:

1. 坏字符规则（bad character rule）
2. 好后缀规则（good suffix shift）

KMP 算法

  • KMP 算法是根据三位作者（D.E.Knuth，J.H.Morris 和 V.R.Pratt）的名字来命名的

  • 全称是 Knuth Morris Pratt 算法

KMP 算法的核心思想:

假设主串是 a，模式串是 b。
在模式串与主串匹配的过程中，当遇到不可匹配的字符的时候，我们希望找到一些规律，
可以将模式串往后多滑动几位，跳过那些肯定不会匹配的情况。

坏字符
好前缀

Trie 树

  • Trie 树，也叫“字典树”

备注

Trie 树的本质，就是利用字符串之间的公共前缀，将重复的前缀合并在一起

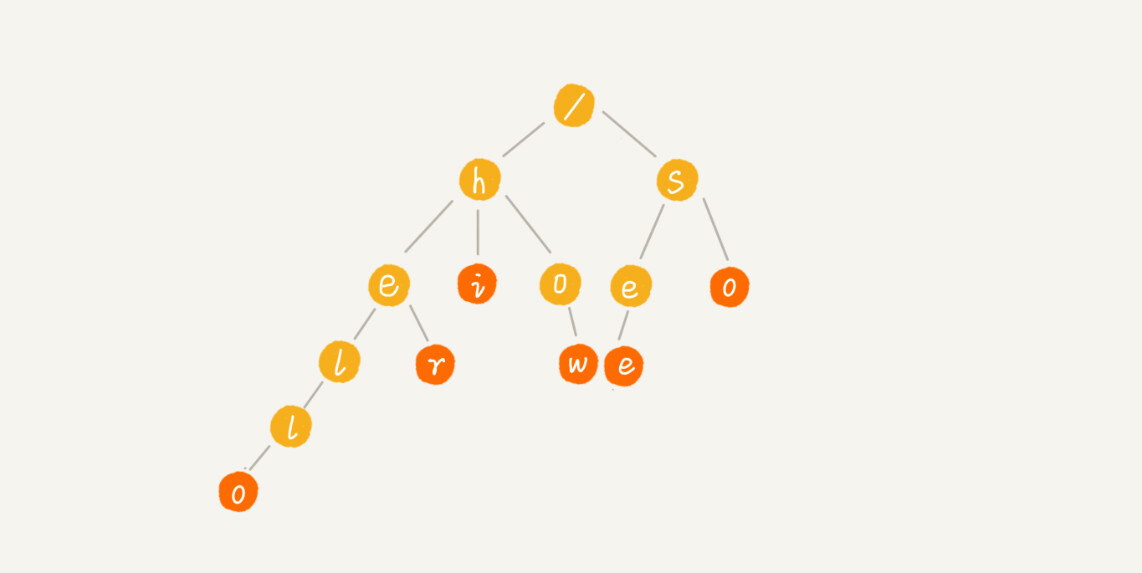
https://img.zhaoweiguo.com/knowledge/images/algorithms/tree-trie1.jpg

Trie 树主要有两个操作:

1. 将字符串集合构造成 Trie 树
    这个过程分解开来的话，就是一个将字符串插入到 Trie 树的过程
2. 在 Trie 树中查询一个字符串

时间复杂度:

构建 Trie 树的过程，需要扫描所有的字符串，
    时间复杂度是 O(n)（n 表示所有字符串的长度和）
查找字符串的时间复杂度是 O(k)，k 表示要查找的字符串的长度
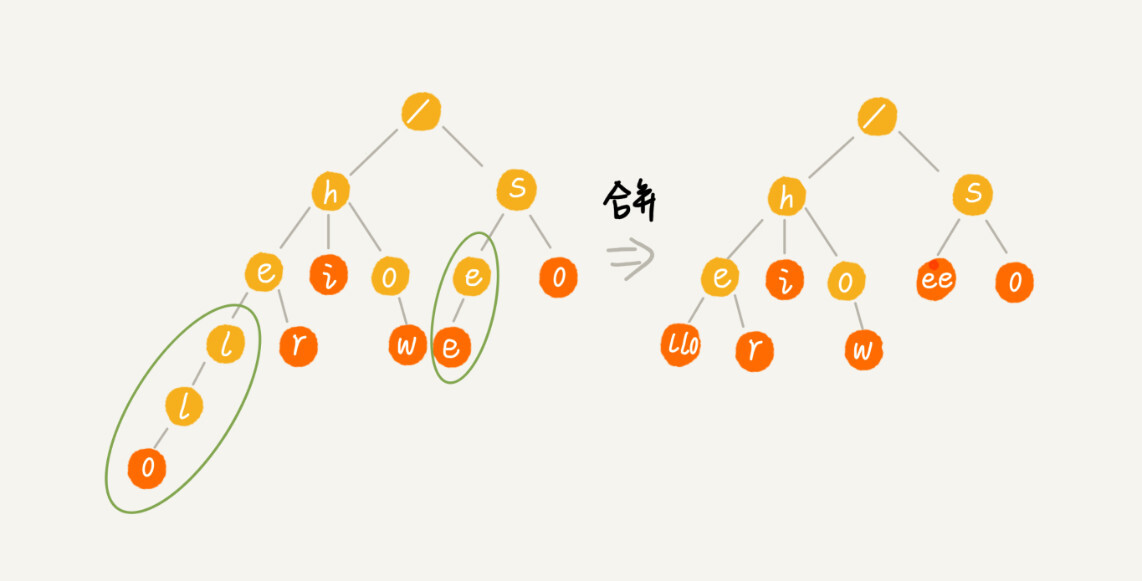
https://img.zhaoweiguo.com/knowledge/images/algorithms/tree-trie2.jpg

Trie 树的变体有很多，都可以在一定程度上解决内存消耗的问题。比如，缩点优化，就是对只有一个子节点的节点，而且此节点不是一个串的结束节点，可以将此节点与子节点合并。

Trie 树适合的场景:

1. 字符串中包含的字符集不能太大
    如果字符集太大，那存储空间可能就会浪费很多。
    即便可以优化，但也要付出牺牲查询、插入效率的代价。
2. 字符串的前缀重合比较多
3. 指针串起来的数据块是不连续的
    Trie 树中用到了指针，所以，对缓存并不友好，性能上会打个折扣。

场景举例:

1. 搜索引擎的搜索关键词提示功能
2. 自动输入补全，比如:
    输入法自动补全功能、IDE 代码编辑器自动补全功能、浏览器网址输入的自动补全功能

更多思考:

DAT（双数组trie树）
后缀树

AC自动机

  • AC 自动机算法，全称是 Aho-Corasick 算法

  • AC 自动机是基于 Trie 树的一种改进算法

  • Trie 树跟 AC 自动机之间的关系，就像单串匹配中朴素的串匹配算法，跟 KMP 算法之间的关系一样

备注

AC 自动机实际上就是在 Trie 树之上，加了类似 KMP 的 next 数组，只不过此处的 next 数组是构建在树上罢了

AC 自动机算法包含两个部分:

1. 将多个模式串构建成 AC 自动机
    a. 将模式串构建成 Trie 树
    b. 在 Trie 树上构建失败指针
2. 在 AC 自动机中匹配主串

各类数据结构对比

散列表：插入删除查找都是O(1), 是最常用的，但其缺点是不能顺序遍历以及扩容缩容的性能损耗。适用于那些不需要顺序遍历，数据更新不那么频繁的。

跳表：插入删除查找都是O(logn), 并且能顺序遍历。缺点是空间复杂度O(n)。适用于不那么在意内存空间的，其顺序遍历和区间查找非常方便。

红黑树：插入删除查找都是O(logn), 中序遍历即是顺序遍历，稳定。缺点是难以实现，去查找不方便。其实跳表更佳，但红黑树已经用于很多地方了。

贪心算法-greedy algorithm

经典的应用:

霍夫曼编码（Huffman Coding）
Prim 和 Kruskal 最小生成树算法
Dijkstra 单源最短路径算法

贪心算法解决问题的步骤:

1. 定义了限制值和期望值: 希望从中选出几个数据，在满足限制值的情况下，期望值最大
2. 每次选择: 在当前情况下，在对限制值同等贡献量的情况下，对期望值贡献最大的数据
3. 从实践的角度来说，大部分能用贪心算法解决的问题
    贪心算法的正确性都是显而易见的，也不需要严格的数学推导证明

有权图中，我们从顶点 S 开始，找一条到顶点 T 的最短路径:

用贪心的选择方式，最终求的路径并不是最短路径
主要原因是:
    前面的选择，会影响后面的选择。
    即便我们第一步选择最优的走法（边最短），
    但可能因为这一步选择，导致后面每一步的选择都很糟糕，最终也就无缘全局最优解

  1. 实例-分糖果:

    有 m 个糖果和 n 个孩子。我们现在要把糖果分给这些孩子吃
但是糖果少，孩子多（m<n），所以糖果只能分配给一部分孩子
每个糖果的大小不等，这 m 个糖果的大小分别是 s1，s2，s3，……，sm
每个孩子对糖果大小的需求也不一样: 分别是 g1，g2，g3，……，gn
只有糖果的大小大于等于孩子的对糖果大小的需求的时候，孩子才得到满足

提问: 如何分配糖果，能尽可能满足最多数量的孩子？

  2. 实例-钱币找零:

    假设我们有 1 元、2 元、5 元、10 元、20 元、50 元、100 元这些面额的纸币，
它们的张数分别是 c1、c2、c5、c10、c20、c50、c100。

提问: 现在要用这些钱来支付 K 元，最少要用多少张纸币呢

  3. 实例-区间覆盖:

    假设我们有 n 个区间，
区间的起始端点和结束端点分别是[l1, r1]，[l2, r2]，[l3, r3]，……，[ln, rn]
我们从这 n 个区间中选出一部分区间，这部分区间满足两两不相交（端点相交的情况不算相交）

提问: 最多能选出多少个区间呢

这个处理思想在很多贪心算法问题中都有用到，比如任务调度、教师排课等

解决思路:
    我们假设这 n 个区间中最左端点是 lmin，最右端点是 rmax
    这个问题就相当于，我们选择几个不相交的区间，从左到右将[lmin, rmax]覆盖上
    我们按照起始端点从小到大的顺序对这 n 个区间排序

每次选择的时候:
    左端点跟前面的已经覆盖的区间不重合的，右端点又尽量小的，
    这样可以让剩下的未覆盖区间尽可能的大，就可以放置更多的区间

霍夫曼编码

用贪心算法实现霍夫曼编码:

霍夫曼编码是十分有效的编码方法，广泛用于数据压缩中，其压缩率在 20%～90% 之间
不仅会考察文本中有多少个不同字符，还考察每个字符出现的频率，根据频率的不同，选择不同长度的编码

备注

假设我有一个包含 1000 个字符的文件，每个字符占 1 个 byte（1byte=8bits），存储这 1000 个字符就一共需要 8000bits，那有没有更加节省空间的存储方式呢？

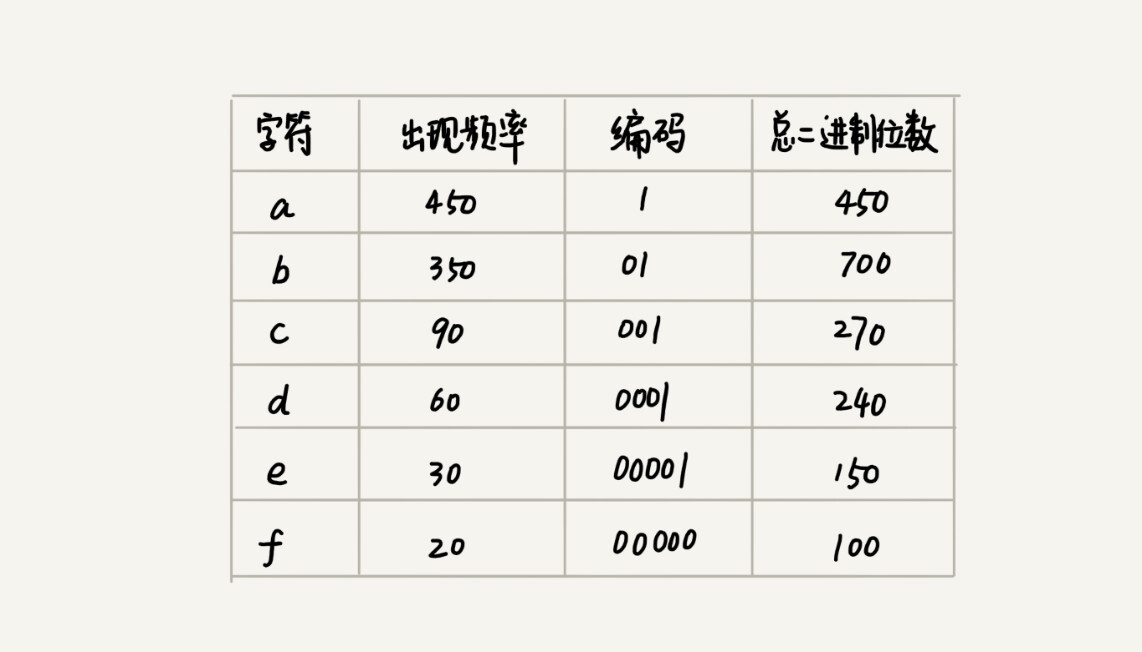
https://img.zhaoweiguo.com/knowledge/images/algorithms/huffman1.jpg

假设这 6 个字符出现的频率从高到低依次是 a、b、c、d、e、f。看本图的「编码」列，任何一个字符的编码都不是另一个的前缀，在解压缩的时候，我们每次会读取尽可能长的可解压的二进制串，所以在解压缩的时候也不会歧义。经过这种编码压缩之后，这 1000 个字符只需要 2100bits 就可以了

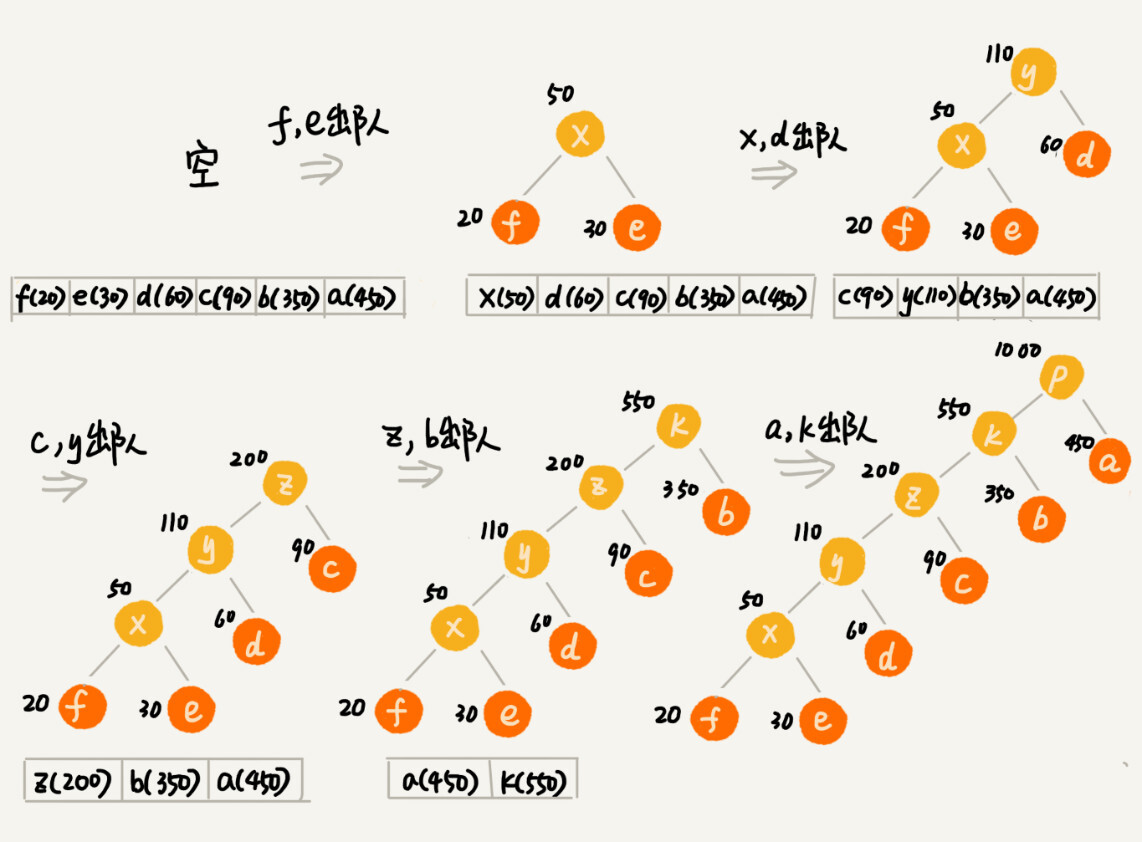
https://img.zhaoweiguo.com/knowledge/images/algorithms/huffman2.jpg

把每个字符看作一个节点，并且附带着把频率放到优先级队列中。我们从队列中取出频率最小的两个节点 A、B，然后新建一个节点 C，把频率设置为两个节点的频率之和，并把这个新节点 C 作为节点 A、B 的父节点。最后再把 C 节点放入到优先级队列中。重复这个过程，直到队列中没有数据。

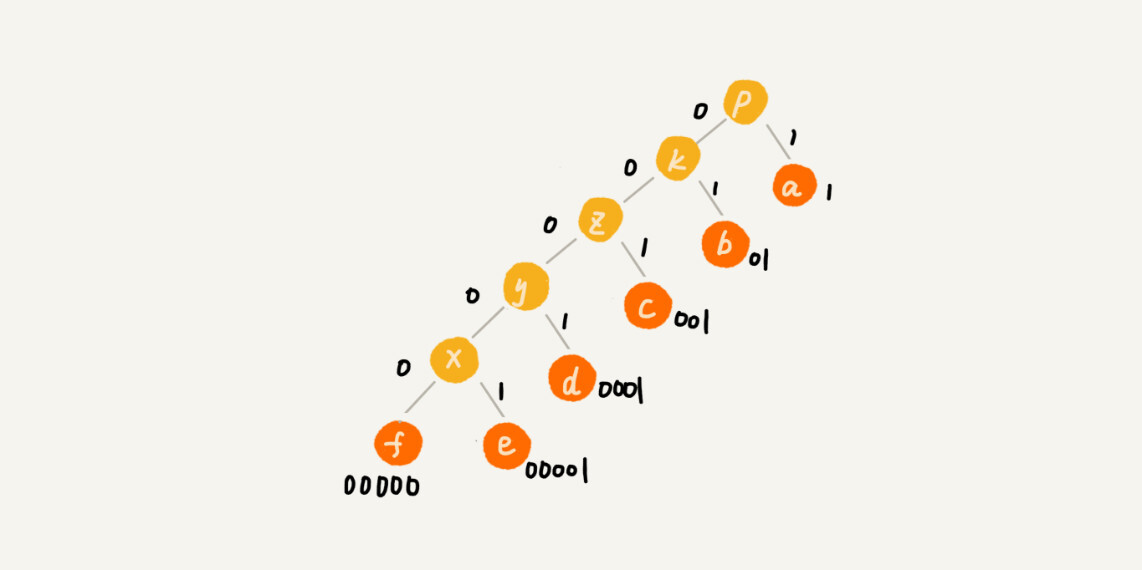
https://img.zhaoweiguo.com/knowledge/images/algorithms/huffman3.jpg

我们给每一条边加上画一个权值，指向左子节点的边我们统统标记为 0，指向右子节点的边，我们统统标记为 1，那从根节点到叶节点的路径就是叶节点对应字符的霍夫曼编码。

备注

贪心算法的最难的一块是如何将要解决的问题抽象成贪心算法模型

分治算法

  • divide and conquer

MapReduce
倒排索引
PageRank 计算
网页分析等搜索引擎相关的技术

核心思想:

本质就是四个字，分而治之
也就是将原问题划分成 n 个规模较小，并且结构与原问题相似的子问题，
递归地解决这些子问题，然后再合并其结果，就得到原问题的解。

备注

分治算法是一种处理问题的思想，递归是一种编程技巧

分治算法能解决的问题，一般需要满足下面这几个条件:

1. 原问题与分解成的小问题具有相同的模式
2. 原问题分解成的子问题可以独立求解，子问题之间没有相关性
    这一点是分治算法跟动态规划的明显区别
3. 具有分解终止条件，也就是说，当问题足够小时，可以直接求解
4. 可以将子问题合并成原问题，而这个合并操作的复杂度不能太高
    否则就起不到减小算法总体复杂度的效果了

  • leetcode 315

回溯算法

应用:

深度优先搜索算法
正则表达式匹配
编译原理中的语法分析

经典的数学问题:

数独
八皇后
0-1 背包
图的着色
旅行商问题
全排列

备注

回溯算法非常适合用递归来实现，在实现的过程中，剪枝操作是提高回溯效率的一种技巧。利用剪枝，我们并不需要穷举搜索所有的情况，从而提高搜索效率。本质就是『暴力枚举』

动态规划-Dynamic Programming

备注

动态规划比较适合用来求解最优问题，比如求最大值、最小值等等。它可以非常显著地降低时间复杂度，提高代码的执行效率。不过，它也是出了名的难学。

备注

[动态规划名字的由来]我们把问题分解为多个阶段，每个阶段对应一个决策。我们记录每一个阶段可达的状态集合（去掉重复的），然后通过当前阶段的状态集合，来推导下一个阶段的状态集合，动态地往前推进。

备注

大部分动态规划能解决的问题，都可以通过回溯算法来解决，只不过回溯算法解决起来效率比较低，时间复杂度是指数级的。动态规划算法，在执行效率方面，要高很多。尽管执行效率提高了，但是动态规划的空间复杂度也提高了，所以，很多时候，我们会说，动态规划是一种空间换时间的算法思想。

一个模型三个特征:

多阶段决策最优解模型
    解决最优问题的过程，需要经历多个决策阶段。
    每个决策阶段都对应着一组状态。
    然后我们寻找一组决策序列，经过这组决策序列，能够产生最终期望求解的最优值。

1. 最优子结构
    问题的最优解包含子问题的最优解。
    反过来说就是，我们可以通过子问题的最优解，推导出问题的最优解。
    如果我们把最优子结构，对应到我们前面定义的动态规划问题模型上，
    那我们也可以理解为，后面阶段的状态可以通过前面阶段的状态推导出来。
2. 无后效性
    无后效性有两层含义:
    第一层含义是，在推导后面阶段的状态的时候，
        我们只关心前面阶段的状态值，不关心这个状态是怎么一步一步推导出来的。
    第二层含义是，某阶段状态一旦确定，就不受之后阶段的决策影响。
        无后效性是一个非常“宽松”的要求。
        只要满足前面提到的动态规划问题模型，其实基本上都会满足无后效性。
3. 重复子问题
    不同的决策序列，到达某个相同的阶段时，可能会产生重复的状态。

解决动态规划问题的两种思路:

1. 状态转移表法
    步骤:
        - 回溯算法实现: 一般能用动态规划解决的问题，都可以使用回溯算法的暴力搜索解决
        - 定义状态: 每个状态表示一个节点
        - 画递归树: 然后对应画出递归树
        - 找重复子问题: 从递归树中，能看出来，重复子问题是否存在，以及是如何产生的
        - 画状态转移表: 状态表一般是二维的，把它想象成二维数组。每个状态含三个变量，行、列、数组值
        - 根据递推关系填表: 根据决策先后过程，从前往后，根据递推关系，分阶段填充状态表中的每个状态
        - 将填表过程翻译成代码
    找到重复子问题后有两种处理思路:
        a. 直接用 **回溯加“备忘录”** 的方法，来避免重复子问题
        b. 使用 **动态规划的解决方法，状态转移表法**
2. 状态转移方程法
    说明:
        如果问题的状态比较复杂，需要很多变量来表示，那对应的状态表可能就是高维的(三维、四信维)
        不适合用状态转移表法来解决: a. 图不好画 b. 不好理解
    步骤:
        - 找最优子结构: 分析某个问题如何通过子问题来递归求解
        - 写状态转移方程: 根据最优子结构，写出递归公式，也就是所谓的状态转移方程
        - 将状态转移方程翻译成代码
    有两种代码实现方法:
        一种是递归加“备忘录”
        另一种是迭代递推

  • 编辑距离-Edit Distance:

    将一个字符串转化成另一个字符串，需要的最少编辑操作次数（如增加、删除、替换一个字符）
编辑距离越大，说明两个字符串的相似程度越小；
相反，编辑距离就越小，说明两个字符串的相似程度越大。
对于两个完全相同的字符串来说，编辑距离就是 0。

莱文斯坦距离（Levenshtein distance）
    允许增加、删除、替换字符这三个编辑操作
    莱文斯坦距离的大小，表示两个字符串差异的大小
最长公共子串长度（Longest common substring length）
    只允许增加、删除字符这两个编辑操作
    最长公共子串的大小，表示两个字符串相似程度的大小
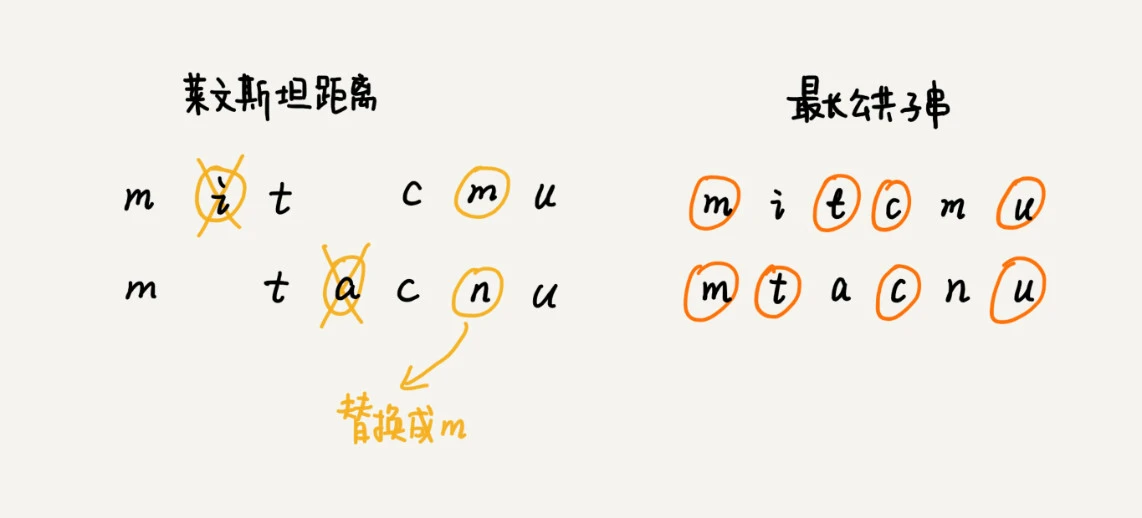
https://img.zhaoweiguo.com/knowledge/images/algorithms/edit-distance1.jpg

两个字符串 mitcmu 和 mtacnu 的莱文斯坦距离是 3，最长公共子串长度是 4

拓扑排序

  • Topologically sort

  • 拓扑排序是一种用于有向无环图（DAG）中的排序算法。

  • 它的目的是将图中的所有节点排成一个线性序列，使得对于每一条有向边 u→v，节点 u 在节点 v 之前出现。

  • 拓扑排序通常用于处理任务调度、课程安排等需要满足某种依赖关系的场景。

拓扑排序有两种实现方法:

1. Kahn 算法
    实际上用的是贪心算法思想，思路非常简单、好懂:
        顶点入度为 0: 没有任何顶点必须先于这个顶点执行
    步骤:
        a. 先从图中，找出一个入度为 0 的顶点，将其输出到拓扑排序的结果序列中
        b. 把这个顶点从图中删除（也就是把这个顶点可达的顶点的入度都减 1）
        c. 循环执行上面的过程，直到所有的顶点都被输出
        最后输出的序列，就是满足局部依赖关系的拓扑排序
    时间复杂度:
        O (V+E)（V 表示顶点个数，E 表示边的个数）
2. DFS 深度优先搜索算法
    深度优先遍历，遍历图中的所有顶点，而非只是搜索一个顶点到另一个顶点的路径
    a. 通过邻接表构造逆邻接表
        邻接表中，边 s->t 表示 s 先于 t 执行，也就是 t 要依赖 s。
        在逆邻接表中，边 s->t 表示 s 依赖于 t，s 后于 t 执行
    b. 算法的核心，也就是递归处理每个顶点
        对于顶点 vertex 来说，我们先输出它可达的所有顶点，
        也就是说，先把它依赖的所有的顶点输出了，然后再输出自己
    时间复杂度也是 O (V+E)

备注

凡是需要通过局部顺序来推导全局顺序的，一般都能用拓扑排序来解决。

除此之外，拓扑排序还能检测图中环的存在:

对于 Kahn 算法来说，如果最后输出出来的顶点个数，少于图中顶点个数，
图中还有入度不是 0 的顶点，那就说明，图中存在环。

环的检测问题并不需要动用复杂的拓扑排序算法:
    而只需要记录已经访问过的用户 ID，当用户 ID 第二次被访问的时候，就说明存在环

示例:

# 简单的有向无环图：
  5 → 0 ← 4
  ↑    ↓
  2    1 → 3
# 这个图的拓扑排序可能是以下几种之一：
  4, 5, 2, 0, 1, 3
  4, 2, 5, 0, 1, 3
  5, 2, 4, 0, 1, 3

关键特点:

有向无环图：拓扑排序只能应用于有向无环图（DAG），即图中不存在任何环路。
线性序列：排序结果是图中所有节点的一个线性排列，满足每个节点的所有前置节点都排在它之前。
依赖关系：拓扑排序确保在满足依赖关系的前提下，尽可能早地安排每个节点。

最短路径算法-Shortest Path Algorithm

  • 针对有权图，也就是图中的每条边都有一个权重

最短路径算法:

Dijkstra 算法
Bellford 算法
Floyd 算法

单源最短路径算法(一个顶点到一个顶点)的Dijkstra 算法的核心逻辑:

我们用 vertexes 数组，记录从起始顶点到每个顶点的距离（dist）。
起初，我们把所有顶点的 dist 都初始化为无穷大（也就是代码中的 Integer.MAX_VALUE）。
我们把起始顶点的 dist 值初始化为 0，然后将其放到优先级队列中。
我们从优先级队列中取出 dist 最小的顶点 minVertex，
然后考察这个顶点可达的所有顶点（代码中的 nextVertex）。
如果 minVertex 的 dist 值加上 minVertex 与 nextVertex 之间边的权重 w 小于 nextVertex 当前的 dist 值，
也就是说，存在另一条更短的路径，它经过 minVertex 到达 nextVertex。
那我们就把 nextVertex 的 dist 更新为 minVertex 的 dist 值加上 w。
然后，我们把 nextVertex 加入到优先级队列中。
重复这个过程，直到找到终止顶点 t 或者队列为空。

时间复杂度就是 O (E*logV)

备注

对于软件开发工程师来说，我们经常要根据问题的实际背景，对解决方案权衡取舍。类似出行路线这种工程上的问题，我们没有必要非得求出个绝对最优解。很多时候，为了兼顾执行效率，我们只需要计算出一个可行的次优解就可以了。

位图-bitmap

  • 布隆过滤器（Bloom Filter）: 基于位图，是对位图的一种改进

  • 布尔类型，一般大小 1 字节的。实际上，表示 true 和 false 两个值，我们只需要用一个二进制位（bit）就可以了

我们有 1 千万个整数，整数的范围在 1 到 1 亿之间。如何快速查找某个整数是否在这 1 千万个整数中呢？如果用散列表存储这 1 千万的数据，数据是 32 位的整型数，也就是需要 4 个字节的存储空间，那总共至少需要 40MB 的存储空间。如果我们通过位图的话，数字范围在 1 到 1 亿之间，只需要 1 亿个二进制位，也就是 12MB 左右的存储空间就够了。

哈希函数会存在冲突的问题，为了降低这种冲突概率，当然我们可以设计一个复杂点:

 K 个哈希函数，对同一个数字进行求哈希值，那会得到 K 个不同的哈希值，
    我们分别记作 X1, X2, ... Xk
我们把这 K 个数字作为位图中的下标，
    将对应的 BitMap[X1],BitMap[X2]...BitMap[Xk]都设置成 true
即用 K 个二进制位，来表示一个数字的存在

要查询某个数字是否存在的时候:
    我们用同样的 K 个哈希函数，对这个数字求哈希值，分别得到 Y1, Y2, ... Yk
    这 K 个哈希值，如果都是 true，则说明，这个数字存在，
    如果有其中任意一个不为 true，那就说明这个数字不存在。
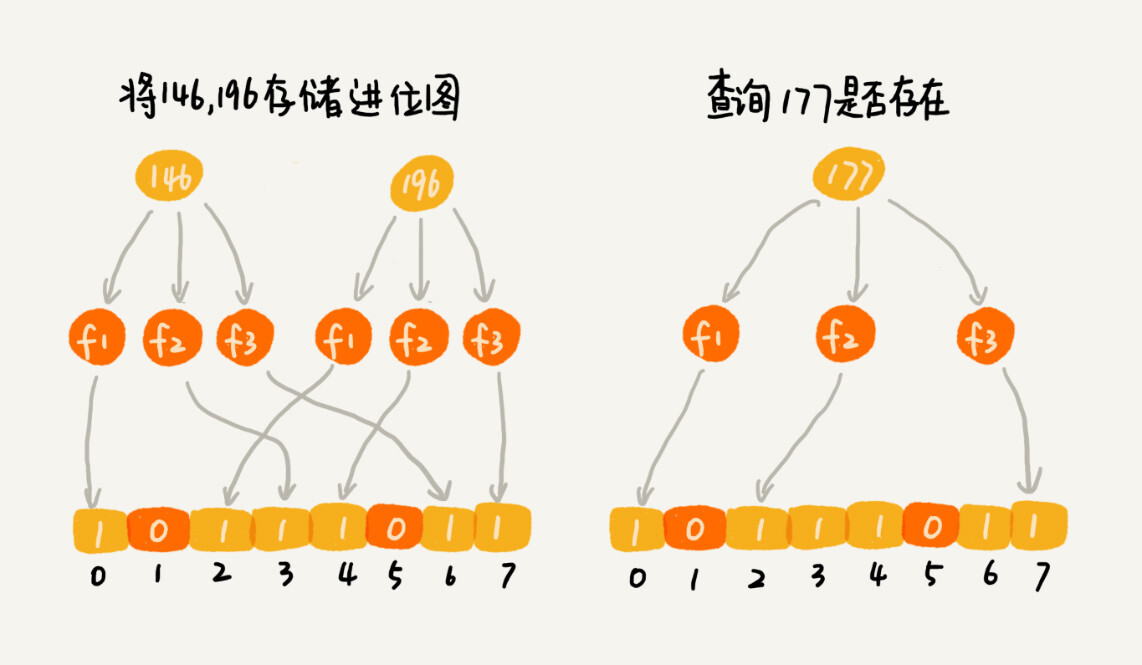
https://img.zhaoweiguo.com/knowledge/images/algorithms/bloom-filter1.jpg

备注

布隆过滤器的误判有一个特点，那就是，它只会对存在的情况有误判。如果某个数字经过布隆过滤器判断不存在，那说明这个数字真的不存在，不会发生误判；如果某个数字经过布隆过滤器判断存在，这个时候才会有可能误判，有可能并不存在。不过，只要我们调整哈希函数的个数、位图大小跟要存储数字的个数之间的比例，那就可以将这种误判的概率降到非常低。

使用场景:

爬虫: 用于记录已经爬取过的页面
    一个没有被爬取过的网页，被误判为已经被爬取，对于搜索引擎来说，也并不是什么大事情
    是可以容忍的，毕竟网页太多了，搜索引擎也不可能 100% 都爬取到
手机号黑名单: 骚扰电话号码和垃圾短信发送号码
    每个号码看作一个字符串，并且假设平均长度是 16 个字节
    存储 50 万个电话号码:
        使用散列表、二叉树等动态数据结构来存储: 大约需要 10MB 的内存空间
    要存储 500 万个手机号码:
        使用布隆过滤器存储:
        我们把位图大小设置为 10 倍数据大小，也就是 5000 万，
        需要使用 5000 万个二进制位（5000 万 bits），换算成字节，也就是不到 7MB 的存储空间
    不过:
        布隆过滤器会有判错的概率！
        如果它把一个重要的电话或者短信，当成垃圾短信或者骚扰电话拦截了，
        对于用户来说，这是无法接受的

应用:

Java 中的 BitSet 类就是一个位图
Redis 也提供了 BitMap 位图类
Google 的 Guava 工具包

概率统计

备注

贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。而朴素朴素贝叶斯分类是贝叶斯分类中最简单，也是常见的一种分类方法。

朴素贝叶斯算法:

P(A|B) = [P(B|A)]*P(A)]/P(B)

P(A|B): 在事件B 发生的前提下，事件 A 发生的概率
P(B|A): 在事件A 发生的前提下，事件 B 发生的概率
P(A): 事件 A 发生的概率
P(B): 事件 B 发生的概率

实例-垃圾短信:

P(是垃圾短信|W1,W2...Wn 同时出现在短信中)=X/Y
其中:
    X= P(W1,W2...Wn 同时出现在短信中|是垃圾短信) * P(短信是垃圾短信)
    Y = P(W1,W2...Wn 同时出现在短信中)
而:
    P(W1,W2...Wn 同时出现在短信中|是垃圾短信)=
        P(W1出现在短信中|是垃圾短信) *
        P(W2出现在短信中|是垃圾短信) *
        ...
        P(Wn出现在短信中|是垃圾短信) *
    P(W1,W2...Wn 同时出现在短信中)
        P(W1出现在短信中) *
        P(W2出现在短信中) *
        ...
        P(Wn出现在短信中) *

向量空间

歌曲推荐系统的核心思想:

找到跟你口味偏好相似的用户，把他们爱听的歌曲推荐给你
找出跟你喜爱的歌曲特征相似的歌曲，把这些歌曲推荐给你

通过用户的行为，来定义这个喜爱程度。我们给每个行为定义一个得分:

1. 跳过: -1
2. 没听过: 0
3. 听完: 1
4. 搜索: 2
5. 收藏: 3
6. 分享: 4
7. 单曲循环: 5

欧几里得距离-Euclidean distance:

用来计算两个向量之间的距离的

曼哈顿距离-Manhattan distance:

欧几里得距离的计算公式，会涉及比较耗时的开根号计算
曼哈顿距离是两点之间横纵坐标的距离之和。
计算的过程只涉及加减法、符号位反转，所以比欧几里得距离更加高效。

Math.abs(v1.x - v2.x) + Math.abs(v1.y - v2.y);

算法解析

  1. 解决问题的前提是定义清楚问题:

    除了对问题进行详细的调研，
还有就是，通过对一些模糊的需求进行假设，来限定要解决的问题的范围
    如: 限定在时间和空间两方面，也就是执行效率和存储空间
    在执行效率方面，我们希望通过索引，查询数据的效率尽可能地高；
    在存储空间方面，我们希望索引不要消耗太多的内存空间。

  2. 尝试用学过的数据结构解决这个问题:

    尝试用: 散列表、二叉树、跳表解决这个问题
B+树和跳表很像，但是通过二叉树演进过来的

  3. 改造二叉查找树来解决这个问题:

    树中的节点并不存储数据本身，而是只是作为索引
把每个叶子节点串在一条链表上，链表中的数据是从小到大有序的

区间查询:
    用区间的起始值，在树中进行查找，当查找到某个叶子节点之后，
    我们再顺着链表往后遍历，直到链表中的结点数据值大于区间的终止值为止。
    所有遍历到的数据，就是符合区间值的所有数据。

B+树

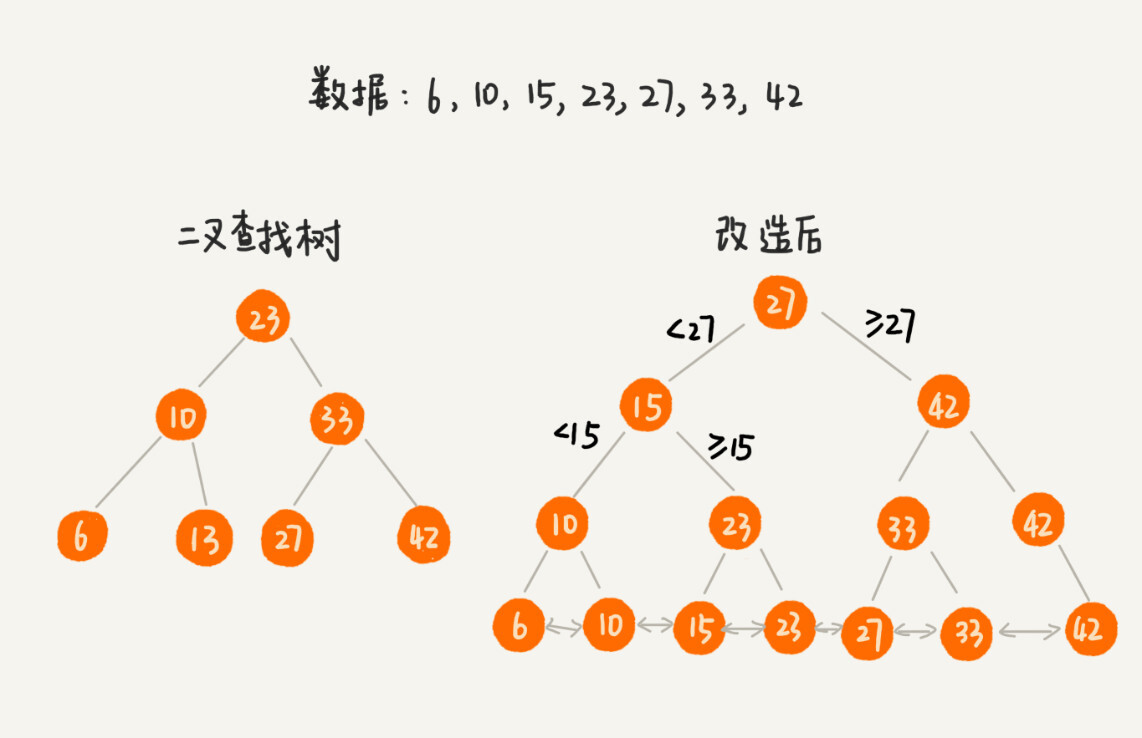
https://img.zhaoweiguo.com/knowledge/images/algorithms/tree-b+1.jpeg

把二叉树改造成 B+树

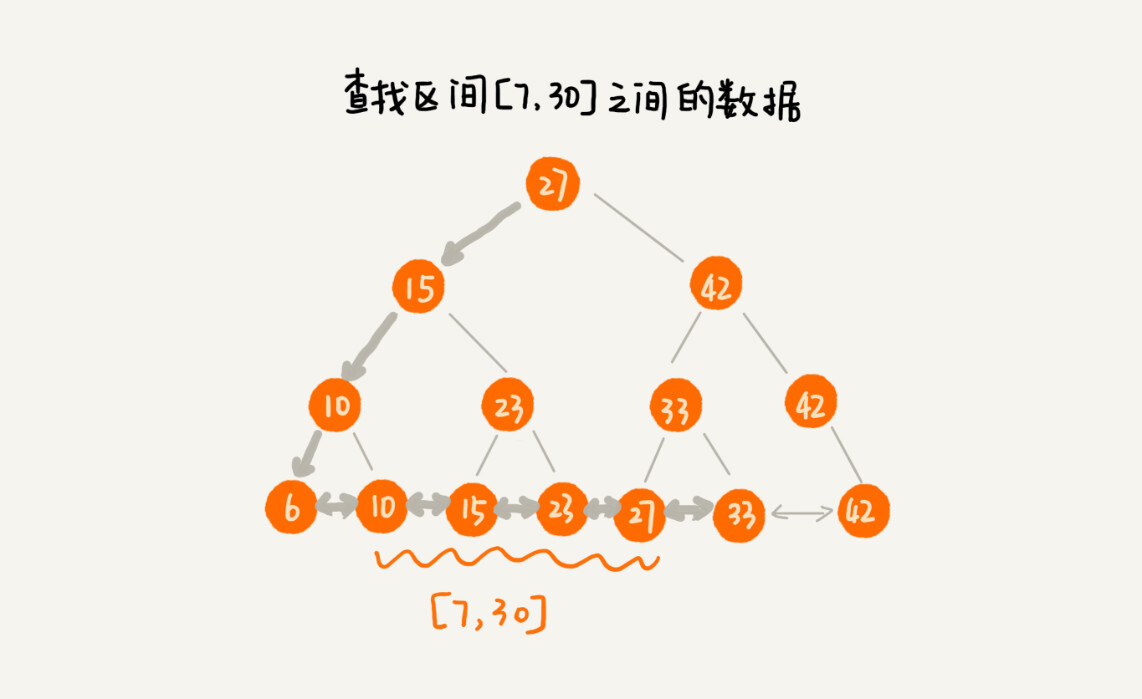
https://img.zhaoweiguo.com/knowledge/images/algorithms/tree-b+2.jpeg

区间查询

把索引放内存占用的内存会非常多:

给一亿个数据构建二叉查找树索引，那索引中会包含大约 1 亿个节点，
每个节点假设占用 16 个字节，那就需要大约 1GB 的内存空间
    给一张表建立索引，我们需要 1GB 的内存空间。如果我们要给 10 张表建立索引

借助时间换空间的思路，把索引存储在硬盘中，而非内存中。
    但硬盘是一个非常慢速的存储设备。
    通常内存的访问速度是纳秒级别的，而磁盘访问的速度是毫秒级别的。
    读取同样大小的数据，从磁盘中读取花费的时间，是从内存中读取所花费时间的上万倍，甚至几十万倍。

每个节点的读取（或者访问），都对应一次磁盘 IO 操作。
    树的高度就等于每次查询数据时磁盘 IO 操作的次数。
    优化的重点就是尽量减少磁盘 IO 操作，也就是，尽量降低树的高度
    把索引构建成 m 叉树，高度就比二叉树要小

如果 m 叉树中的 m 是 100
    那对一亿个数据构建索引，树的高度也只是 3，最多只要 3 次磁盘 IO 就能获取到数据
    磁盘 IO 变少了，查找数据的效率也就提高了

备注

我们在选择 m 大小的时候，要尽量让每个节点的大小等于一个页的大小。读取一个节点，只需要一次磁盘 IO 操作。

B+ 树的特点:

1. 每个节点中子节点的个数不能超过 m，也不能小于 m/2
2. 根节点的子节点个数可以不超过 m/2，这是一个例外
3. m 叉树只存储索引，并不真正存储数据，这个有点儿类似跳表
4. 通过链表将叶子节点串联在一起，这样可以方便按区间查找
5. 一般情况，根节点会被存储在内存中，其他节点存储在磁盘中

备注

除了 B+ 树，你可能还听说过 B 树、B- 树。B- 树就是 B 树，英文翻译都是 B-Tree，这里的“-”并不是相对 B+ 树中的“+”，而只是一个连接符，这个很容易误解。B 树实际上是低级版的 B+ 树，或者说 B+ 树是 B 树的改进版。

B 树跟 B+ 树的不同点主要集中在这几个地方:

1. B+ 树中的节点不存储数据，只是索引，而 B 树中的节点存储数据
2. B 树中的叶子节点并不需要链表来串联

也就是说，B 树只是一个每个节点的子节点个数不能小于 m/2 的 m 叉树

理解B+tree的几个要点:

1. 理解二叉查找树
2. 理解二叉查找树会出现不平衡的问题（红黑树理解了，对于平衡性这个关键点就理解了）
3. 磁盘IO访问太耗时
4. 当然，链表知识跑不了 —— 别小瞧这个简单的数据结构，它是链式结构之母
5. 最后，要知道典型的应用场景：数据库的索引结构的设计

A* 算法

  • A* 算法是对 Dijkstra 算法的优化和改造

  • Dijkstra 算法有点儿类似 BFS 算法

  • A* 算法属于一种启发式搜索算法（Heuristically Search Algorithm）:

    其他启发式搜索算法:
1. IDA* 算法
2. 蚁群算法
3. 遗传算法
4. 模拟退火算法

启发函数-heuristic function
估价函数-evaluation function

A* 算法跟 Dijkstra 算法主要有 3 点区别:

1. 优先级队列构建的方式不同。
    A* 算法是根据 f 值（ f (i)=g (i)+h (i)）来构建优先级队列，
    而 Dijkstra 算法是根据 dist 值（也就是 g (i)）来构建优先级队列；
2. A* 算法在更新顶点 dist 值的时候，会同步更新 f 值；
3. 循环结束的条件也不一样。
    Dijkstra 算法是在终点出队列的时候才结束，A* 算法是一旦遍历到终点就结束。

备注

A* 算法利用贪心算法的思路，每次都找 f 值最小的顶点出队列，一旦搜索到终点就不在继续考察其他顶点和路线了。所以，它并没有考察所有的路线，也就不可能找出最短路径了。

索引

实际的软件开发的本质都可以抽象为 “对数据的存储和计算”:

对应到数据结构和算法中:
1. “存储” 需要的就是数据结构
2. “计算” 需要的就是算法

对于存储的需求:

功能上无外乎增删改查，这其实并不复杂。
但是，一旦存储的数据很多，那性能就成了这些系统要关注的重点

如何节省存储空间、如何提高数据增删改查的执行效率，这样的问题就成了设计的重点
索引就是关键: 索引设计得好坏，直接决定了这些系统是否优秀

  1. 功能性需求:

    a. 数据是格式化数据还是非格式化数据:
    结构化数据，比如，MySQL 中的数据；
    非结构化数据，比如搜索引擎中网页。
    对于非结构化数据，我们一般需要做预处理，提取出查询关键词，对关键词构建索引。
b. 数据是静态数据还是动态数据:
    静态数据: 不会有数据的增加、删除、更新操作，
        在构建索引的时候，只需要考虑查询效率就可以了
    动态数据:
        不仅要考虑到索引的查询效率，在原始数据更新的同时，我们还需要动态地更新索引。
        支持动态数据集合的索引，设计起来相对也要更加复杂些
c. 索引存储在内存还是硬盘
    存储在内存中:
        那查询的速度肯定要比存储在磁盘中的高。
    但原始数据量很大的情况下，对应的索引可能也会很大。
        这个时候，因为内存有限，我们可能就不得不将索引存储在磁盘中了。
    第三种情况，那就是一部分存储在内存，一部分存储在磁盘
        这样就可以兼顾内存消耗和查询效率。
d. 单值查找还是区间查找
    单值查找:
        就是根据查询关键词等于某个值的数据。
    区间查找:
        就是查找关键词处于某个区间值的所有数据。
e. 单关键词查找还是多关键词组合查找
    单关键词的查找: 比如 “数据结构”
        对于单关键词的查找，索引构建起来相对简单些。
    组合关键词查找，比如 “数据结构 AND 算法”。
        对于多关键词查询来说，要分多种情况。
        像 MySQL 这种结构化数据的查询需求，我们可以实现针对多个关键词的组合，建立索引；
        像搜索引擎这样的非结构数据的查询需求，我们可以针对单个关键词构建索引，
            然后通过集合操作，比如求并集、求交集等，计算出多个关键词组合的查询结果。

  2. 非功能性需求:

    a. 不管是存储在内存中还是磁盘中，索引对存储空间的消耗不能过大
b. 在考虑索引查询效率的同时，我们还要考虑索引的维护成本

常用来构建索引的数据结构:

静态数据构建索引:
    有序数组:
        把数据的关键词（查询用的）抽取出来，组织成有序数组，然后利用二分查找算法来快速查找数据
动态数据构建索引:
    散列表:
        增删改查操作的性能非常好，时间复杂度是 O (1)
        一些键值数据库，比如 Redis、Memcache，就是使用散列表来构建索引的
        这类索引，一般都构建在内存中
    红黑树:
        数据插入、删除、查找的时间复杂度是 O (logn)，也非常适合用来构建内存索引
        Ext 文件系统中，对磁盘块的索引，用的就是红黑树
    跳表:
        支持快速添加、删除、查找数据
        通过灵活调整索引结点个数和数据个数之间的比例，可以很好地平衡索引对内存的消耗及其查询效率
        Redis 中的有序集合，就是用跳表来构建的
    B+ 树:
        相比红黑树来说，更加适合构建存储在磁盘中的索引
        B+ 树是一个多叉树，所以，对相同个数的数据构建索引，B+ 树的高度要低于红黑树
        当借助索引查询数据的时候，读取 B+ 树索引，需要的磁盘 IO 次数会更少
        所以，大部分关系型数据库的索引，比如 MySQL、Oracle，都是用 B+ 树来实现的
    trie 树:
        es 中的单排索引
        区块链拿以太坊来说吧，索引用的数据结构是帕特利夏树，一种高级的 trie 树
辅助索引:
    位图
    布隆过滤器:
        扬长避短: 内存占用非常少, 对于判定不存在的数据，那肯定就不存在
        针对数据，构建一个布隆过滤器，并且存储在内存中。
        当要查询数据的时候，我们可以先通过布隆过滤器，判定是否存在。
        如果通过布隆过滤器判定数据不存在，那我们就没有必要读取磁盘中的索引了。
        对于数据不存在的情况，数据查询就更加快速了。

并行算法

并行排序:

利用分治的思想，对数据进行分片，然后并行处理
归并排序 vs 快速排序

排序的数据规模是 1TB甚至更大时，问题的重点就不是算法的执行效率了，而是数据的读取效率
 1TB 的数据肯定是存在硬盘中，无法一次性读取到内存中，
 这样在排序的过程中，就会有频繁地磁盘数据的读取和写入。
 如何减少磁盘的 IO 操作，减少磁盘数据读取和写入的总量，就变成了优化的重点

并行查找:

散列表是一种非常适合快速查找的数据结构

将数据随机分割成 k 份（比如 16 份）
通过 16 个线程，并行地在这 16 个散列表中查找数据。

并行字符串匹配:

超级大的文本，那处理的时间可能就会变得很长
可以把大的文本，分割成 k 个小文本。假设 k 是 16，我们就启动 16 个线程，
并行地在这 16 个小文本中查找关键词，这样整个查找的性能就提高了 16 倍。

并行搜索:

搜索算法:
    1. 广度优先搜索
    2. 深度优先搜索
    3. Dijkstra 最短路径算法
    4. A* 启发式搜索算法

改造之后的并行广度优先搜索算法，我们需要利用两个队列来完成扩展顶点的工作

有 n 个任务，为提高执行的效率，并行执行任务，但是各个任务之间又有一定的依赖关系，如何根据依赖关系找出可以并行执行的任务:

用拓扑关系来构建图安排计算顺序，如:spark，tensorflow

算法实战-Redis

Redis 中，键的数据类型是字符串，但是为了丰富数据存储的方式，方便开发者使用，值的数据类型有很多，常用的数据类型有这样几种，它们分别是字符串、列表、字典、集合、有序集合。

列表-list

1. 压缩列表（ziplist）
2. 双向循环链表

1. 压缩列表-ziplist

当列表中存储的数据量比较小的时候:

1. 列表中保存的单个数据（有可能是字符串类型的）小于 64 字节
2. 列表中数据个数少于 512 个

压缩列表的好处是能利用 l2 缓存，越小越有利于 CPU 缓存
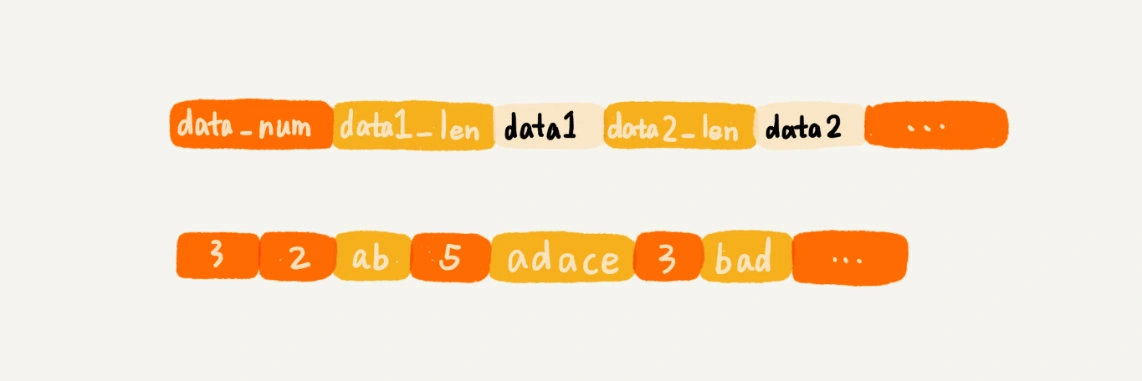
https://img.zhaoweiguo.com/knowledge/images/algorithms/redis1.webp

Redis 自己设计的一种数据存储结构——压缩列表。有点儿类似数组，通过一片连续的内存空间，来存储数据。不过，它跟数组不同的一点是，它允许存储的数据大小不同。

https://img.zhaoweiguo.com/knowledge/images/algorithms/redis1.webp

上图如果用数组设计。数组要求每个元素的大小相同，如果我们要存储不同长度的字符串，那我们就需要用最大长度的字符串大小作为元素的大小（这儿就是5字节）

备注

压缩列表这种存储结构，一方面比较节省内存，另一方面可以支持不同类型数据的存储。而且，因为数据存储在一片连续的内存空间，通过键来获取值为列表类型的数据，读取的效率也非常高。

2. 双向循环链表

备注

当列表中存储的数据量比较大时，也就是不能同时满足上面的两个条件时，列表就要通过双向循环链表来实现

备注

Redis 的这种双向链表的实现方式，非常值得借鉴。它额外定义一个 list 结构体，来组织链表的首、尾指针，还有长度等信息。这样，在使用的时候就会非常方便。

代码实现:

typedef struct listnode {
  struct listNode *prev;
  struct listNode *next;
  void *value;
} listNode;


typedef struct list {
  listNode *head;
  listNode *tail;
  unsigned long len;
  // ....省略其他定义
} list;

字典-hash

字典类型用来存储一组数据对。每个数据对又包含键值两部分。字典类型也有两种实现方式:

1. 压缩列表
    和列表一样，当存储的数据量比较小的时候使用
2. 散列表

备注

Redis 使用 MurmurHash2 <https://zh.wikipedia.org/wiki/Murmur%E5%93%88%E5%B8%8C> 这种运行速度快、随机性好的哈希算法作为哈希函数。对于哈希冲突问题，Redis 使用链表法来解决。除此之外，Redis 还支持散列表的动态扩容、缩容。

  • 当数据动态增加之后，散列表的装载因子会不停地变大。为了避免散列表性能的下降，当装载因子大于 1 的时候，Redis 会触发扩容，将散列表扩大为原来大小的 2 倍左右。

  • 当数据动态减少之后，为了节省内存，当装载因子小于 0.1 的时候，Redis 就会触发缩容，缩小为字典中数据个数的大约 2 倍大小。

  • 扩容缩容要做大量的数据搬移和哈希值的重新计算，所以比较耗时。针对这个问题，Redis 使用渐进式扩容缩容策略，将数据的搬移分批进行，避免了大量数据一次性搬移导致的服务停顿。

集合-set

集合这种数据类型用来存储一组不重复的数据。这种数据类型也有两种实现方法:

1. 基于有序数组
2. 基于散列表

同时满足这两个条件的时候，Redis 就采用有序数组，来实现:

1. 存储的数据都是整数
2. 存储的数据元素个数不超过 512 个

  • 其他情况使用「散列表」

有序集合-sortedset

当数据量比较小的时候，Redis 会用压缩列表来实现有序集合:

所有数据的大小都要小于 64 字节
元素个数要小于 128 个

  • 其他情况使用「跳表」

数据结构持久化

数据结构持久化到硬盘主要有两种解决思路:

1. 清除原有的存储结构，只将数据存储到磁盘中
    当我们需要从磁盘还原数据到内存的时候，再重新将数据组织成原来的数据结构。
    实际上，Redis 采用的就是这种持久化思路。
2. 保留原来的存储格式，将数据按照原有的格式存储在磁盘中
    以散列表这样的数据结构来举例。
    我们可以将散列表的大小、每个数据被散列到的槽的编号等信息，都保存在磁盘中。
    有了这些信息，我们从磁盘中将数据还原到内存中的时候，就可以避免重新计算哈希值。

第1种方法的弊端:

那就是数据从硬盘还原到内存的过程，会耗用比较多的时间。
如，我们现在要将散列表中的数据存储到磁盘。
当我们从磁盘中，取出数据重新构建散列表的时候，需要重新计算每个数据的哈希值。
如果磁盘中存储的是几 GB 的数据，那重构数据结构的耗时就不可忽视了

算法实战-搜索引擎

搜索引擎大致可以分为四个部分:

1. 搜集
    利用爬虫爬取网页
2. 分析
    主要负责网页内容抽取、分词，构建临时索引，计算 PageRank 值这几部分工作
3. 索引
    主要负责通过分析阶段得到的临时索引，构建倒排索引
4. 查询
    主要负责响应用户的请求，根据倒排索引获取相关网页，计算网页排名，返回查询结果给用户

搜集

基本的原理：先找一些比较知名的网页（专业的叫法是权重比较高）的链接（比如新浪主页网址、腾讯主页网址等），作为种子网页链接，放入到队列中。爬虫按照广度优先的策略，不停地从队列中取出链接，然后去爬取对应的网页，解析出网页里包含的其他网页链接，再将解析出来的链接添加到队列中

  1. 待爬取网页链接文件：links.bin:

    用一个存储在磁盘中的文件（links.bin）来作为广度优先搜索中的队列。
爬虫从 links.bin 文件中，取出链接去爬取对应的页面。
等爬取到网页之后，将解析出来的链接，直接存储到 links.bin 文件中

  2. 网页判重文件：bloom_filter.bin:

    定期地（比如每隔半小时）将布隆过滤器持久化到磁盘中，存储在 bloom_filter.bin 文件中
防止机器宕机重启之后，布隆过滤器就被清空

  3. 原始网页存储文件：doc_raw.bin:

    如果我们把每个网页都存储为一个独立的文件，那磁盘中的文件就会非常多，数量可能会有几千万，甚至上亿
所以，我们可以把多个网页存储在一个文件中。每个网页之间，通过一定的标识进行分隔，方便后续读取

存储格式如下:
网页编号    网页大小        网页    分隔符
doc1_id \t doc1_size \t doc1    \r\n\r\n
doc2_id \t doc2_size \t doc2    \r\n\r\n
...

  4. 网页链接及其编号的对应文件：doc_id.bin:

    网页编号实际上就是给每个网页分配一个唯一的 ID，方便我们后续对网页进行分析、索引

如何给网页编号:
    我们可以按照网页被爬取的先后顺序，从小到大依次编号。
具体是这样做的:
    维护一个中心的计数器，每爬取到一个网页，就从计数器中拿一个号码，分配给这个网页，然后计数器加一
    在存储网页的同时，我们将网页链接跟编号之间的对应关系，存储在另一个 doc_id.bin 文件中

分析

分析阶段主要包括两个步骤:

1. 抽取网页文本信息
2. 分词并创建临时索引

  1. 抽取网页文本信息:

    网页是半结构化数据，里面夹杂着各种标签、JavaScript 代码、CSS 样式
依靠 HTML 标签来抽取网页中的文本信息

抽取的过程，大体可以分为两步:
a. 去掉 JavaScript 代码、CSS 格式以及下拉框中的内容
b. 去掉所有 HTML 标签。这一步也是通过字符串匹配算法来实现的

  2. 分词并创建临时索引:

    对于英文网页来说，分词非常简单。我们只需要通过空格、标点符号等分隔符，将每个单词分割开来就可以了
对于中文网页来说，分词就复杂太多了。一种比较简单的思路是基于字典和规则的分词方法

每个网页的文本信息在分词完成之后，我们都得到一组单词列表。
我们把单词与网页之间的对应关系，写入到一个临时索引文件中（tmp_Index.bin）
这个临时索引文件用来构建倒排索引文件

临时索引文件的格式如下:
单词编号    分隔符     网页编号    分隔符
term1_id    \t      doc1_id     \r\n
term2_id    \t      doc2_id     \r\n
...

当所有的网页处理（分词及写入临时索引）完成之后，
我们再将这个单词跟编号之间的对应关系，写入到磁盘文件中，并命名为 term_id.bin

备注

经过分析阶段，我们得到了两个重要的文件。它们分别是临时索引文件 tmp_index.bin 和单词编号文件 term_id.bin

索引

备注

索引阶段主要负责将分析阶段产生的临时索引，构建成倒排索引。倒排索引（ Inverted index）中记录了每个单词以及包含它的网页列表。

https://img.zhaoweiguo.com/knowledge/images/algorithms/search-engine-index1.jpg

倒排索引的结构图

通过临时索引文件，构建出倒排索引文件。解决这个问题的方法有很多。考虑到临时索引文件很大，无法一次性加载到内存中，搜索引擎一般会选择使用多路归并排序的方法来实现。

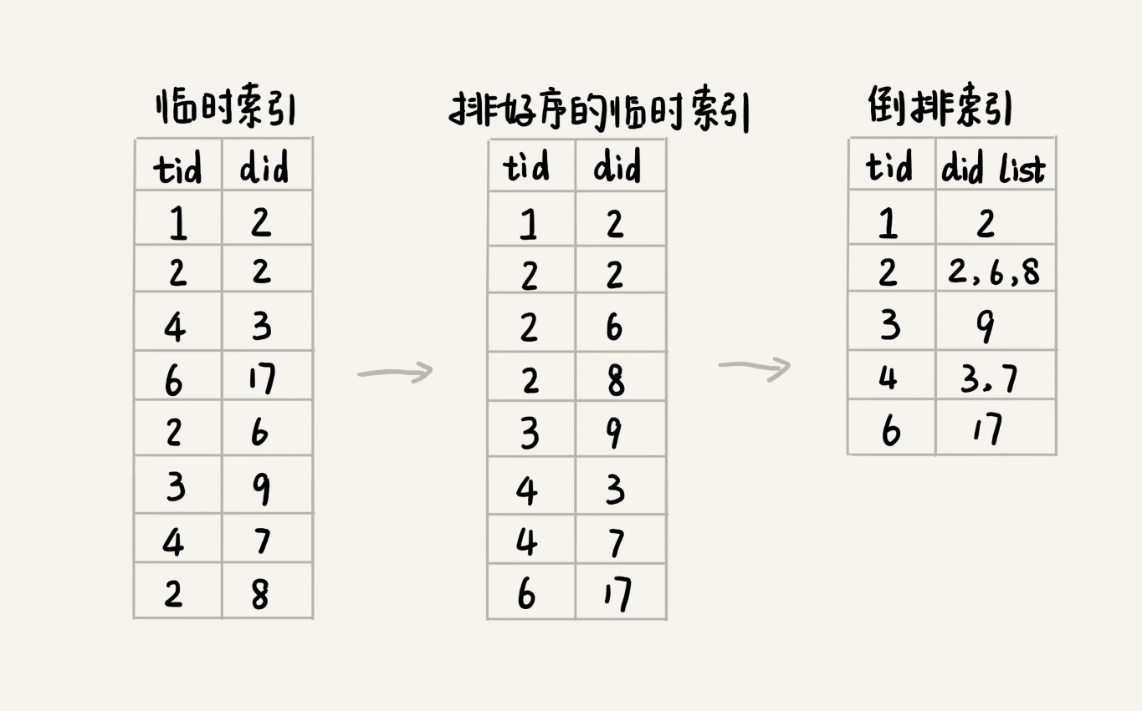
https://img.zhaoweiguo.com/knowledge/images/algorithms/search-engine-index2.jpg

临时索引文件排序完成之后，相同的单词就被排列到了一起。我们只需要顺序地遍历排好序的临时索引文件，就能将每个单词对应的网页编号列表找出来，然后把它们存储在倒排索引文件中。

  • 除了倒排文件之外，我们还需要一个文件，来记录每个单词编号在倒排索引文件中的偏移位置。我们把这个文件命名为 term_offset.bin 。这个文件的作用是，帮助我们快速地查找某个单词编号在倒排索引中存储的位置，进而快速地从倒排索引中读取单词编号对应的网页编号列表。

备注

经过索引阶段的处理，我们得到了两个有价值的文件，它们分别是倒排索引文件（index.bin）和记录单词编号在索引文件中的偏移位置的文件（term_offset.bin）

查询

要利用之前产生的几个文件，来实现最终的用户搜索功能:

1. doc_id.bin：记录网页链接和编号之间的对应关系
2. term_id.bin：记录单词和编号之间的对应关系
3. index.bin：倒排索引文件，记录每个单词编号以及对应包含它的网页编号列表
4. term_offsert.bin：记录每个单词编号在倒排索引文件中的偏移位置

备注

除了倒排索引文件（index.bin）比较大之外，其他的都比较小。为了方便快速查找数据，我们将其他三个文件都加载到内存中，并且组织成散列表这种数据结构

点击搜索时:

1. 先对用户输入的文本进行分词处理。假设分词之后，我们得到 k 个单词
2. 拿这 k 个单词，去 term_id.bin 对应的散列表中，查找对应的单词编号。
    经过这个查询之后，我们得到了这 k 个单词对应的单词编号
3. 拿这 k 个单词编号，去 term_offset.bin 的散列表中，查找每个单词编号在倒排索引文件中的偏移位置
    经过这个查询之后，我们得到了 k 个偏移位置
4. 拿这 k 个偏移位置，去倒排索引（index.bin）中，查找 k 个单词对应的包含它的网页编号列表
    经过这一步查询之后，我们得到了 k 个网页编号列表。
5. 针对这 k 个网页编号列表，统计每个网页编号出现的次数。
    具体到实现层面，我们可以借助散列表来进行统计。
    统计得到的结果，我们按照出现次数的多少，从小到大排序。
    出现次数越多，说明包含越多的用户查询单词（用户输入的搜索文本，经过分词之后的单词）。
6. 经过这一系列查询，我们就得到了一组排好序的网页编号。
    我们拿着网页编号，去 doc_id.bin 文件中查找对应的网页链接，分页显示给用户就可以了

总结

计算网页权重的PageRank算法
计算查询结果排名的tf-idf模型

涉及的数据结构和算法有:

图、散列表、Trie 树、布隆过滤器、单模式字符串匹配算法、AC 自动机、广度优先遍历、归并排序

算法实战-高性能队列 Disruptor

备注

它是一种内存消息队列。从功能上讲，它其实有点儿类似 Kafka。

队列有两种实现思路:

一种是基于链表实现的链式队列
一种是基于数组实现的顺序队列

要实现一个无界队列
    也就是说，队列的大小事先不确定，理论上可以支持无限大。
    这种情况下，我们适合选用链表来实现队列。
    因为链表支持快速地动态扩容。
要实现一个有界队列
    也就是说，队列的大小事先确定，当队列中数据满了之后，生产者就需要等待。
    直到消费者消费了数据，队列有空闲位置的时候，生产者才能将数据放入

相较于无界队列，有界队列的应用场景更加广泛。
毕竟，我们的机器内存是有限的。而无界队列占用的内存数量是不可控的

备注

非循环的顺序队列在添加、删除数据的工程中，会涉及数据的搬移操作，导致性能变差。而循环队列正好可以解决这个数据搬移的问题，所以，性能更加好。所以，大部分用到顺序队列的场景中，我们都选择用顺序队列中的循环队列。

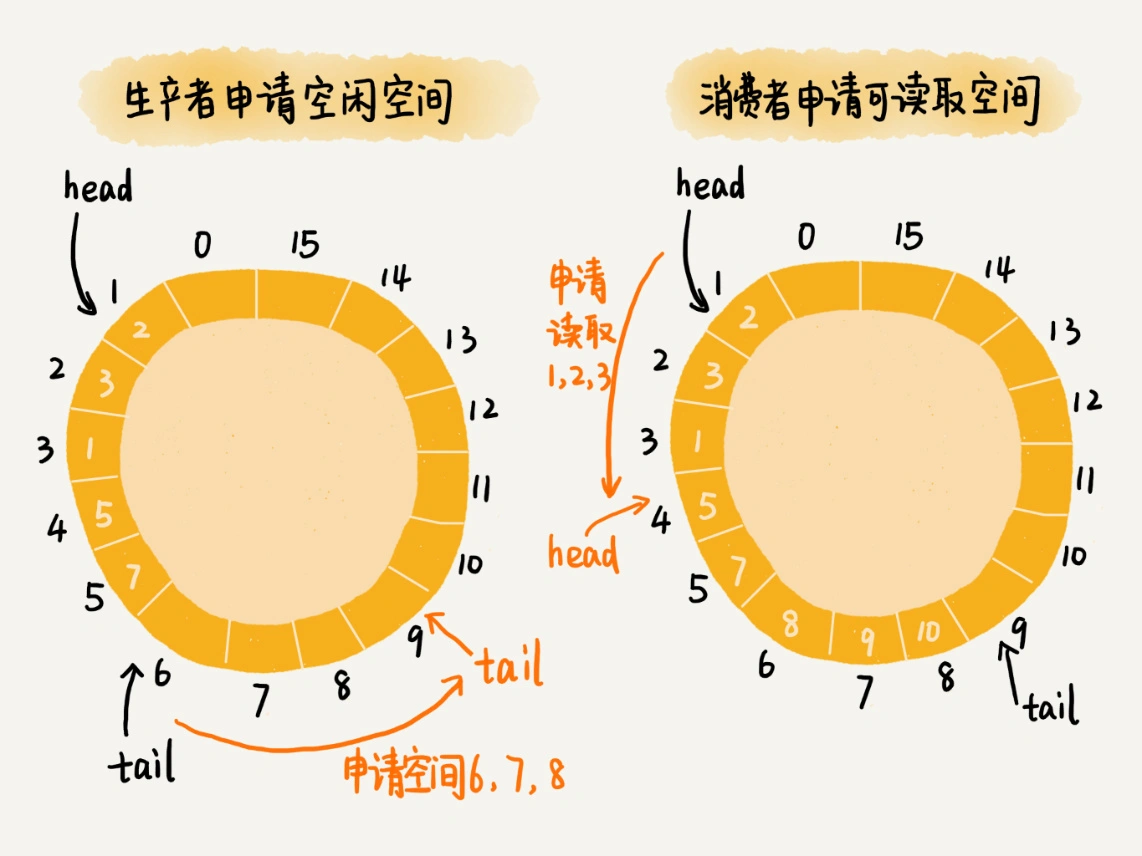
https://img.zhaoweiguo.com/knowledge/images/algorithms/circular-queue1.jpg

基于无锁的并发 “生产者 - 消费者模型”: 对于生产者来说，它往队列中添加数据之前，先申请可用空闲存储单元，并且是批量地申请连续的 n 个（n≥1）存储单元。当申请到这组连续的存储单元之后，后续往队列中添加元素，就可以不用加锁了，因为这组存储单元是这个线程独享的。

算法实战-鉴权

1. 如何实现精确匹配规则

规则不会经常变动，
所以，为加快匹配速度，可以按字符串的大小给规则排序，组织成有序数组这种数据结构
二分查找算法的时间复杂度是 O (logn)（n 表示规则的个数）

匹配的算法:
    KMP、BM、BF
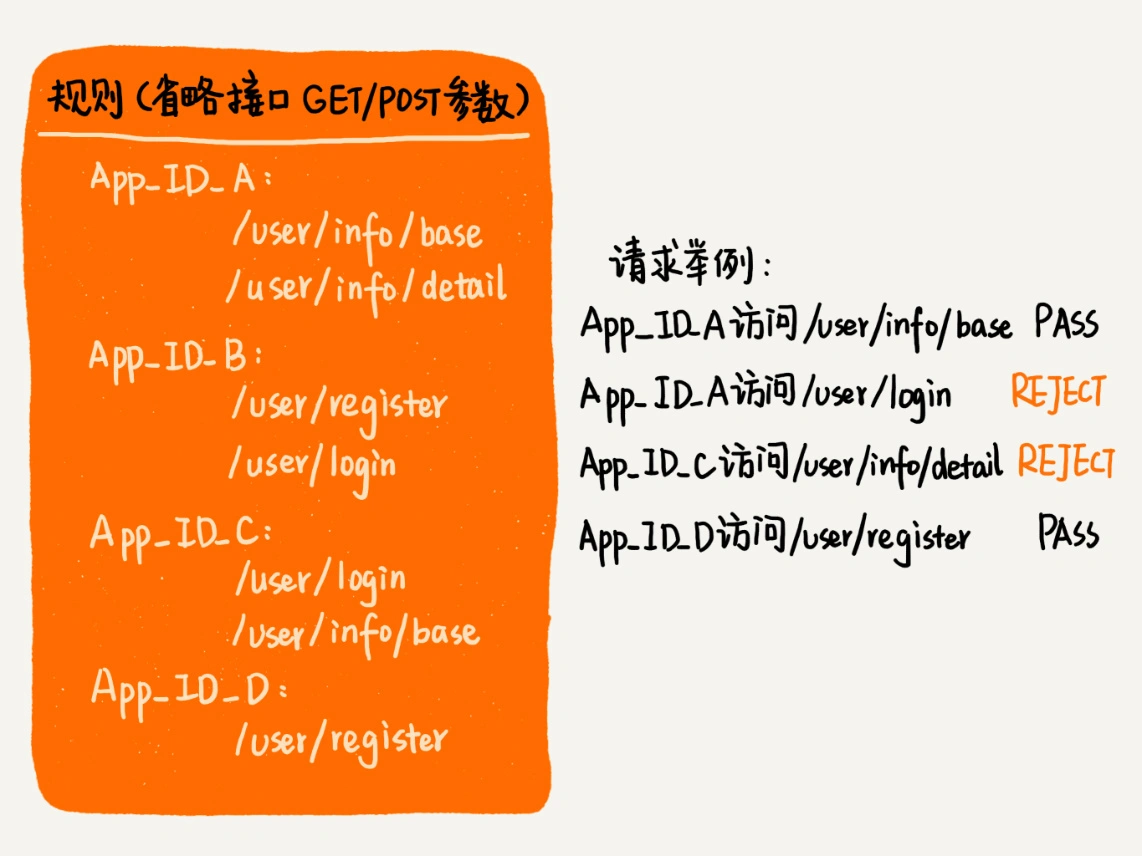
https://img.zhaoweiguo.com/knowledge/images/algorithms/authentication1.webp

2. 如何实现前缀匹配规则

不同的应用对应不同的规则集合。我们采用散列表来存储这种对应关系
每个应用的规则集合，最适合用 Trie 树来做前缀匹配
https://img.zhaoweiguo.com/knowledge/images/algorithms/authentication2.webp
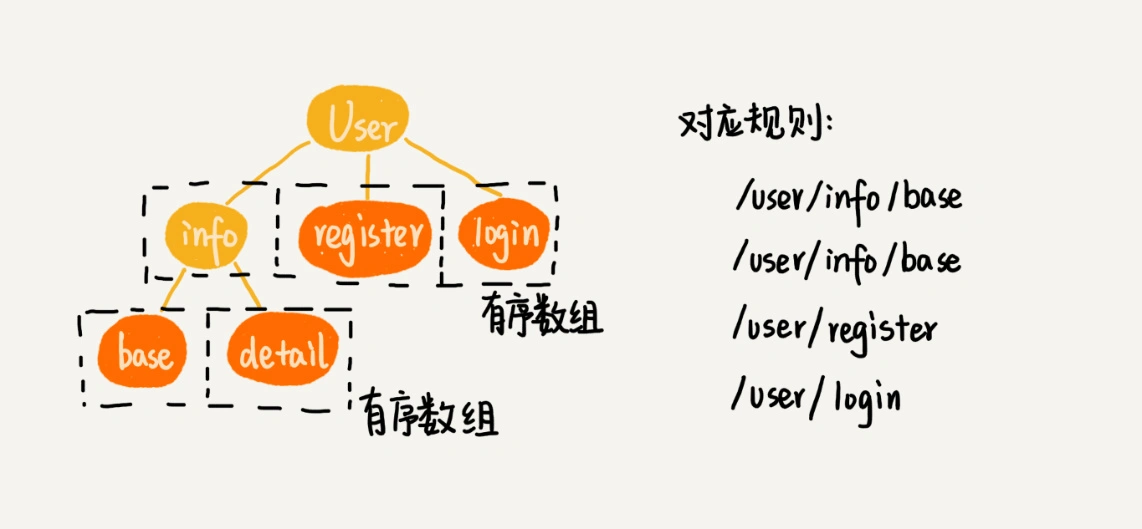
https://img.zhaoweiguo.com/knowledge/images/algorithms/authentication3.webp

在 Trie 树中，我们可以把每个节点的子节点们，组织成有序数组这种数据结构。在匹配的过程中，我们可以利用二分查找算法，决定从一个节点应该跳到哪一个子节点。

3. 如何实现模糊匹配规则

规则中包含通配符，比如:
    “**” 表示匹配任意多个子目录
    “*” 表示匹配任意一个子目录

算法:

回溯算法

技巧:

把不包含通配符的规则，组织成有序数组或者 Trie 树
剩下的是少数包含通配符的规则，我们只要把它们简单存储在一个数组中


当接收到一个请求 URL 之后:
我们可以先在不包含通配符的有序数组或者 Trie 树中查找
如果能够匹配，就不需要继续在通配符规则中匹配了
如果不能匹配，就继续在通配符规则中查找匹配

算法实战-限流

备注

限流已经成为了保证系统平稳运行的一种标配的技术解决方案。

限流算法:

1. 固定时间窗口限流算法
2. 滑动时间窗口限流算法
3. 令牌桶算法
4. 漏桶算法
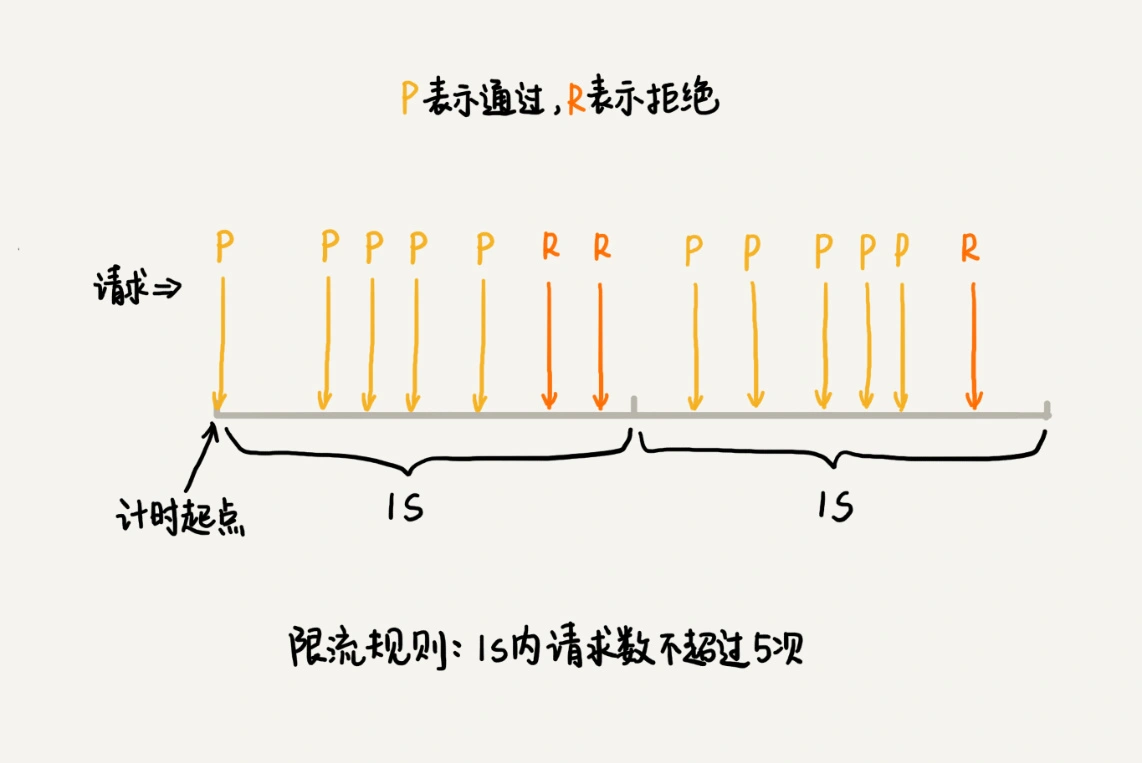
https://img.zhaoweiguo.com/knowledge/images/algorithms/throttling1.webp

1.固定时间窗口限流算法

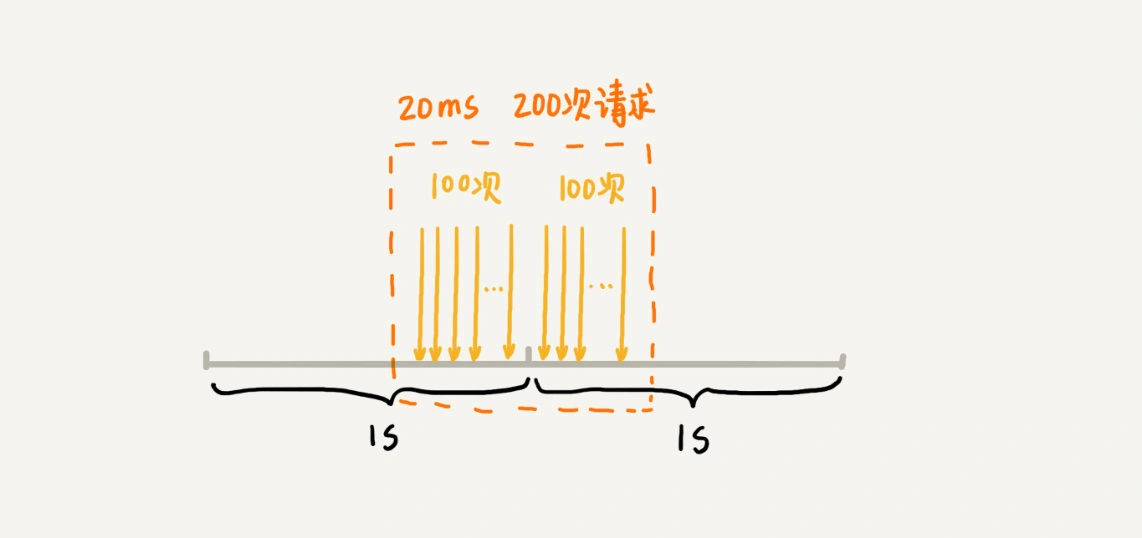
https://img.zhaoweiguo.com/knowledge/images/algorithms/throttling2.webp

固定时间窗口限流算法的问题

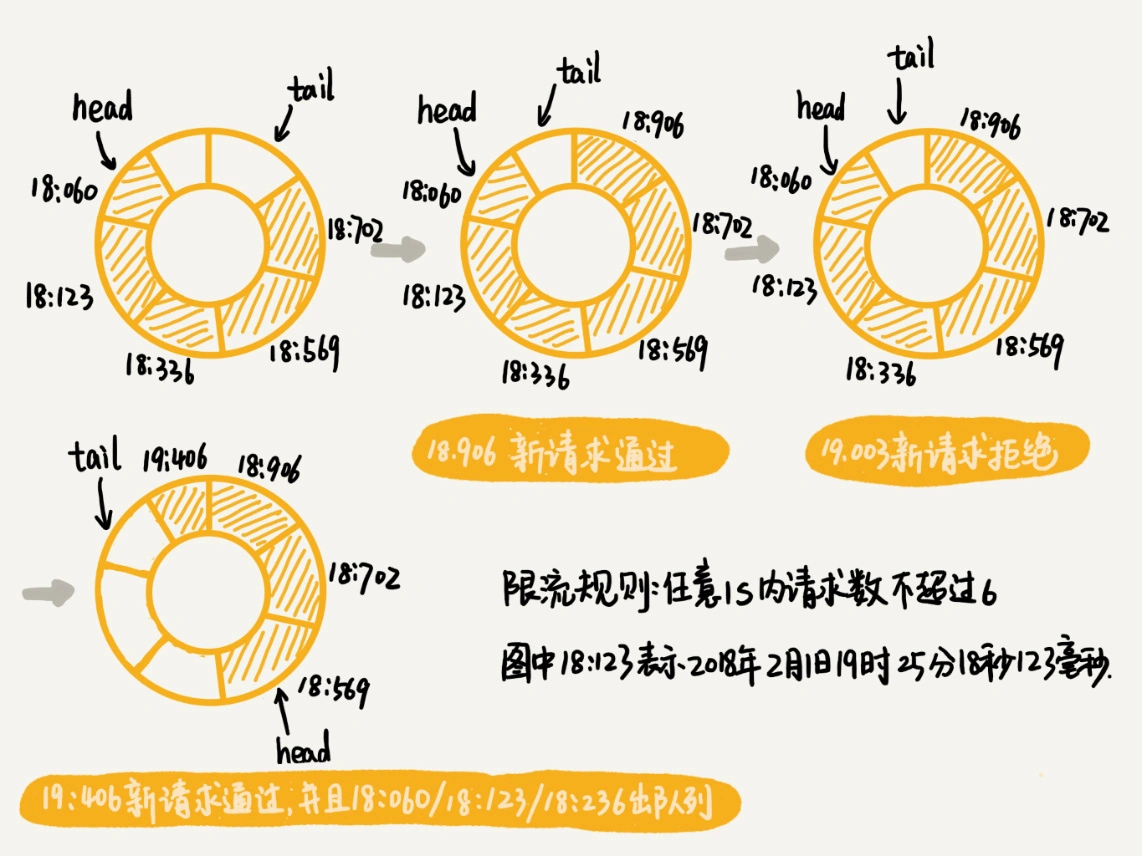
https://img.zhaoweiguo.com/knowledge/images/algorithms/throttling3.webp

2.滑动时间窗口限流算法

短网址

MurmurHash 算法:

这个哈希算法在 2008 年才被发明出来
但现在它已经广泛应用到众多著名的软件中:
 Redis、MemCache、Cassandra、HBase、Lucene

测验

必知必会的代码实现:

数组
实现一个支持动态扩容的数组
实现一个大小固定的有序数组，支持动态增删改操作
实现两个有序数组合并为一个有序数组

链表
实现单链表、循环链表、双向链表，支持增删操作实现
单链表反转
实现两个有序的链表合并为一个有序链表
实现求链表的中间结点

栈
用数组实现一个顺序栈
用链表实现一个链式栈
编程模拟实现一个浏览器的前进、后退功能

队列
用数组实现一个顺序队列
用链表实现一个链式队列
实现一个循环队列

递归
编程实现斐波那契数列求值 f(n)=f(n-1)+f(n-2)
编程实现求阶乘 n!
编程实现一组数据集合的全排列

排序
实现归并排序、快速排序、插入排序、冒泡排序、选择排序
编程实现 O(n) 时间复杂度内找到一组数据的第 K 大元素

二分查找
实现一个有序数组的二分查找算法
实现模糊二分查找算法（比如大于等于给定值的第一个元素）

散列表
实现一个基于链表法解决冲突问题的散列表
实现一个 LRU 缓存淘汰算法

字符串
实现一个字符集，只包含 a～z 这 26 个英文字母的 Trie 树
实现朴素的字符串匹配算法

二叉树
实现一个二叉查找树，并且支持插入、删除、查找操作
实现查找二叉查找树中某个节点的后继、前驱节点
实现二叉树前、中、后序以及按层遍历

堆
实现一个小顶堆、大顶堆、优先级队列
实现堆排序
利用优先级队列合并 K 个有序数组
求一组动态数据集合的最大 Top K

图
实现有向图、无向图、有权图、无权图的邻接矩阵和邻接表表示方法
实现图的深度优先搜索、广度优先搜索
实现 Dijkstra 算法、A* 算法
实现拓扑排序的 Kahn 算法、DFS 算法

回溯
利用回溯算法求解八皇后问题
利用回溯算法求解 0-1 背包问题

分治
利用分治算法求一组数据的逆序对个数

动态规划
0-1 背包问题
最小路径和（详细可看 @Smallfly 整理的 Minimum Path Sum）
编程实现莱文斯坦最短编辑距离
编程实现查找两个字符串的最长公共子序列
编程实现一个数据序列的最长递增子序列

栈

Valid Parentheses（有效的括号） 英文版：https://leetcode.com/problems/valid-parentheses/ 中文版：https://leetcode-cn.com/problems/valid-parentheses/ Longest Valid Parentheses（最长有效的括号） 英文版：https://leetcode.com/problems/longest-valid-parentheses/ 中文版：https://leetcode-cn.com/problems/longest-valid-parentheses/ Evaluate Reverse Polish Notatio（逆波兰表达式求值） 英文版：https://leetcode.com/problems/evaluate-reverse-polish-notation/ 中文版：https://leetcode-cn.com/problems/evaluate-reverse-polish-notation/

队列

Design Circular Deque（设计一个双端队列） 英文版：https://leetcode.com/problems/design-circular-deque/ 中文版：https://leetcode-cn.com/problems/design-circular-deque/ Sliding Window Maximum（滑动窗口最大值） 英文版：https://leetcode.com/problems/sliding-window-maximum/ 中文版：https://leetcode-cn.com/problems/sliding-window-maximum/

递归

Climbing Stairs（爬楼梯） 英文版：https://leetcode.com/problems/climbing-stairs/ 中文版：https://leetcode-cn.com/problems/climbing-stairs/

排序&二分查找

Sqrt (x) （x 的平方根） 英文版：https://leetcode.com/problems/sqrtx/ 中文版：https://leetcode-cn.com/problems/sqrtx/

字符串

Reverse String （反转字符串） 英文版：https://leetcode.com/problems/reverse-string/ 中文版：https://leetcode-cn.com/problems/reverse-string/ Reverse Words in a String（翻转字符串里的单词） 英文版：https://leetcode.com/problems/reverse-words-in-a-string/ 中文版：https://leetcode-cn.com/problems/reverse-words-in-a-string/ String to Integer (atoi)（字符串转换整数 (atoi)） 英文版：https://leetcode.com/problems/string-to-integer-atoi/ 中文版：https://leetcode-cn.com/problems/string-to-integer-atoi/

二叉树

Invert Binary Tree（翻转二叉树） 英文版：https://leetcode.com/problems/invert-binary-tree/ 中文版：https://leetcode-cn.com/problems/invert-binary-tree/ Maximum Depth of Binary Tree（二叉树的最大深度） 英文版：https://leetcode.com/problems/maximum-depth-of-binary-tree/ 中文版：https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/ Validate Binary Search Tree（验证二叉查找树） 英文版：https://leetcode.com/problems/validate-binary-search-tree/ 中文版：https://leetcode-cn.com/problems/validate-binary-search-tree/ Path Sum（路径总和） 英文版：https://leetcode.com/problems/path-sum/ 中文版：https://leetcode-cn.com/problems/path-sum/

图

Number of Islands（岛屿的个数） 英文版：https://leetcode.com/problems/number-of-islands/description/ 中文版：https://leetcode-cn.com/problems/number-of-islands/description/Valid Sudoku（有效的数独） 英文版：https://leetcode.com/problems/valid-sudoku/

回溯&动态规划

Regular Expression Matching（正则表达式匹配） 英文版：https://leetcode.com/problems/regular-expression-matching/ 中文版：https://leetcode-cn.com/problems/regular-expression-matching/ Minimum Path Sum（最小路径和） 英文版：https://leetcode.com/problems/minimum-path-sum/ 中文版：https://leetcode-cn.com/problems/minimum-path-sum/ Coin Change （零钱兑换） 英文版：https://leetcode.com/problems/coin-change/ 中文版：https://leetcode-cn.com/problems/coin-change/ Best Time to Buy and Sell Stock（买卖股票的最佳时机） 英文版：https://leetcode.com/problems/best-time-to-buy-and-sell-stock/ 中文版：https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock/ Maximum Product Subarray（乘积最大子序列） 英文版：https://leetcode.com/problems/maximum-product-subarray/ 中文版：https://leetcode-cn.com/problems/maximum-product-subarray/ Triangle（三角形最小路径和） 英文版：https://leetcode.com/problems/triangle/ 中文版：https://leetcode-cn.com/problems/triangle/

总结

怎么才算真正掌握了一个数据结构或算法

备注

不管是基础数据结构和算法，还是高级数据结构和算法，我们更侧重掌握它的特点、时间空间复杂度、能解决的问题、应用场景。毕竟掌握了这些之后，我们就可以在实际的开发中，遇到相应的问题或者场景，能快速的反映出，可以用哪种数据结构和算法解决。对原理或者代码实现，即便你可能已经记忆不清楚了，但也可以通过重温一遍，快速的掌握。

基础的部分:

1. 结构: 链表、数组、队列、栈、二叉树、堆、图的定义
2. 算法: 排序、二分查找、二叉树的遍历、图的广度、深度优先搜索、字符串朴素匹配算法，
3. 算法思想: 递归、分治、贪心、回溯、动态规划

参考

临时

主页

索引

模块索引

搜索页面